Is Data Valuation Learnable and Interpretable?

Measuring the value of individual samples is critical for many data-driven tasks, e.g., the training of a deep learning model. Recent literature witnesses the substantial efforts in developing data valuation methods. The primary data valuation methodology is based on the Shapley value from game theory, and various methods are proposed along this path. {Even though Shapley value-based valuation has solid theoretical basis, it is entirely an experiment-based approach and no valuation model has been constructed so far.} In addition, current data valuation methods ignore the interpretability of the output values, despite an interptable data valuation method is of great helpful for applications such as data pricing. This study aims to answer an important question: is data valuation learnable and interpretable? A learned valuation model have several desirable merits such as fixed number of parameters and knowledge reusability. An intrepretable data valuation model can explain why a sample is valuable or invaluable. To this end, two new data value modeling frameworks are proposed, in which a multi-layer perception~(MLP) and a new regression tree are utilized as specific base models for model training and interpretability, respectively. Extensive experiments are conducted on benchmark datasets. {The experimental results provide a positive answer for the question.} Our study opens up a new technical path for the assessing of data values. Large data valuation models can be built across many different data-driven tasks, which can promote the widespread application of data valuation.

Understanding Difficulty-based Sample Weighting with a Universal Difficulty Measure

Sample weighting is widely used in deep learning. A large number of weighting methods essentially utilize the learning difficulty of training samples to calculate their weights. In this study, this scheme is called difficulty-based weighting. Two important issues arise when explaining this scheme. First, a unified difficulty measure that can be theoretically guaranteed for training samples does not exist. The learning difficulties of the samples are determined by multiple factors including noise level, imbalance degree, margin, and uncertainty. Nevertheless, existing measures only consider a single factor or in part, but not in their entirety. Second, a comprehensive theoretical explanation is lacking with respect to demonstrating why difficulty-based weighting schemes are effective in deep learning. In this study, we theoretically prove that the generalization error of a sample can be used as a universal difficulty measure. Furthermore, we provide formal theoretical justifications on the role of difficulty-based weighting for deep learning, consequently revealing its positive influences on both the optimization dynamics and generalization performance of deep models, which is instructive to existing weighting schemes.

Exploring the Learning Difficulty of Data Theory and Measure

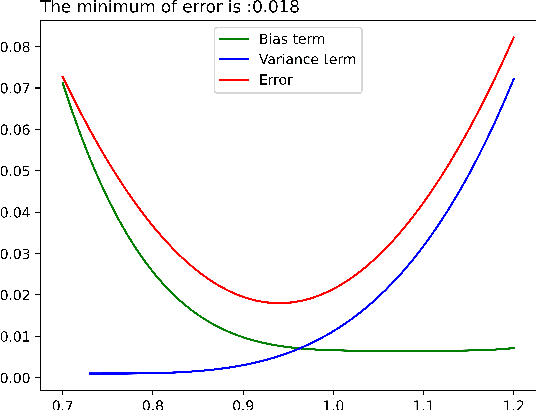
As learning difficulty is crucial for machine learning (e.g., difficulty-based weighting learning strategies), previous literature has proposed a number of learning difficulty measures. However, no comprehensive investigation for learning difficulty is available to date, resulting in that nearly all existing measures are heuristically defined without a rigorous theoretical foundation. In addition, there is no formal definition of easy and hard samples even though they are crucial in many studies. This study attempts to conduct a pilot theoretical study for learning difficulty of samples. First, a theoretical definition of learning difficulty is proposed on the basis of the bias-variance trade-off theory on generalization error. Theoretical definitions of easy and hard samples are established on the basis of the proposed definition. A practical measure of learning difficulty is given as well inspired by the formal definition. Second, the properties for learning difficulty-based weighting strategies are explored. Subsequently, several classical weighting methods in machine learning can be well explained on account of explored properties. Third, the proposed measure is evaluated to verify its reasonability and superiority in terms of several main difficulty factors. The comparison in these experiments indicates that the proposed measure significantly outperforms the other measures throughout the experiments.

A Mathematical Foundation for Robust Machine Learning based on Bias-Variance Trade-off

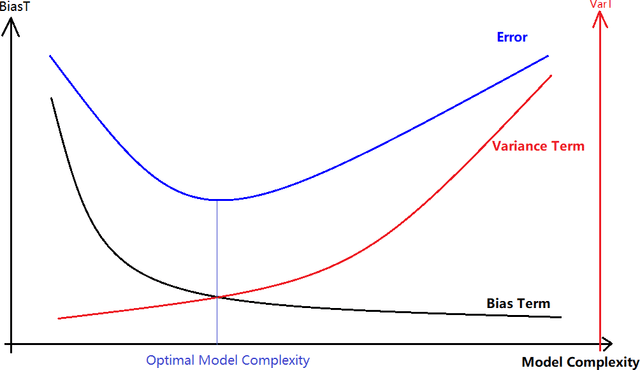
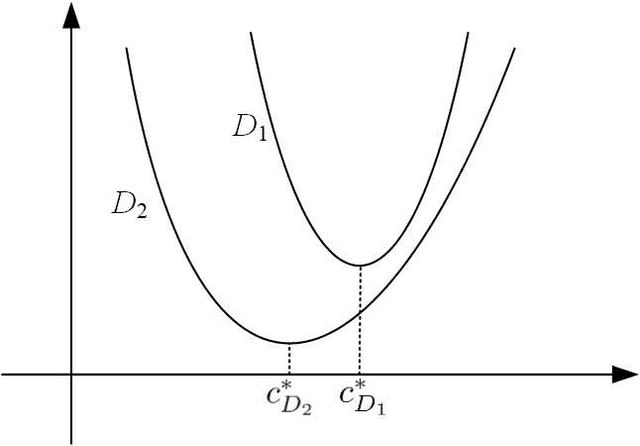
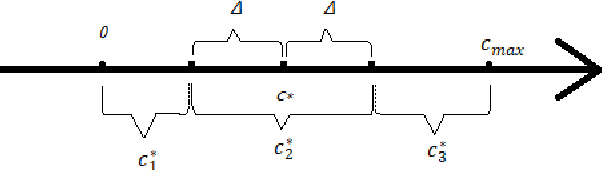
A common assumption in machine learning is that samples are independently and identically distributed (i.i.d). However, the contributions of different samples are not identical in training. Some samples are difficult to learn and some samples are noisy. The unequal contributions of samples has a considerable effect on training performances. Studies focusing on unequal sample contributions (e.g., easy, hard, noisy) in learning usually refer to these contributions as robust machine learning (RML). Weighing and regularization are two common techniques in RML. Numerous learning algorithms have been proposed but the strategies for dealing with easy/hard/noisy samples differ or even contradict with different learning algorithms. For example, some strategies take the hard samples first, whereas some strategies take easy first. Conducting a clear comparison for existing RML algorithms in dealing with different samples is difficult due to lack of a unified theoretical framework for RML. This study attempts to construct a mathematical foundation for RML based on the bias-variance trade-off theory. A series of definitions and properties are presented and proved. Several classical learning algorithms are also explained and compared. Improvements of existing methods are obtained based on the comparison. A unified method that combines two classical learning strategies is proposed.