Generalized probabilistic canonical correlation analysis for multi-modal data integration with full or partial observations

Background: The integration and analysis of multi-modal data are increasingly essential across various domains including bioinformatics. As the volume and complexity of such data grow, there is a pressing need for computational models that not only integrate diverse modalities but also leverage their complementary information to improve clustering accuracy and insights, especially when dealing with partial observations with missing data. Results: We propose Generalized Probabilistic Canonical Correlation Analysis (GPCCA), an unsupervised method for the integration and joint dimensionality reduction of multi-modal data. GPCCA addresses key challenges in multi-modal data analysis by handling missing values within the model, enabling the integration of more than two modalities, and identifying informative features while accounting for correlations within individual modalities. The model demonstrates robustness to various missing data patterns and provides low-dimensional embeddings that facilitate downstream clustering and analysis. In a range of simulation settings, GPCCA outperforms existing methods in capturing essential patterns across modalities. Additionally, we demonstrate its applicability to multi-omics data from TCGA cancer datasets and a multi-view image dataset. Conclusion: GPCCA offers a useful framework for multi-modal data integration, effectively handling missing data and providing informative low-dimensional embeddings. Its performance across cancer genomics and multi-view image data highlights its robustness and potential for broad application. To make the method accessible to the wider research community, we have released an R package, GPCCA, which is available at https://github.com/Kaversoniano/GPCCA.

Bridging Cost-sensitive and Neyman-Pearson Paradigms for Asymmetric Binary Classification

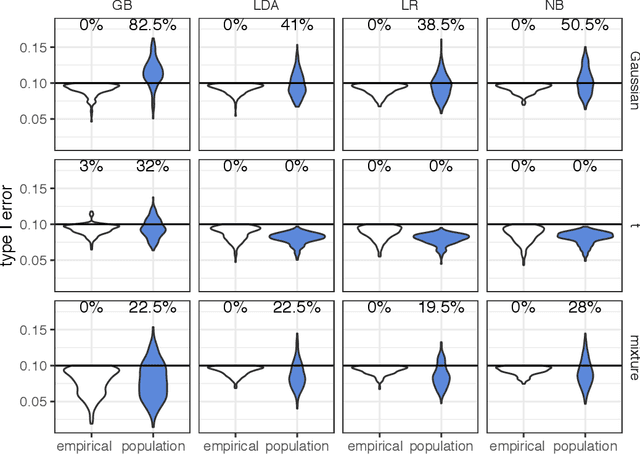
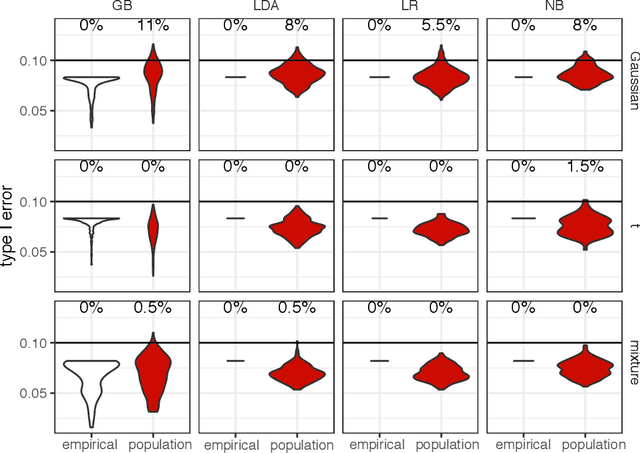
Asymmetric binary classification problems, in which the type I and II errors have unequal severity, are ubiquitous in real-world applications. To handle such asymmetry, researchers have developed the cost-sensitive and Neyman-Pearson paradigms for training classifiers to control the more severe type of classification error, say the type I error. The cost-sensitive paradigm is widely used and has straightforward implementations that do not require sample splitting; however, it demands an explicit specification of the costs of the type I and II errors, and an open question is what specification can guarantee a high-probability control on the population type I error. In contrast, the Neyman-Pearson paradigm can train classifiers to achieve a high-probability control of the population type I error, but it relies on sample splitting that reduces the effective training sample size. Since the two paradigms have complementary strengths, it is reasonable to combine their strengths for classifier construction. In this work, we for the first time study the methodological connections between the two paradigms, and we develop the TUBE-CS algorithm to bridge the two paradigms from the perspective of controlling the population type I error.