W. D. Brinda
Estimating the Coefficients of a Mixture of Two Linear Regressions by Expectation Maximization
Oct 16, 2018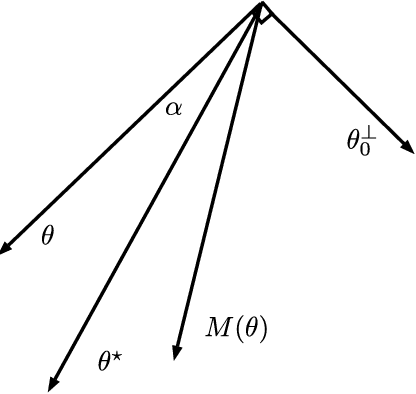
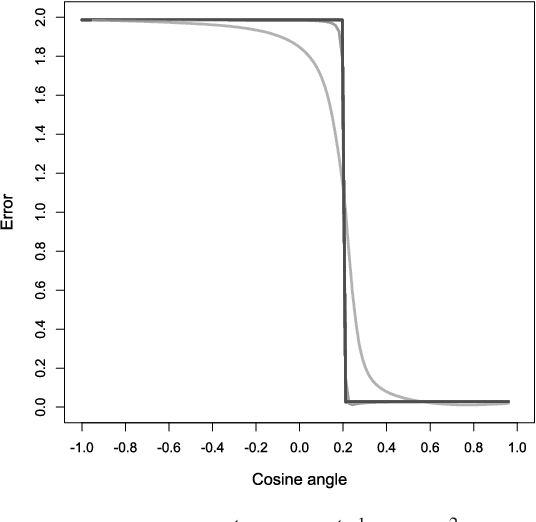
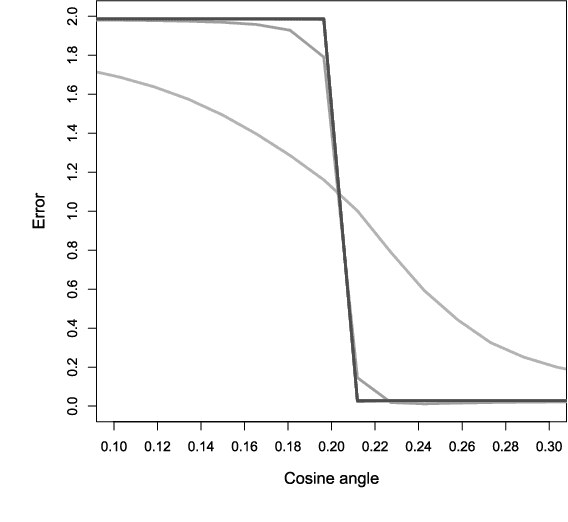
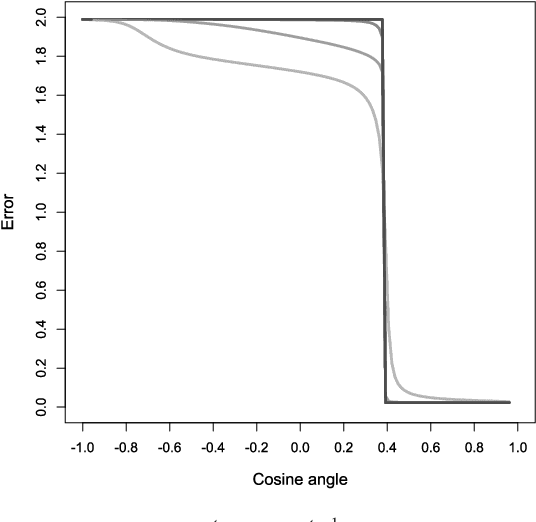
Abstract:We give convergence guarantees for estimating the coefficients of a symmetric mixture of two linear regressions by expectation maximization (EM). In particular, we show that the empirical EM iterates converge to the target parameter vector at the parametric rate, provided the algorithm is initialized in an unbounded cone. In particular, if the initial guess has a sufficiently large cosine angle with the target parameter vector, a sample-splitting version of the EM algorithm converges to the true coefficient vector with high probability. Interestingly, our analysis borrows from tools used in the problem of estimating the centers of a symmetric mixture of two Gaussians by EM. We also show that the population EM operator for mixtures of two regressions is anti-contractive from the target parameter vector if the cosine angle between the input vector and the target parameter vector is too small, thereby establishing the necessity of our conic condition. Finally, we give empirical evidence supporting this theoretical observation, which suggests that the sample based EM algorithm performs poorly when initial guesses are drawn accordingly. Our simulation study also suggests that the EM algorithm performs well even under model misspecification (i.e., when the covariate and error distributions violate the model assumptions).
Finite-sample risk bounds for maximum likelihood estimation with arbitrary penalties
Dec 29, 2017Abstract:The MDL two-part coding $ \textit{index of resolvability} $ provides a finite-sample upper bound on the statistical risk of penalized likelihood estimators over countable models. However, the bound does not apply to unpenalized maximum likelihood estimation or procedures with exceedingly small penalties. In this paper, we point out a more general inequality that holds for arbitrary penalties. In addition, this approach makes it possible to derive exact risk bounds of order $1/n$ for iid parametric models, which improves on the order $(\log n)/n$ resolvability bounds. We conclude by discussing implications for adaptive estimation.
Statistical Guarantees for Estimating the Centers of a Two-component Gaussian Mixture by EM
Aug 07, 2016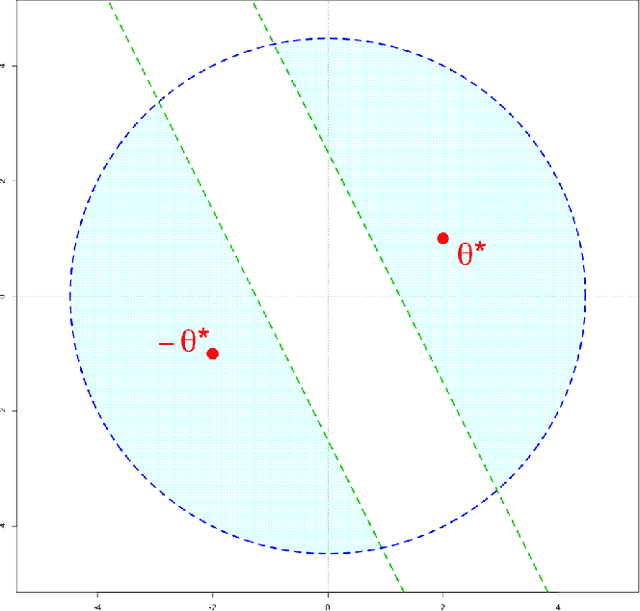
Abstract:Recently, a general method for analyzing the statistical accuracy of the EM algorithm has been developed and applied to some simple latent variable models [Balakrishnan et al. 2016]. In that method, the basin of attraction for valid initialization is required to be a ball around the truth. Using Stein's Lemma, we extend these results in the case of estimating the centers of a two-component Gaussian mixture in $d$ dimensions. In particular, we significantly expand the basin of attraction to be the intersection of a half space and a ball around the origin. If the signal-to-noise ratio is at least a constant multiple of $ \sqrt{d\log d} $, we show that a random initialization strategy is feasible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge