Volker Roth
University of Basel
NIMO: a Nonlinear Interpretable MOdel
Jun 05, 2025Abstract:Neural networks (NNs) have achieved tremendous success over the past decade, yet they are still extremely difficult to interpret. In contrast, linear models are less expressive but offer inherent interpretability. Linear coefficients are interpretable as the marginal effect of a feature on the prediction, assuming all other features are kept fixed. To combine the benefits of both approaches, we introduce NIMO (Nonlinear Interpretable MOdel). The key idea is to define a model where the NN is designed to learn nonlinear corrections to the linear model predictions, while also maintaining the original interpretability of the linear coefficients. Relevantly, we develop an optimization algorithm based on profile likelihood that elegantly allows for optimizing over the NN parameters while updating the linear coefficients analytically. By relying on adaptive ridge regression we can easily incorporate sparsity constraints as well. We show empirically that we can recover the underlying linear coefficients while significantly improving the predictive accuracy. Compared to other hybrid interpretable approaches, our model is the only one that actually maintains the same interpretability of linear coefficients as in linear models. We also achieve higher performance on various regression and classification settings.
Injective Flows for parametric hypersurfaces
Jun 13, 2024



Abstract:Normalizing Flows (NFs) are powerful and efficient models for density estimation. When modeling densities on manifolds, NFs can be generalized to injective flows but the Jacobian determinant becomes computationally prohibitive. Current approaches either consider bounds on the log-likelihood or rely on some approximations of the Jacobian determinant. In contrast, we propose injective flows for parametric hypersurfaces and show that for such manifolds we can compute the Jacobian determinant exactly and efficiently, with the same cost as NFs. Furthermore, we show that for the subclass of star-like manifolds we can extend the proposed framework to always allow for a Cartesian representation of the density. We showcase the relevance of modeling densities on hypersurfaces in two settings. Firstly, we introduce a novel Objective Bayesian approach to penalized likelihood models by interpreting level-sets of the penalty as star-like manifolds. Secondly, we consider Bayesian mixture models and introduce a general method for variational inference by defining the posterior of mixture weights on the probability simplex.
Physics-Informed Boundary Integral Networks (PIBI-Nets): A Data-Driven Approach for Solving Partial Differential Equations
Aug 18, 2023Abstract:Partial differential equations (PDEs) can describe many relevant phenomena in dynamical systems. In real-world applications, we commonly need to combine formal PDE models with (potentially noisy) observations. This is especially relevant in settings where we lack information about boundary or initial conditions, or where we need to identify unknown model parameters. In recent years, Physics-informed neural networks (PINNs) have become a popular tool for problems of this kind. In high-dimensional settings, however, PINNs often suffer from computational problems because they usually require dense collocation points over the entire computational domain. To address this problem, we present Physics-Informed Boundary Integral Networks (PIBI-Nets) as a data-driven approach for solving PDEs in one dimension less than the original problem space. PIBI-Nets only need collocation points at the computational domain boundary, while still achieving highly accurate results, and in several practical settings, they clearly outperform PINNs. Exploiting elementary properties of fundamental solutions of linear differential operators, we present a principled and simple way to handle point sources in inverse problems. We demonstrate the excellent performance of PIBI-Nets for the Laplace and Poisson equations, both on artificial data sets and within a real-world application concerning the reconstruction of groundwater flows.
Conditional Matrix Flows for Gaussian Graphical Models
Jun 12, 2023Abstract:Studying conditional independence structure among many variables with few observations is a challenging task. Gaussian Graphical Models (GGMs) tackle this problem by encouraging sparsity in the precision matrix through an $l_p$ regularization with $p\leq1$. However, since the objective is highly non-convex for sub-$l_1$ pseudo-norms, most approaches rely on the $l_1$ norm. In this case frequentist approaches allow to elegantly compute the solution path as a function of the shrinkage parameter $\lambda$. Instead of optimizing the penalized likelihood, the Bayesian formulation introduces a Laplace prior on the precision matrix. However, posterior inference for different $\lambda$ values requires repeated runs of expensive Gibbs samplers. We propose a very general framework for variational inference in GGMs that unifies the benefits of frequentist and Bayesian frameworks. Specifically, we propose to approximate the posterior with a matrix-variate Normalizing Flow defined on the space of symmetric positive definite matrices. As a key improvement on previous work, we train a continuum of sparse regression models jointly for all regularization parameters $\lambda$ and all $l_p$ norms, including non-convex sub-$l_1$ pseudo-norms. This is achieved by conditioning the flow on $p>0$ and on the shrinkage parameter $\lambda$. We have then access with one model to (i) the evolution of the posterior for any $\lambda$ and for any $l_p$ (pseudo-) norms, (ii) the marginal log-likelihood for model selection, and (iii) we can recover the frequentist solution paths as the MAP, which is obtained through simulated annealing.
Lagrangian Flow Networks for Conservation Laws
May 26, 2023



Abstract:We introduce Lagrangian Flow Networks (LFlows) for modeling fluid densities and velocities continuously in space and time. The proposed LFlows satisfy by construction the continuity equation, a PDE describing mass conservation in its differentiable form. Our model is based on the insight that solutions to the continuity equation can be expressed as time-dependent density transformations via differentiable and invertible maps. This follows from classical theory of existence and uniqueness of Lagrangian flows for smooth vector fields. Hence, we model fluid densities by transforming a base density with parameterized diffeomorphisms conditioned on time. The key benefit compared to methods relying on Neural-ODE or PINNs is that the analytic expression of the velocity is always consistent with the density. Furthermore, there is no need for expensive numerical solvers, nor for enforcing the PDE with penalty methods. Lagrangian Flow Networks show improved predictive accuracy on synthetic density modeling tasks compared to competing models in both 2D and 3D. We conclude with a real-world application of modeling bird migration based on sparse weather radar measurements.
Truly Mesh-free Physics-Informed Neural Networks
Jun 03, 2022

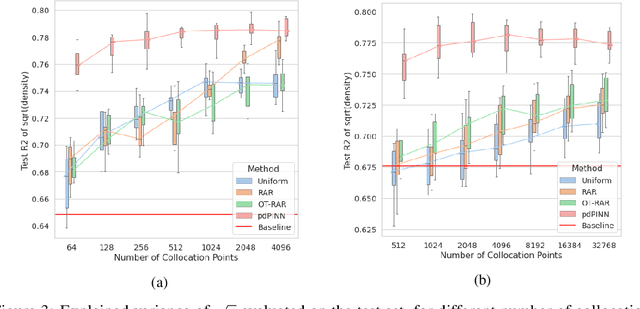
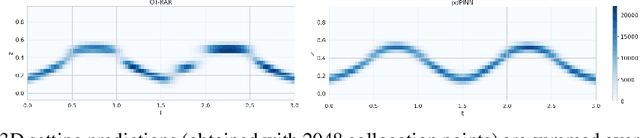
Abstract:Physics-informed Neural Networks (PINNs) have recently emerged as a principled way to include prior physical knowledge in form of partial differential equations (PDEs) into neural networks. Although generally viewed as being mesh-free, current approaches still rely on collocation points obtained within a bounded region, even in settings with spatially sparse signals. Furthermore, if the boundaries are not known, the selection of such a region may be arbitrary, resulting in a large proportion of collocation points being selected in areas of low relevance. To resolve this, we present a mesh-free and adaptive approach termed particle-density PINN (pdPINN), which is inspired by the microscopic viewpoint of fluid dynamics. Instead of sampling from a bounded region, we propose to sample directly from the distribution over the (fluids) particle positions, eliminating the need to introduce boundaries while adaptively focusing on the most relevant regions. This is achieved by reformulating the modeled fluid density as an unnormalized probability distribution from which we sample with dynamic Monte Carlo methods. We further generalize pdPINNs to different settings that allow interpreting a positive scalar quantity as a particle density, such as the evolution of the temperature in the heat equation. The utility of our approach is demonstrated on experiments for modeling (non-steady) compressible fluids in up to three dimensions and a two-dimensional diffusion problem, illustrating the high flexibility and sample efficiency compared to existing refinement methods for PINNs.
Learning Invariances with Generalised Input-Convex Neural Networks
Apr 14, 2022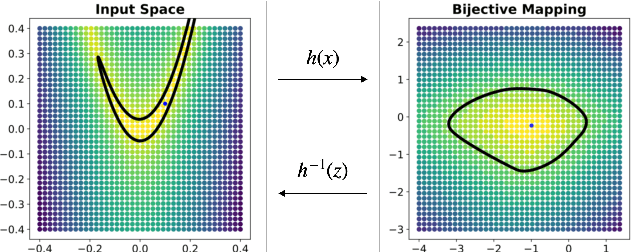
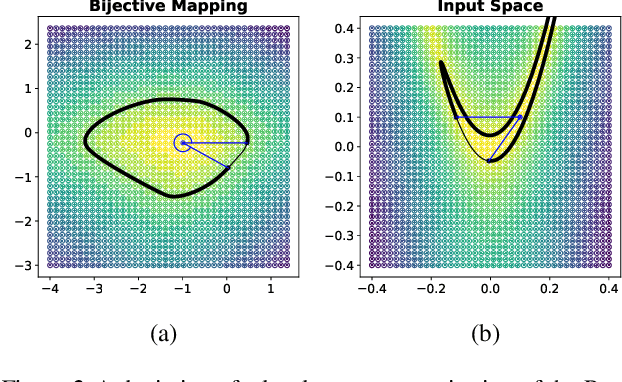
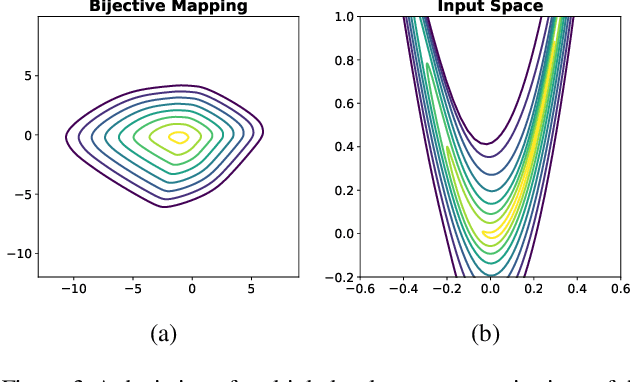
Abstract:Considering smooth mappings from input vectors to continuous targets, our goal is to characterise subspaces of the input domain, which are invariant under such mappings. Thus, we want to characterise manifolds implicitly defined by level sets. Specifically, this characterisation should be of a global parametric form, which is especially useful for different informed data exploration tasks, such as building grid-based approximations, sampling points along the level curves, or finding trajectories on the manifold. However, global parameterisations can only exist if the level sets are connected. For this purpose, we introduce a novel and flexible class of neural networks that generalise input-convex networks. These networks represent functions that are guaranteed to have connected level sets forming smooth manifolds on the input space. We further show that global parameterisations of these level sets can be always found efficiently. Lastly, we demonstrate that our novel technique for characterising invariances is a powerful generative data exploration tool in real-world applications, such as computational chemistry.
Learning Conditional Invariance through Cycle Consistency
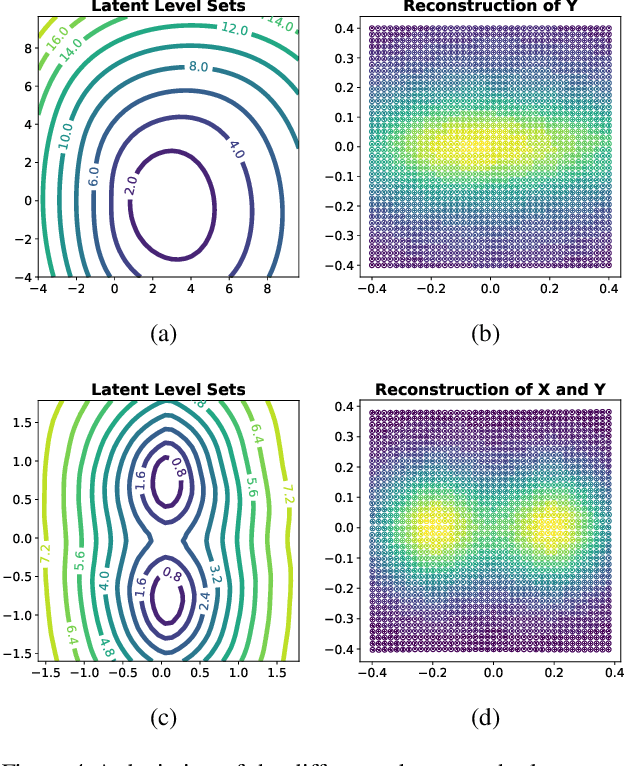
Nov 25, 2021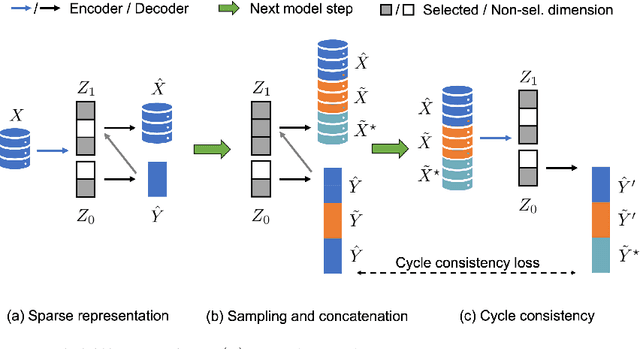
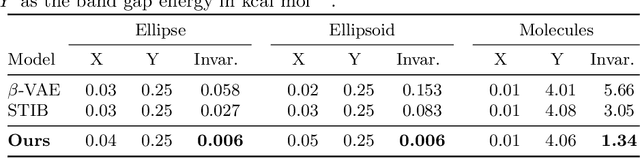
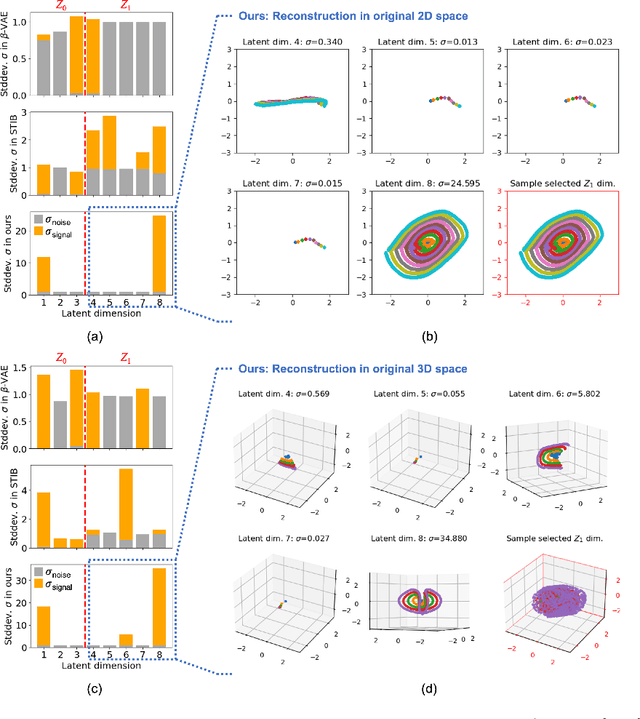
Abstract:Identifying meaningful and independent factors of variation in a dataset is a challenging learning task frequently addressed by means of deep latent variable models. This task can be viewed as learning symmetry transformations preserving the value of a chosen property along latent dimensions. However, existing approaches exhibit severe drawbacks in enforcing the invariance property in the latent space. We address these shortcomings with a novel approach to cycle consistency. Our method involves two separate latent subspaces for the target property and the remaining input information, respectively. In order to enforce invariance as well as sparsity in the latent space, we incorporate semantic knowledge by using cycle consistency constraints relying on property side information. The proposed method is based on the deep information bottleneck and, in contrast to other approaches, allows using continuous target properties and provides inherent model selection capabilities. We demonstrate on synthetic and molecular data that our approach identifies more meaningful factors which lead to sparser and more interpretable models with improved invariance properties.
3DMolNet: A Generative Network for Molecular Structures
Oct 08, 2020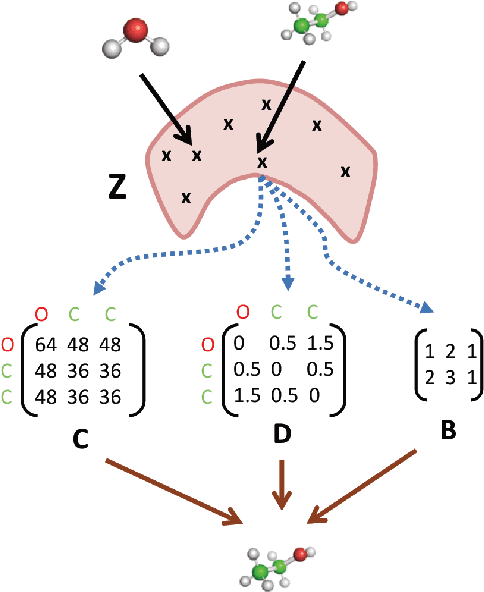
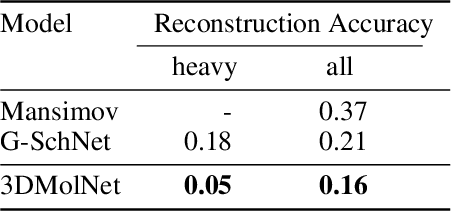
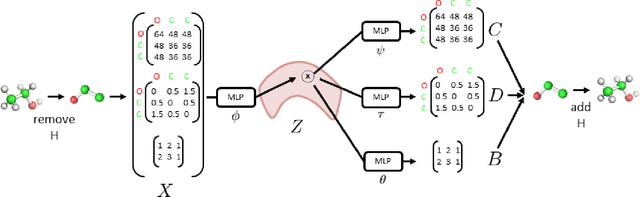
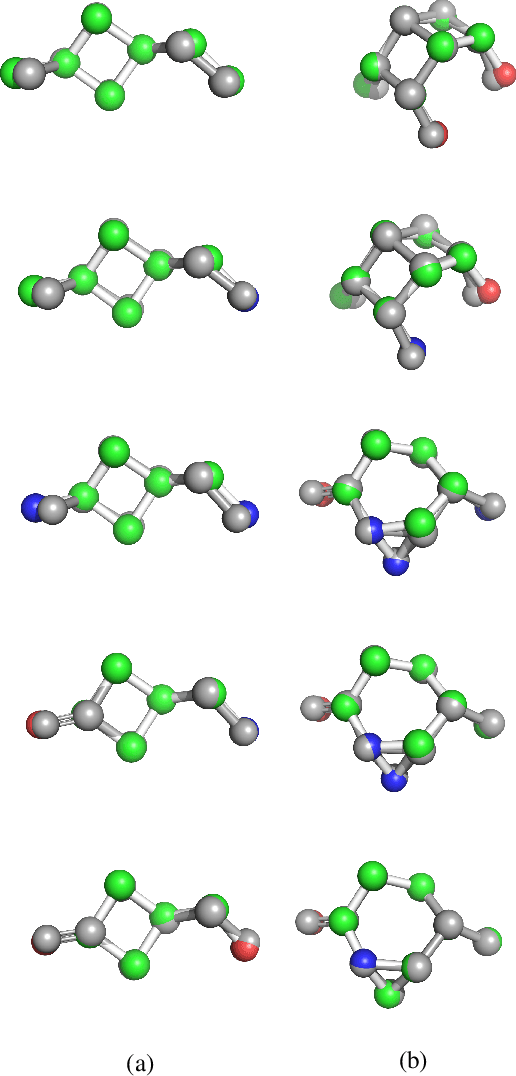
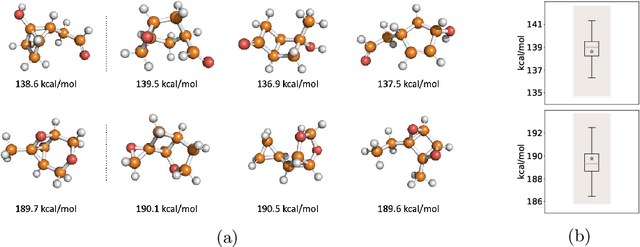
Abstract:With the recent advances in machine learning for quantum chemistry, it is now possible to predict the chemical properties of compounds and to generate novel molecules. Existing generative models mostly use a string- or graph-based representation, but the precise three-dimensional coordinates of the atoms are usually not encoded. First attempts in this direction have been proposed, where autoregressive or GAN-based models generate atom coordinates. Those either lack a latent space in the autoregressive setting, such that a smooth exploration of the compound space is not possible, or cannot generalize to varying chemical compositions. We propose a new approach to efficiently generate molecular structures that are not restricted to a fixed size or composition. Our model is based on the variational autoencoder which learns a translation-, rotation-, and permutation-invariant low-dimensional representation of molecules. Our experiments yield a mean reconstruction error below 0.05 Angstrom, outperforming the current state-of-the-art methods by a factor of four, and which is even lower than the spatial quantization error of most chemical descriptors. The compositional and structural validity of newly generated molecules has been confirmed by quantum chemical methods in a set of experiments.
On the Empirical Neural Tangent Kernel of Standard Finite-Width Convolutional Neural Network Architectures
Jun 24, 2020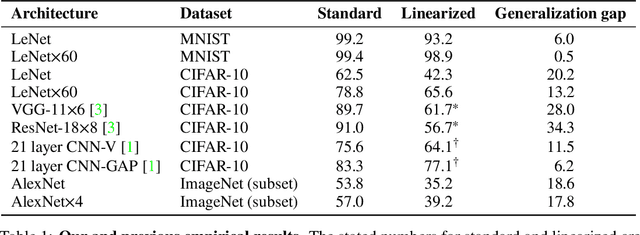
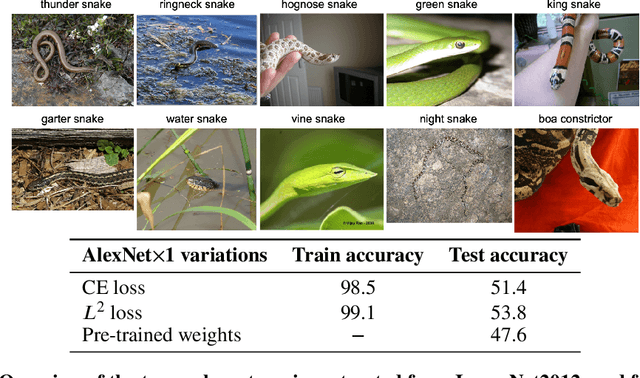
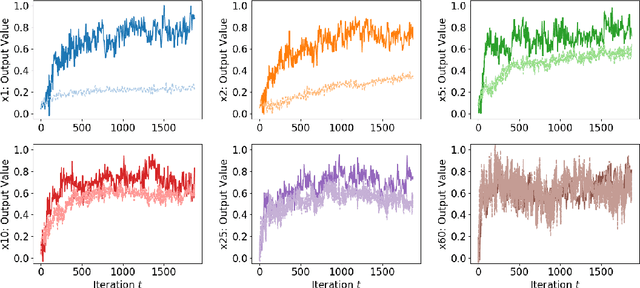
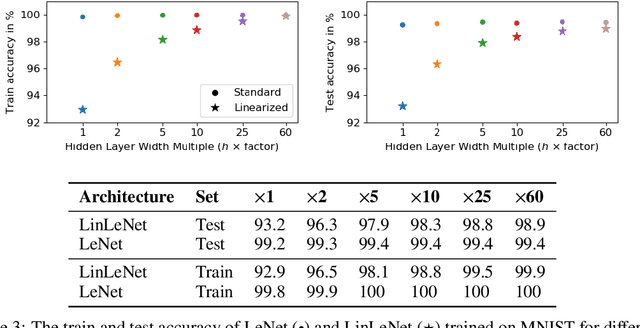
Abstract:The Neural Tangent Kernel (NTK) is an important milestone in the ongoing effort to build a theory for deep learning. Its prediction that sufficiently wide neural networks behave as kernel methods, or equivalently as random feature models, has been confirmed empirically for certain wide architectures. It remains an open question how well NTK theory models standard neural network architectures of widths common in practice, trained on complex datasets such as ImageNet. We study this question empirically for two well-known convolutional neural network architectures, namely AlexNet and LeNet, and find that their behavior deviates significantly from their finite-width NTK counterparts. For wider versions of these networks, where the number of channels and widths of fully-connected layers are increased, the deviation decreases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge