Learning Conditional Invariance through Cycle Consistency

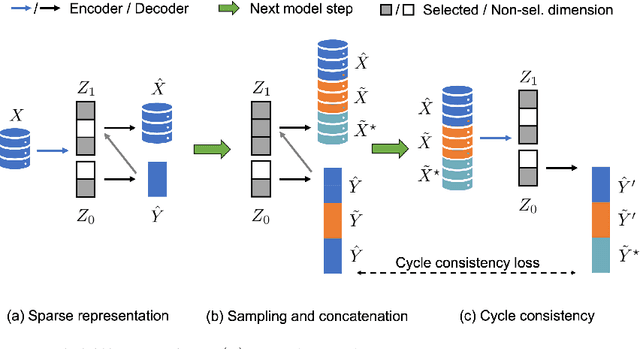
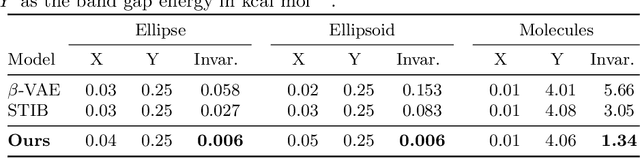
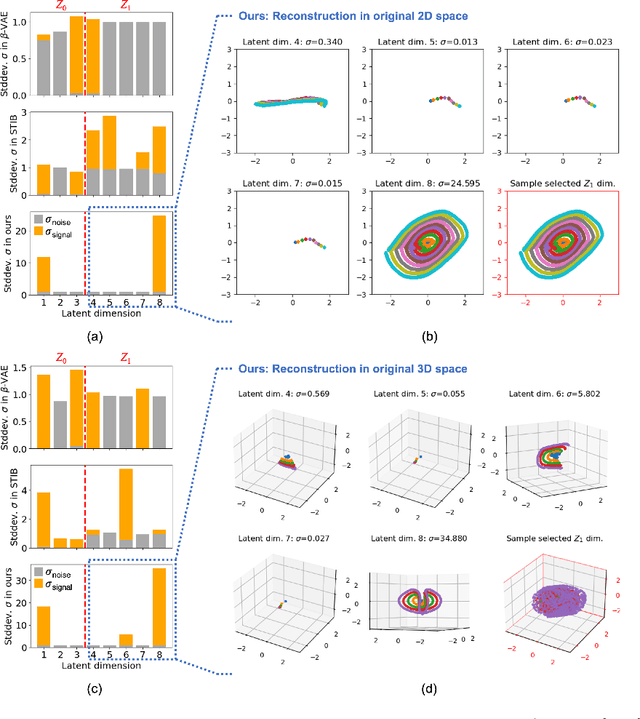
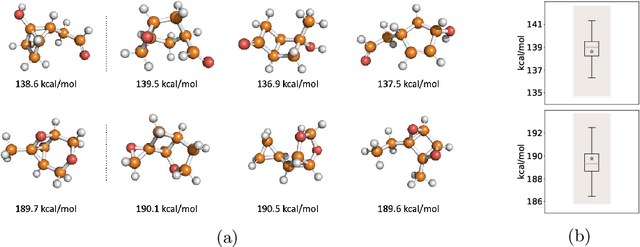
Identifying meaningful and independent factors of variation in a dataset is a challenging learning task frequently addressed by means of deep latent variable models. This task can be viewed as learning symmetry transformations preserving the value of a chosen property along latent dimensions. However, existing approaches exhibit severe drawbacks in enforcing the invariance property in the latent space. We address these shortcomings with a novel approach to cycle consistency. Our method involves two separate latent subspaces for the target property and the remaining input information, respectively. In order to enforce invariance as well as sparsity in the latent space, we incorporate semantic knowledge by using cycle consistency constraints relying on property side information. The proposed method is based on the deep information bottleneck and, in contrast to other approaches, allows using continuous target properties and provides inherent model selection capabilities. We demonstrate on synthetic and molecular data that our approach identifies more meaningful factors which lead to sparser and more interpretable models with improved invariance properties.

Inverse Learning of Symmetry Transformations

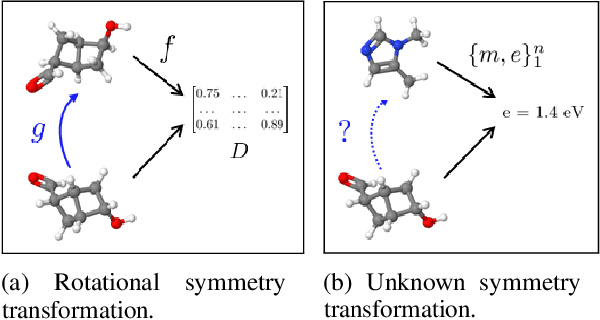
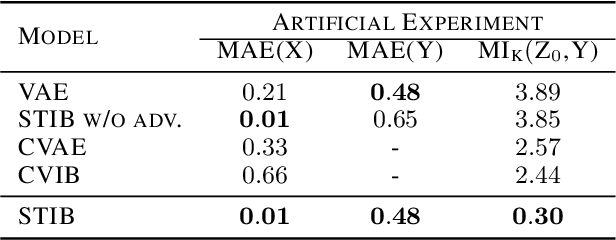
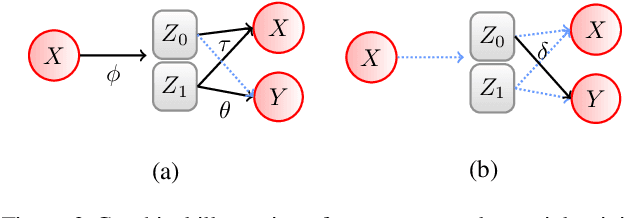
Symmetry transformations induce invariances and are a crucial building block of modern machine learning algorithms. Some transformations can be described analytically, e.g. geometric invariances. However, in many complex domains, such as the chemical space, invariances can be observed yet the corresponding symmetry transformation cannot be formulated analytically. Thus, the goal of our work is to learn the symmetry transformation that induced this invariance. To address this task, we propose learning two latent subspaces, where the first subspace captures the property and the second subspace the remaining invariant information. Our approach is based on the deep information bottleneck principle in combination with a mutual information regulariser. Unlike previous methods however, we focus on estimating mutual information in continuous rather than binary settings. This poses many challenges as mutual information cannot be meaningfully minimised in continuous domains. Therefore, we base the calculation of mutual information on correlation matrices in combination with a bijective variable transformation. Extensive experiments demonstrate that our model outperforms state-of-the-art methods on artificial and molecular datasets.

On the Difference Between the Information Bottleneck and the Deep Information Bottleneck

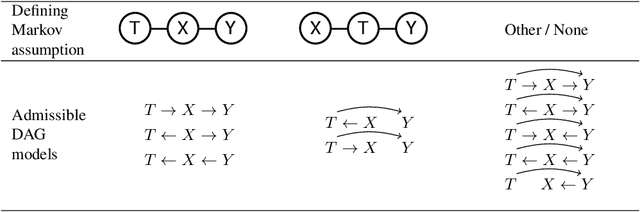
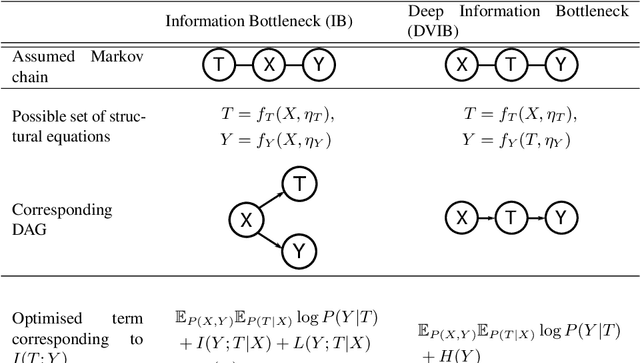
Combining the Information Bottleneck model with deep learning by replacing mutual information terms with deep neural nets has proved successful in areas ranging from generative modelling to interpreting deep neural networks. In this paper, we revisit the Deep Variational Information Bottleneck and the assumptions needed for its derivation. The two assumed properties of the data $X$, $Y$ and their latent representation $T$ take the form of two Markov chains $T-X-Y$ and $X-T-Y$. Requiring both to hold during the optimisation process can be limiting for the set of potential joint distributions $P(X,Y,T)$. We therefore show how to circumvent this limitation by optimising a lower bound for $I(T;Y)$ for which only the latter Markov chain has to be satisfied. The actual mutual information consists of the lower bound which is optimised in DVIB and cognate models in practice and of two terms measuring how much the former requirement $T-X-Y$ is violated. Finally, we propose to interpret the family of information bottleneck models as directed graphical models and show that in this framework the original and deep information bottlenecks are special cases of a fundamental IB model.

Informed MCMC with Bayesian Neural Networks for Facial Image Analysis

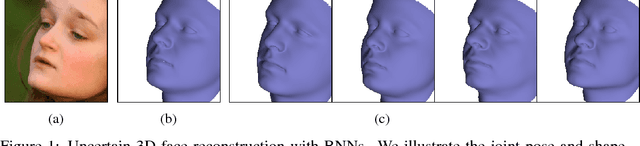
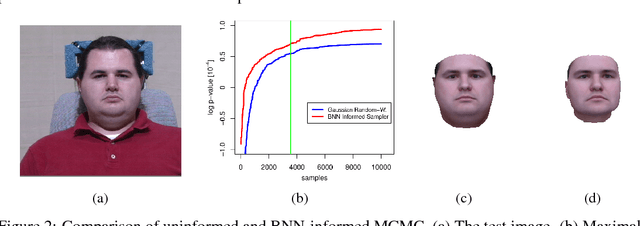
Computer vision tasks are difficult because of the large variability in the data that is induced by changes in light, background, partial occlusion as well as the varying pose, texture, and shape of objects. Generative approaches to computer vision allow us to overcome this difficulty by explicitly modeling the physical image formation process. Using generative object models, the analysis of an observed image is performed via Bayesian inference of the posterior distribution. This conceptually simple approach tends to fail in practice because of several difficulties stemming from sampling the posterior distribution: high-dimensionality and multi-modality of the posterior distribution as well as expensive simulation of the rendering process. The main difficulty of sampling approaches in a computer vision context is choosing the proposal distribution accurately so that maxima of the posterior are explored early and the algorithm quickly converges to a valid image interpretation. In this work, we propose to use a Bayesian Neural Network for estimating an image dependent proposal distribution. Compared to a standard Gaussian random walk proposal, this accelerates the sampler in finding regions of the posterior with high value. In this way, we can significantly reduce the number of samples needed to perform facial image analysis.

Learning Sparse Latent Representations with the Deep Copula Information Bottleneck

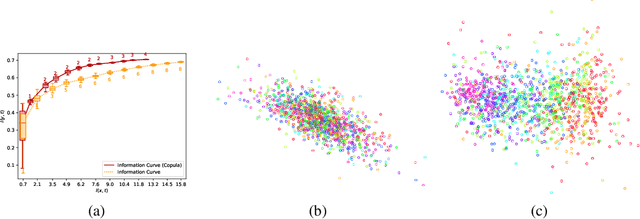
Deep latent variable models are powerful tools for representation learning. In this paper, we adopt the deep information bottleneck model, identify its shortcomings and propose a model that circumvents them. To this end, we apply a copula transformation which, by restoring the invariance properties of the information bottleneck method, leads to disentanglement of the features in the latent space. Building on that, we show how this transformation translates to sparsity of the latent space in the new model. We evaluate our method on artificial and real data.

Causal Compression

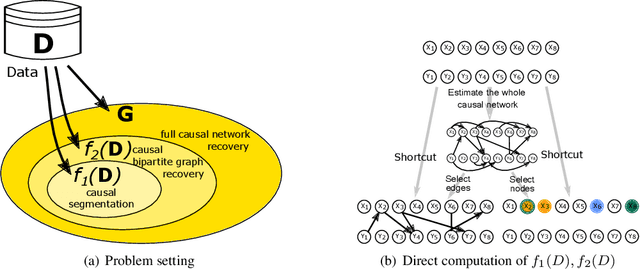
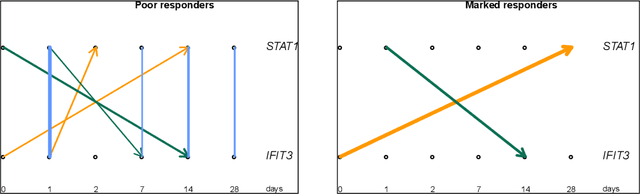
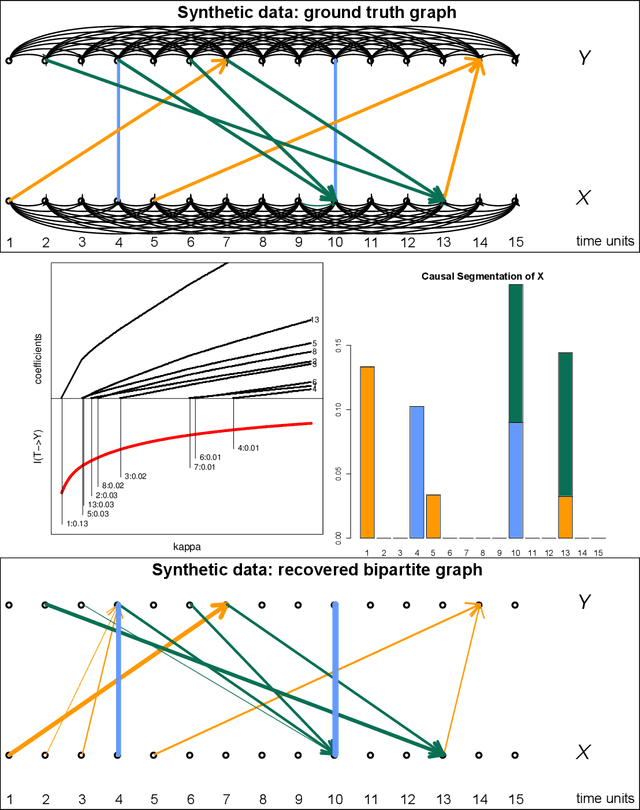
We propose a new method of discovering causal relationships in temporal data based on the notion of causal compression. To this end, we adopt the Pearlian graph setting and the directed information as an information theoretic tool for quantifying causality. We introduce chain rule for directed information and use it to motivate causal sparsity. We show two applications of the proposed method: causal time series segmentation which selects time points capturing the incoming and outgoing causal flow between time points belonging to different signals, and causal bipartite graph recovery. We prove that modelling of causality in the adopted set-up only requires estimating the copula density of the data distribution and thus does not depend on its marginals. We evaluate the method on time resolved gene expression data.

Bayesian Markov Blanket Estimation

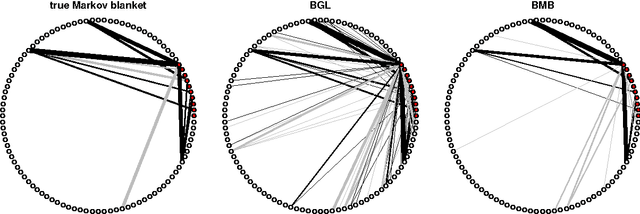
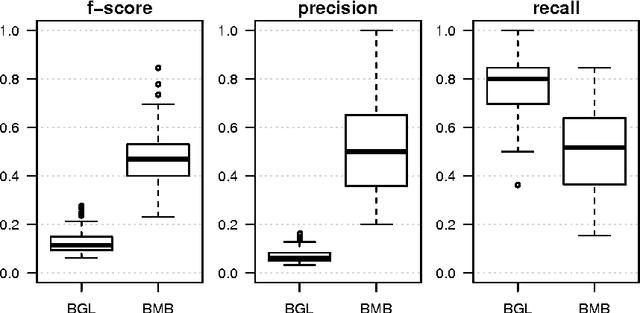
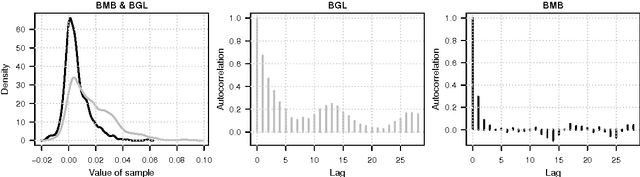
This paper considers a Bayesian view for estimating a sub-network in a Markov random field. The sub-network corresponds to the Markov blanket of a set of query variables, where the set of potential neighbours here is big. We factorize the posterior such that the Markov blanket is conditionally independent of the network of the potential neighbours. By exploiting this blockwise decoupling, we derive analytic expressions for posterior conditionals. Subsequently, we develop an inference scheme which makes use of the factorization. As a result, estimation of a sub-network is possible without inferring an entire network. Since the resulting Gibbs sampler scales linearly with the number of variables, it can handle relatively large neighbourhoods. The proposed scheme results in faster convergence and superior mixing of the Markov chain than existing Bayesian network estimation techniques.