Cognitive Non-Coherent Jamming Techniques for Frequency Selective Attacks

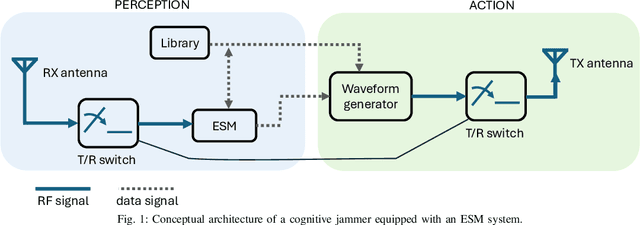
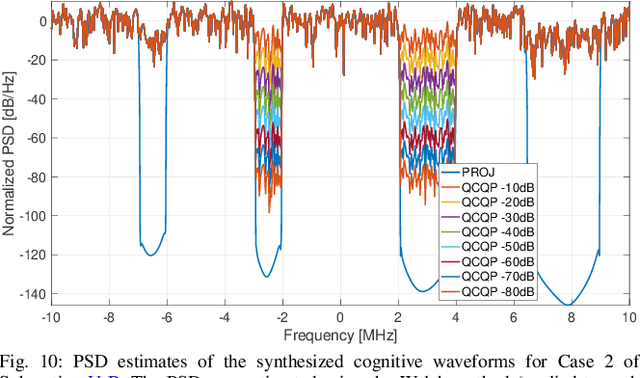
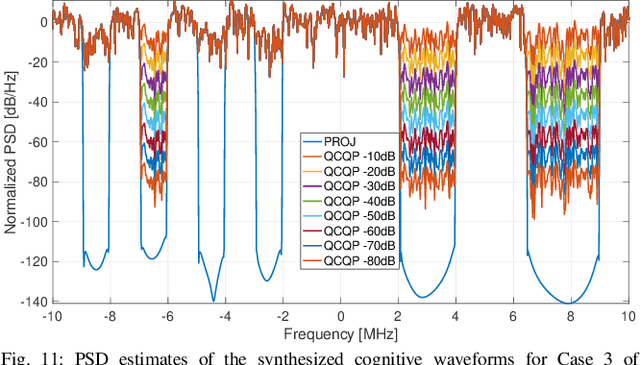
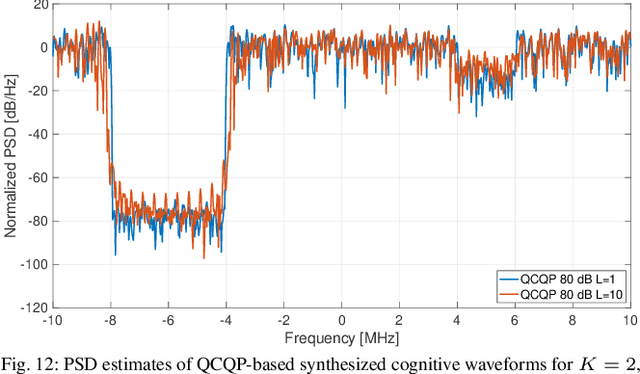
This paper deals with the design of non-coherent jamming strategies capable of ensuring spectral compatibility with friendly radio frequency (RF) emitters. The goal is achieved via a cognitive approach, which, after recognizing the presence of friendly RF systems within the bandwidth of interest (perception), synthesizes a jamming waveform (action) with spectral notches, that allows to interfere exclusively with opposite emissions. Two methods are proposed for the synthesis of the jamming signal. The former leverages optimization techniques for quadratically constrained quadratic problems (QCQP) where each constraint embeds the interference level tolerable by a specific friendly RF system. The latter is a very computationally efficient approach based on simple projections, allowing a control over the spectral notch positions and widths. At the analysis stage, the performance of the devised jamming techniques is firstly numerically analyzed in terms of spectral occupancy and autocorrelation characteristics. The impact of the quantization process involved in the digital-to-analog conversion (DAC) of the jamming waveforms is also examined, with a particular focus on the spectral shaping impairments resulting from reduced DAC resolution. Finally, waveform transmission and reception is experimentally assessed with software defined radio (SDR) devices.

Radar Code Design for the Joint Optimization of Detection Performance and Measurement Accuracy in Track Maintenance

This paper deals with the design of slow-time coded waveforms which jointly optimize the detection probability and the measurements accuracy for track maintenance in the presence of colored Gaussian interference. The output signal-to-interference-plus-noise ratio (SINR) and Cram\'er Rao bounds (CRBs) on time delay and Doppler shift are used as figures of merit to accomplish reliable detection as well as accurate measurements. The transmitted code is subject to radar power budget requirements and a similarity constraint. To tackle the resulting non-convex multi-objective optimization problem, a polynomial-time algorithm that integrates scalarization and tensor-based relaxation methods is developed. The corresponding relaxed multi-linear problems are solved by means of the maximum block improvement (MBI) framework, where the optimal solution at each iteration is obtained in closed form. Numeral results demonstrate the trade-off between the detection and the estimation performance, along with the acceptable Doppler robustness achieved by the proposed algorithm.