Victor Dorobantu
Conformal Generative Modeling on Triangulated Surfaces
Mar 17, 2023Abstract:We propose conformal generative modeling, a framework for generative modeling on 2D surfaces approximated by discrete triangle meshes. Our approach leverages advances in discrete conformal geometry to develop a map from a source triangle mesh to a target triangle mesh of a simple manifold such as a sphere. After accounting for errors due to the mesh discretization, we can use any generative modeling approach developed for simple manifolds as a plug-and-play subroutine. We demonstrate our framework on multiple complicated manifolds and multiple generative modeling subroutines, where we show that our approach can learn good estimates of distributions on meshes from samples, and can also learn simultaneously from multiple distinct meshes of the same underlying manifold.
DizzyRNN: Reparameterizing Recurrent Neural Networks for Norm-Preserving Backpropagation
Dec 13, 2016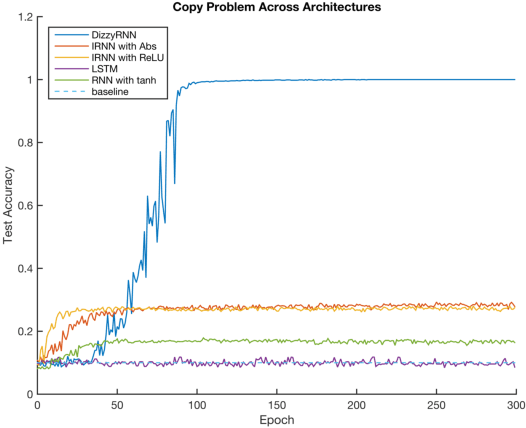
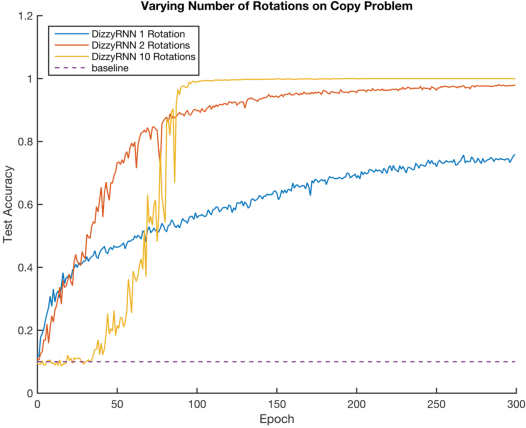
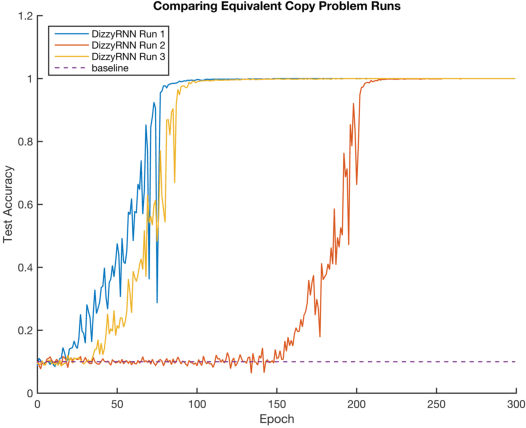
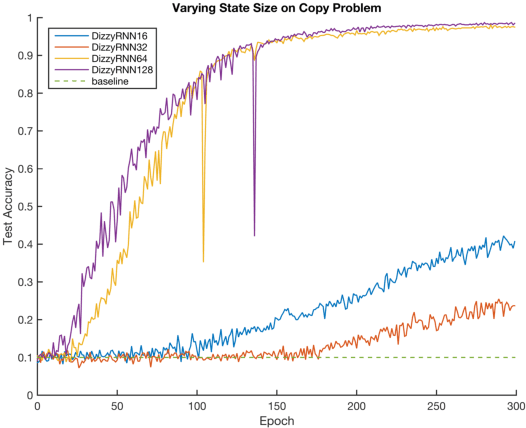
Abstract:The vanishing and exploding gradient problems are well-studied obstacles that make it difficult for recurrent neural networks to learn long-term time dependencies. We propose a reparameterization of standard recurrent neural networks to update linear transformations in a provably norm-preserving way through Givens rotations. Additionally, we use the absolute value function as an element-wise non-linearity to preserve the norm of backpropagated signals over the entire network. We show that this reparameterization reduces the number of parameters and maintains the same algorithmic complexity as a standard recurrent neural network, while outperforming standard recurrent neural networks with orthogonal initializations and Long Short-Term Memory networks on the copy problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge