Improving Controller Generalization with Dimensionless Markov Decision Processes

Controllers trained with Reinforcement Learning tend to be very specialized and thus generalize poorly when their testing environment differs from their training one. We propose a Model-Based approach to increase generalization where both world model and policy are trained in a dimensionless state-action space. To do so, we introduce the Dimensionless Markov Decision Process ($\Pi$-MDP): an extension of Contextual-MDPs in which state and action spaces are non-dimensionalized with the Buckingham-$\Pi$ theorem. This procedure induces policies that are equivariant with respect to changes in the context of the underlying dynamics. We provide a generic framework for this approach and apply it to a model-based policy search algorithm using Gaussian Process models. We demonstrate the applicability of our method on simulated actuated pendulum and cartpole systems, where policies trained on a single environment are robust to shifts in the distribution of the context.

Learning Robust Controllers Via Probabilistic Model-Based Policy Search

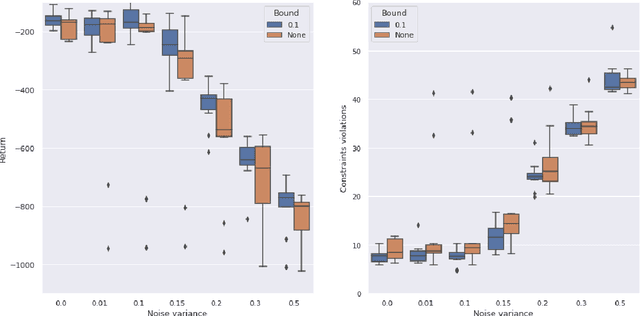
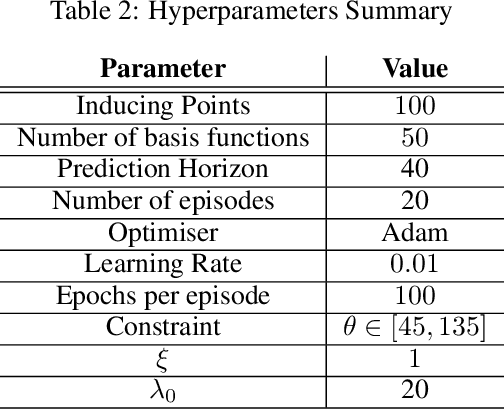
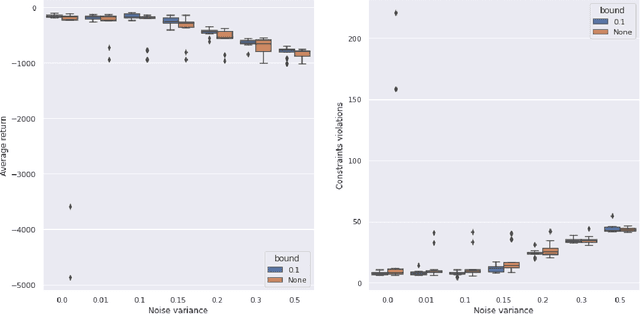
Model-based Reinforcement Learning estimates the true environment through a world model in order to approximate the optimal policy. This family of algorithms usually benefits from better sample efficiency than their model-free counterparts. We investigate whether controllers learned in such a way are robust and able to generalize under small perturbations of the environment. Our work is inspired by the PILCO algorithm, a method for probabilistic policy search. We show that enforcing a lower bound to the likelihood noise in the Gaussian Process dynamics model regularizes the policy updates and yields more robust controllers. We demonstrate the empirical benefits of our method in a simulation benchmark.

Probabilistic selection of inducing points in sparse Gaussian processes

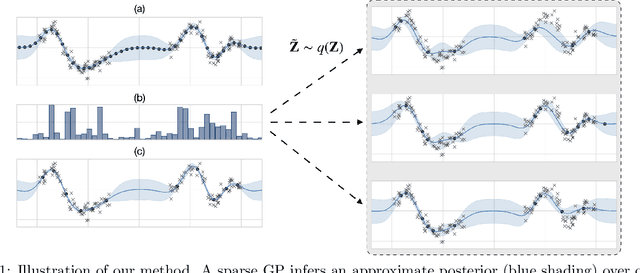
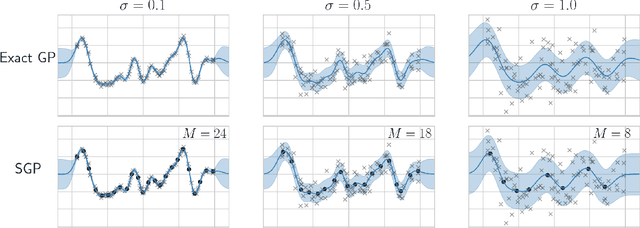
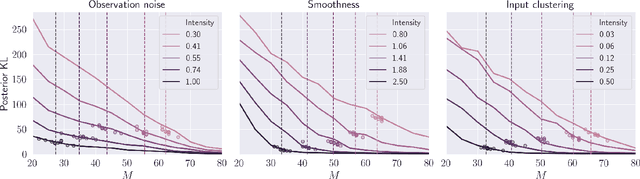
Sparse Gaussian processes and various extensions thereof are enabled through inducing points, that simultaneously bottleneck the predictive capacity and act as the main contributor towards model complexity. However, the number of inducing points is generally not associated with uncertainty which prevents us from applying the apparatus of Bayesian reasoning in identifying an appropriate trade-off. In this work we place a point process prior on the inducing points and approximate the associated posterior through stochastic variational inference. By letting the prior encourage a moderate number of inducing points, we enable the model to learn which and how many points to utilise. We experimentally show that fewer inducing points are preferred by the model as the points become less informative, and further demonstrate how the method can be applied in deep Gaussian processes and latent variable modelling.