Higher-Order Convolution Improves Neural Predictivity in the Retina

We present a novel approach to neural response prediction that incorporates higher-order operations directly within convolutional neural networks (CNNs). Our model extends traditional 3D CNNs by embedding higher-order operations within the convolutional operator itself, enabling direct modeling of multiplicative interactions between neighboring pixels across space and time. Our model increases the representational power of CNNs without increasing their depth, therefore addressing the architectural disparity between deep artificial networks and the relatively shallow processing hierarchy of biological visual systems. We evaluate our approach on two distinct datasets: salamander retinal ganglion cell (RGC) responses to natural scenes, and a new dataset of mouse RGC responses to controlled geometric transformations. Our higher-order CNN (HoCNN) achieves superior performance while requiring only half the training data compared to standard architectures, demonstrating correlation coefficients up to 0.75 with neural responses (against 0.80$\pm$0.02 retinal reliability). When integrated into state-of-the-art architectures, our approach consistently improves performance across different species and stimulus conditions. Analysis of the learned representations reveals that our network naturally encodes fundamental geometric transformations, particularly scaling parameters that characterize object expansion and contraction. This capability is especially relevant for specific cell types, such as transient OFF-alpha and transient ON cells, which are known to detect looming objects and object motion respectively, and where our model shows marked improvement in response prediction. The correlation coefficients for scaling parameters are more than twice as high in HoCNN (0.72) compared to baseline models (0.32).

Convolution goes higher-order: a biologically inspired mechanism empowers image classification

We propose a novel approach to image classification inspired by complex nonlinear biological visual processing, whereby classical convolutional neural networks (CNNs) are equipped with learnable higher-order convolutions. Our model incorporates a Volterra-like expansion of the convolution operator, capturing multiplicative interactions akin to those observed in early and advanced stages of biological visual processing. We evaluated this approach on synthetic datasets by measuring sensitivity to testing higher-order correlations and performance in standard benchmarks (MNIST, FashionMNIST, CIFAR10, CIFAR100 and Imagenette). Our architecture outperforms traditional CNN baselines, and achieves optimal performance with expansions up to 3rd/4th order, aligning remarkably well with the distribution of pixel intensities in natural images. Through systematic perturbation analysis, we validate this alignment by isolating the contributions of specific image statistics to model performance, demonstrating how different orders of convolution process distinct aspects of visual information. Furthermore, Representational Similarity Analysis reveals distinct geometries across network layers, indicating qualitatively different modes of visual information processing. Our work bridges neuroscience and deep learning, offering a path towards more effective, biologically inspired computer vision models. It provides insights into visual information processing and lays the groundwork for neural networks that better capture complex visual patterns, particularly in resource-constrained scenarios.

A new inference approach for training shallow and deep generalized linear models of noisy interacting neurons

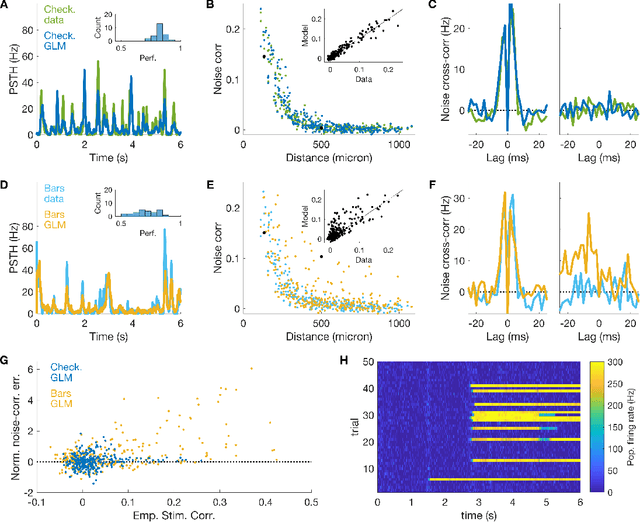
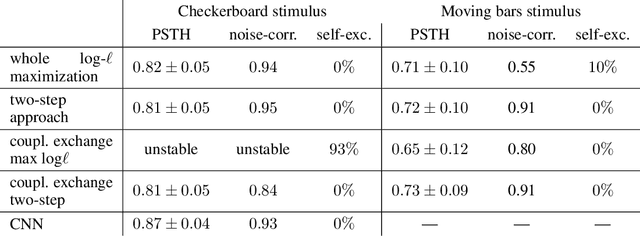
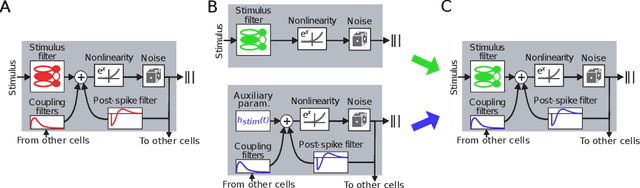
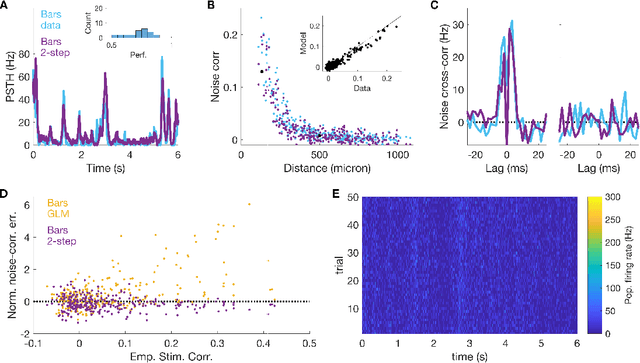
Generalized linear models are one of the most efficient paradigms for predicting the correlated stochastic activity of neuronal networks in response to external stimuli, with applications in many brain areas. However, when dealing with complex stimuli, their parameters often do not generalize across different stimulus statistics, leading to degraded performance and blowup instabilities. Here, we develop a two-step inference strategy that allows us to train robust generalized linear models of interacting neurons, by explicitly separating the effects of stimulus correlations and noise correlations in each training step. Applying this approach to the responses of retinal ganglion cells to complex visual stimuli, we show that, compared to classical methods, the models trained in this way exhibit improved performance, are more stable, yield robust interaction networks, and generalize well across complex visual statistics. The method can be extended to deep convolutional neural networks, leading to models with high predictive accuracy for both the neuron firing rates and their correlations.