Minimum Time Strategies for a Differential Drive Robot Escaping from a Circular Detection Region

A Differential Drive Robot (DDR) located inside a circular detection region in the plane wants to escape from it in minimum time. Various robotics applications can be modeled like the previous problem, such as a DDR escaping as soon as possible from a forbidden/dangerous region in the plane or running out from the sensor footprint of an unmanned vehicle flying at a constant altitude. In this paper, we find the motion strategies to accomplish its goal under two scenarios. In one, the detection region moves slower than the DDR and seeks to prevent escape; in another, its position is fixed. We formulate the problem as a zero-sum pursuit-evasion game, and using differential games theory, we compute the players' time-optimal motion strategies. Given the DDR's speed advantage, it can always escape by translating away from the center of the detection region at maximum speed. In this work, we show that the previous strategy could be optimal in some cases; however, other motion strategies emerge based on the player's speed ratio and the players' initial configurations.

A Surveillance Game between a Differential Drive Robot and an Omnidirectional Agent: The Case of a Faster Evader

A fundamental task in mobile robotics is to keep an agent under surveillance using an autonomous robotic platform equipped with a sensing device. Using differential game theory, we study a particular setup of the previous problem. A Differential Drive Robot (DDR) equipped with a bounded range sensor wants to keep surveillance of an Omnidirectional Agent (OA). The goal of the DDR is to maintain the OA inside its detection region for as much time as possible, while the OA, having the opposite goal, wants to leave the regions as soon as possible. We formulate the problem as a zero-sum differential game, and we compute the time-optimal motion strategies of the players to achieve their goals. We focus on the case where the OA is faster than the DDR. Given the OA's speed advantage, a winning strategy for the OA is always moving radially outwards to the DDR's position. However, this work shows that even though the previous strategy could be optimal in some cases, more complex motion strategies emerge based on the players' speed ratio. In particular, we exhibit that four classes of singular surfaces may appear in this game: Dispersal, Transition, Universal, and Focal surfaces. Each one of those surfaces implies a particular motion strategy for the players.

A Game Between Two Identical Dubins Cars: Evading a Conic Sensor in Minimum Time

A fundamental task in mobile robotics is keeping an intelligent agent under surveillance with an autonomous robot as it travels in the environment. This work studies a version of that problem involving one of the most popular vehicle platforms in robotics. In particular, we consider two identical Dubins cars moving on a plane without obstacles. One of them plays as the pursuer, and it is equipped with a limited field-of-view detection region modeled as a semi-infinite cone with its apex at the pursuer's position. The pursuer aims to maintain the other Dubins car, which plays as the evader, as much time as possible inside its detection region. On the contrary, the evader wants to escape as soon as possible. In this work, employing differential game theory, we find the time-optimal motion strategies near the game's end. The analysis of those trajectories reveals the existence of at least two singular surfaces: a Transition Surface and an Evader's Universal Surface. We also found that the barrier's standard construction produces a surface that partially lies outside the playing space and fails to define a closed region, implying that an additional procedure is required to determine all configurations where the evader escapes.

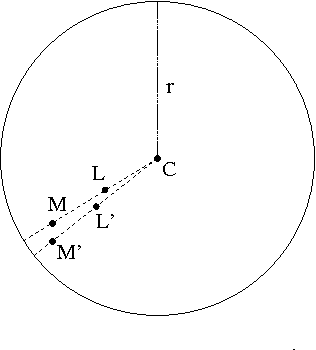
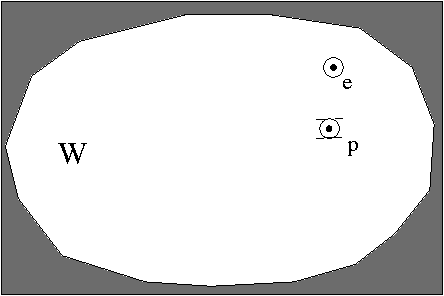
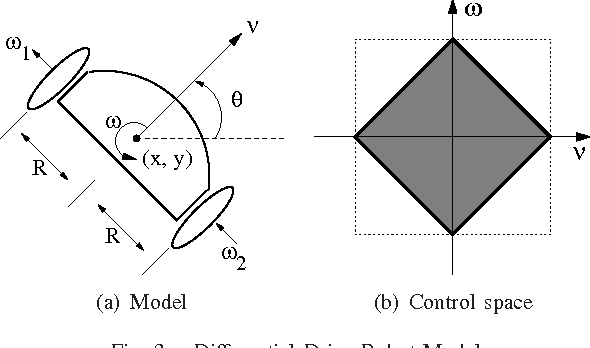
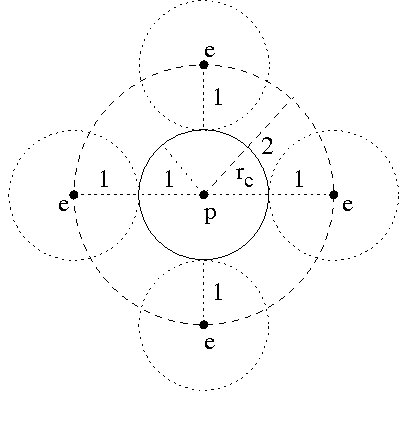
Capturing an Omnidirectional Evader in Convex Environments using a Differential Drive Robot

We study the problem of capturing an Omnidirectional Evader in convex environments using a Differential Drive Robot (DDR). The DDR wins the game if at any time instant it captures (collides with) the evader. The evader wins if it can avoid capture forever. Both players are unit disks with the same maximum (bounded) speed, but the DDR can only change its motion direction at a bounded rate. We show that despite this limitation, the DDR can capture the evader.