Neural DAEs: Constrained neural networks

In this article we investigate the effect of explicitly adding auxiliary trajectory information to neural networks for dynamical systems. We draw inspiration from the field of differential-algebraic equations and differential equations on manifolds and implement similar methods in residual neural networks. We discuss constraints through stabilization as well as projection methods, and show when to use which method based on experiments involving simulations of multi-body pendulums and molecular dynamics scenarios. Several of our methods are easy to implement in existing code and have limited impact on training performance while giving significant boosts in terms of inference.

A-Optimal Active Learning

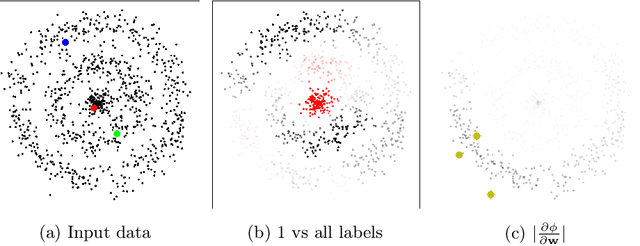
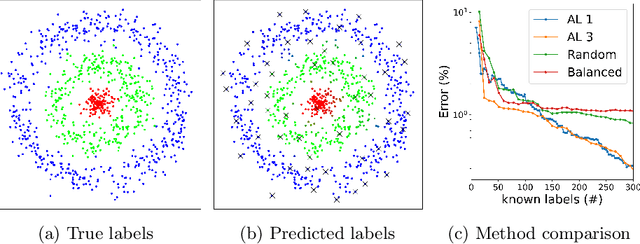
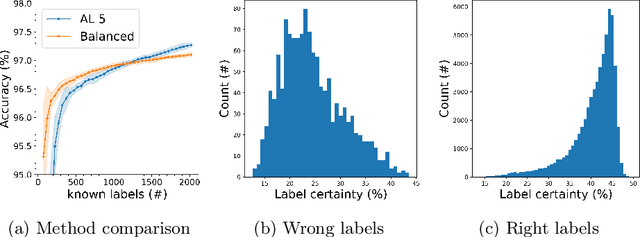
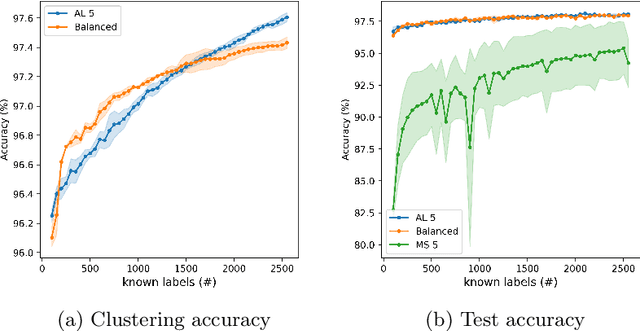
In this work we discuss the problem of active learning. We present an approach that is based on A-optimal experimental design of ill-posed problems and show how one can optimally label a data set by partially probing it, and use it to train a deep network. We present two approaches that make different assumptions on the data set. The first is based on a Bayesian interpretation of the semi-supervised learning problem with the graph Laplacian that is used for the prior distribution and the second is based on a frequentist approach, that updates the estimation of the bias term based on the recovery of the labels. We demonstrate that this approach can be highly efficient for estimating labels and training a deep network.

Mimetic Neural Networks: A unified framework for Protein Design and Folding

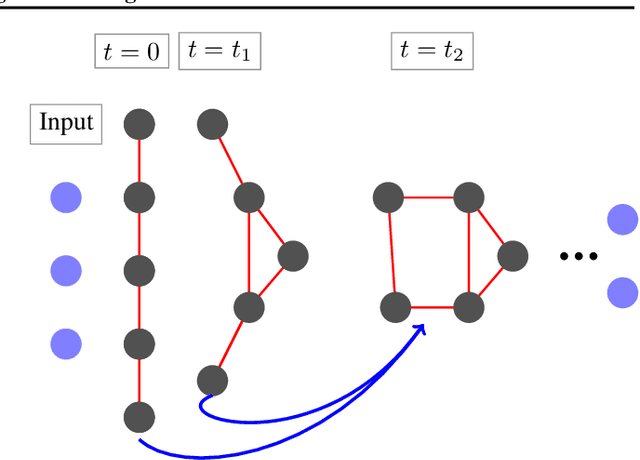
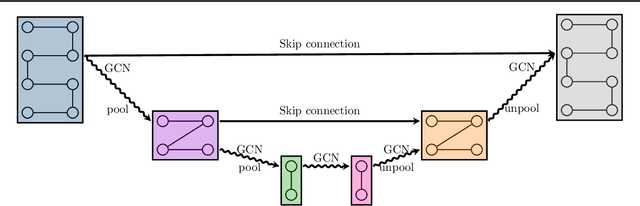
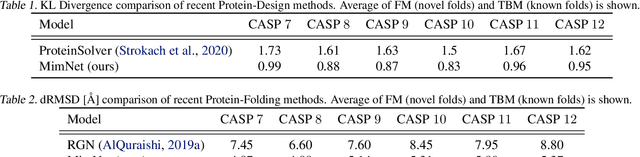
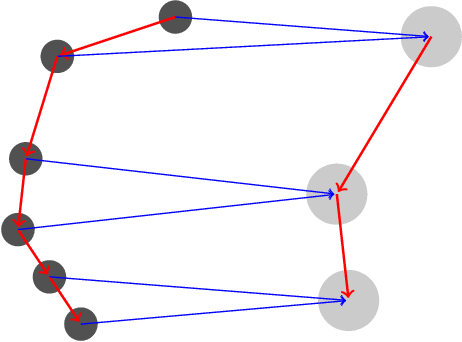
Recent advancements in machine learning techniques for protein folding motivate better results in its inverse problem -- protein design. In this work we introduce a new graph mimetic neural network, MimNet, and show that it is possible to build a reversible architecture that solves the structure and design problems in tandem, allowing to improve protein design when the structure is better estimated. We use the ProteinNet data set and show that the state of the art results in protein design can be improved, given recent architectures for protein folding.