Fast Parallel Randomized Algorithm for Nonnegative Matrix Factorization with KL Divergence for Large Sparse Datasets

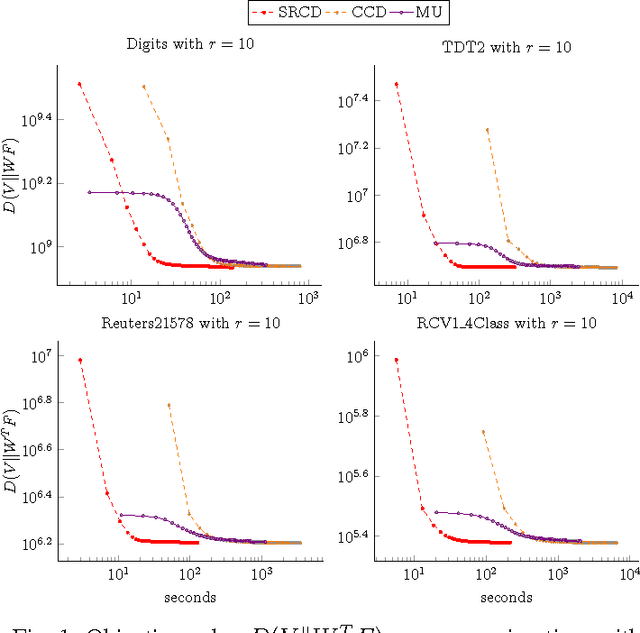
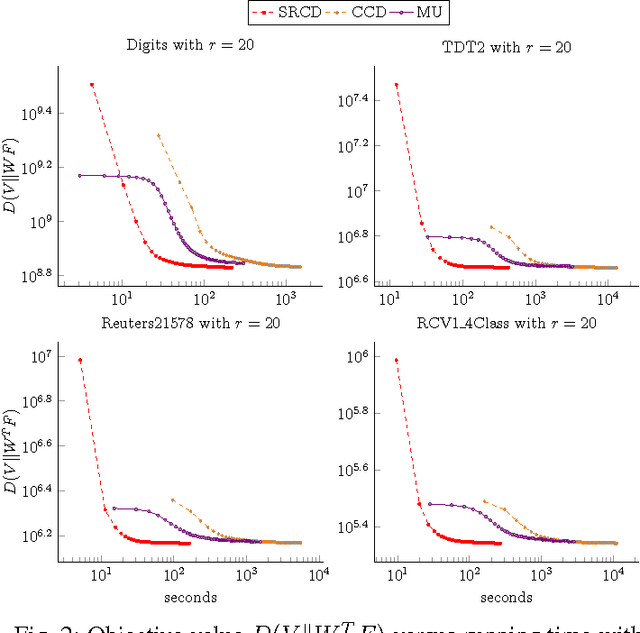
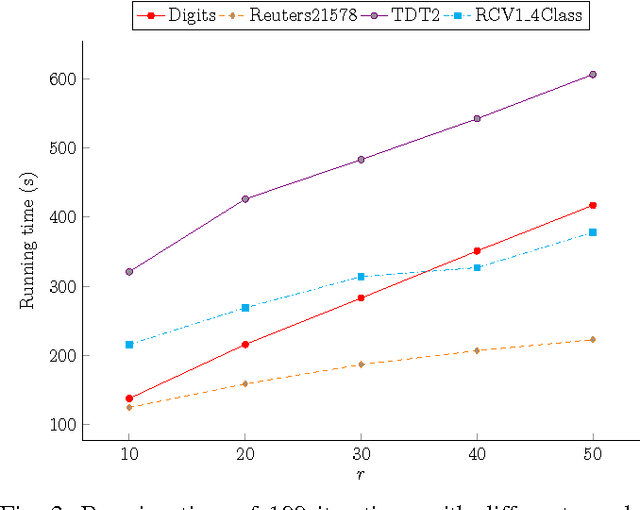
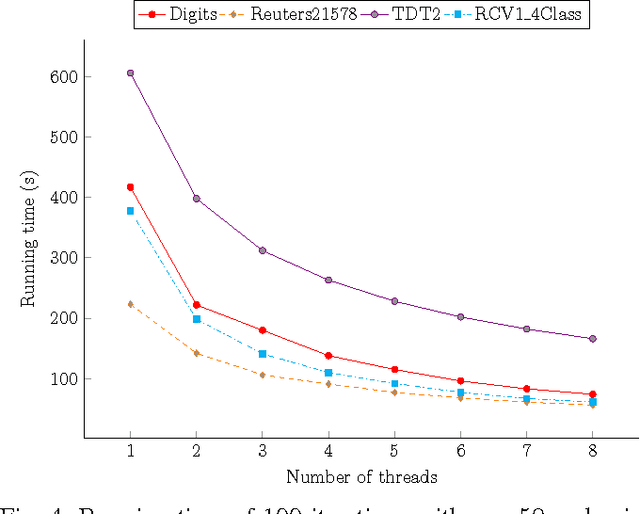
Nonnegative Matrix Factorization (NMF) with Kullback-Leibler Divergence (NMF-KL) is one of the most significant NMF problems and equivalent to Probabilistic Latent Semantic Indexing (PLSI), which has been successfully applied in many applications. For sparse count data, a Poisson distribution and KL divergence provide sparse models and sparse representation, which describe the random variation better than a normal distribution and Frobenius norm. Specially, sparse models provide more concise understanding of the appearance of attributes over latent components, while sparse representation provides concise interpretability of the contribution of latent components over instances. However, minimizing NMF with KL divergence is much more difficult than minimizing NMF with Frobenius norm; and sparse models, sparse representation and fast algorithms for large sparse datasets are still challenges for NMF with KL divergence. In this paper, we propose a fast parallel randomized coordinate descent algorithm having fast convergence for large sparse datasets to archive sparse models and sparse representation. The proposed algorithm's experimental results overperform the current studies' ones in this problem.

Inference in topic models: sparsity and trade-off

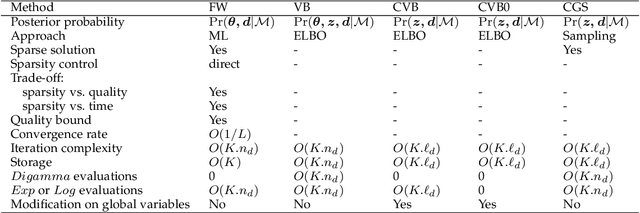
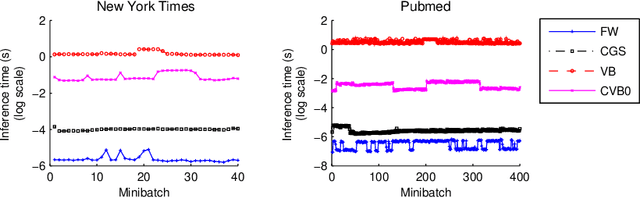
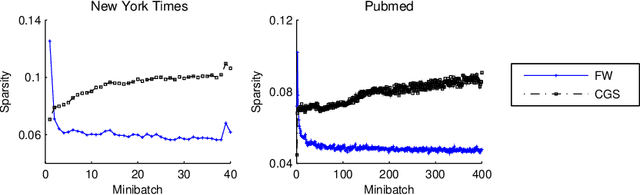
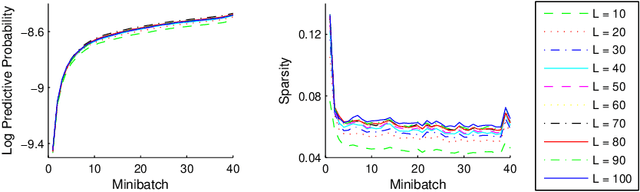
Topic models are popular for modeling discrete data (e.g., texts, images, videos, links), and provide an efficient way to discover hidden structures/semantics in massive data. One of the core problems in this field is the posterior inference for individual data instances. This problem is particularly important in streaming environments, but is often intractable. In this paper, we investigate the use of the Frank-Wolfe algorithm (FW) for recovering sparse solutions to posterior inference. From detailed elucidation of both theoretical and practical aspects, FW exhibits many interesting properties which are beneficial to topic modeling. We then employ FW to design fast methods, including ML-FW, for learning latent Dirichlet allocation (LDA) at large scales. Extensive experiments show that to reach the same predictiveness level, ML-FW can perform tens to thousand times faster than existing state-of-the-art methods for learning LDA from massive/streaming data.

Probable convexity and its application to Correlated Topic Models

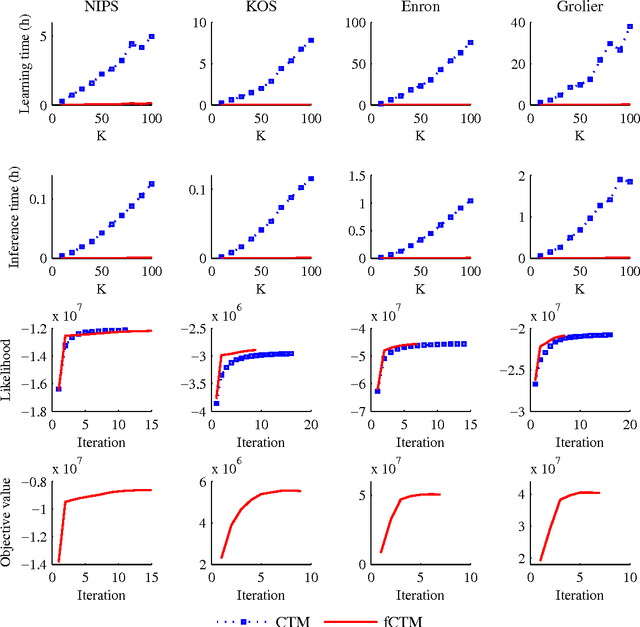
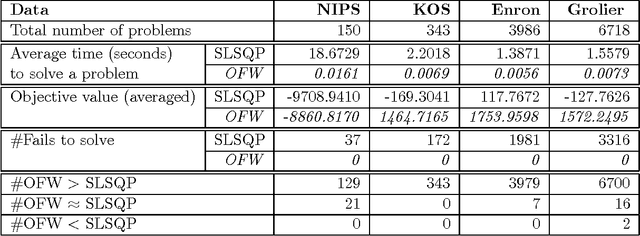
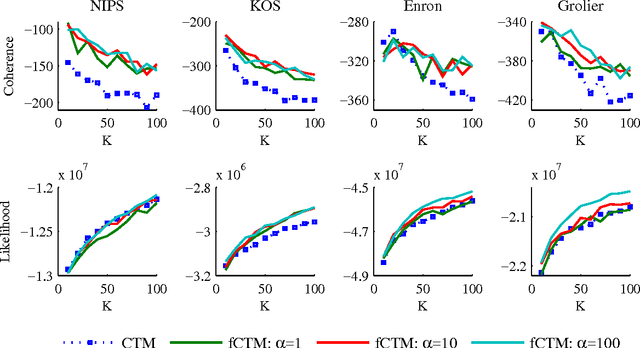
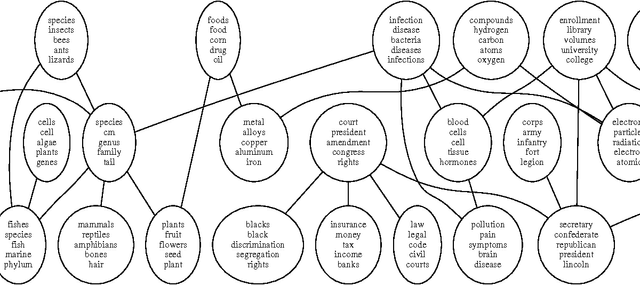
Non-convex optimization problems often arise from probabilistic modeling, such as estimation of posterior distributions. Non-convexity makes the problems intractable, and poses various obstacles for us to design efficient algorithms. In this work, we attack non-convexity by first introducing the concept of \emph{probable convexity} for analyzing convexity of real functions in practice. We then use the new concept to analyze an inference problem in the \emph{Correlated Topic Model} (CTM) and related nonconjugate models. Contrary to the existing belief of intractability, we show that this inference problem is concave under certain conditions. One consequence of our analyses is a novel algorithm for learning CTM which is significantly more scalable and qualitative than existing methods. Finally, we highlight that stochastic gradient algorithms might be a practical choice to resolve efficiently non-convex problems. This finding might find beneficial in many contexts which are beyond probabilistic modeling.

Managing sparsity, time, and quality of inference in topic models

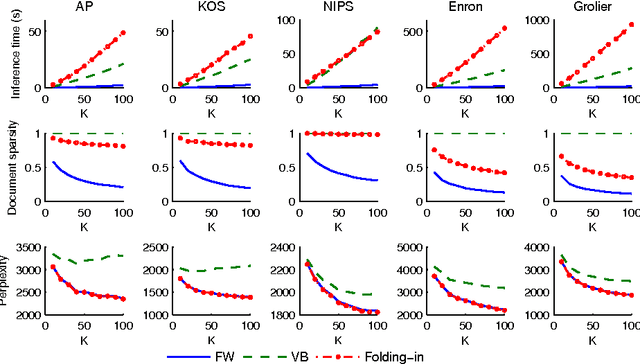
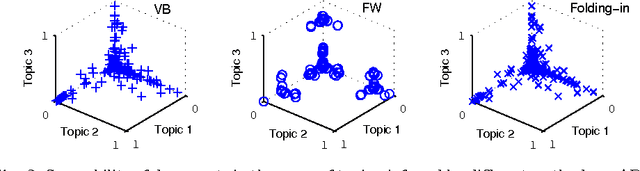
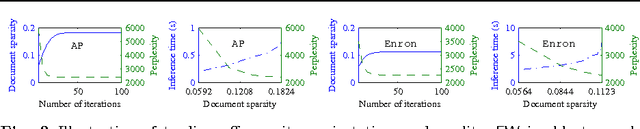
Inference is an integral part of probabilistic topic models, but is often non-trivial to derive an efficient algorithm for a specific model. It is even much more challenging when we want to find a fast inference algorithm which always yields sparse latent representations of documents. In this article, we introduce a simple framework for inference in probabilistic topic models, denoted by FW. This framework is general and flexible enough to be easily adapted to mixture models. It has a linear convergence rate, offers an easy way to incorporate prior knowledge, and provides us an easy way to directly trade off sparsity against quality and time. We demonstrate the goodness and flexibility of FW over existing inference methods by a number of tasks. Finally, we show how inference in topic models with nonconjugate priors can be done efficiently.