Sparsity exploitation via discovering graphical models in multi-variate time-series forecasting

Graph neural networks (GNNs) have been widely applied in multi-variate time-series forecasting (MTSF) tasks because of their capability in capturing the correlations among different time-series. These graph-based learning approaches improve the forecasting performance by discovering and understanding the underlying graph structures, which represent the data correlation. When the explicit prior graph structures are not available, most existing works cannot guarantee the sparsity of the generated graphs that make the overall model computational expensive and less interpretable. In this work, we propose a decoupled training method, which includes a graph generating module and a GNNs forecasting module. First, we use Graphical Lasso (or GraphLASSO) to directly exploit the sparsity pattern from data to build graph structures in both static and time-varying cases. Second, we fit these graph structures and the input data into a Graph Convolutional Recurrent Network (GCRN) to train a forecasting model. The experimental results on three real-world datasets show that our novel approach has competitive performance against existing state-of-the-art forecasting algorithms while providing sparse, meaningful and explainable graph structures and reducing training time by approximately 40%. Our PyTorch implementation is publicly available at https://github.com/HySonLab/GraphLASSO

Fast Parallel Randomized Algorithm for Nonnegative Matrix Factorization with KL Divergence for Large Sparse Datasets

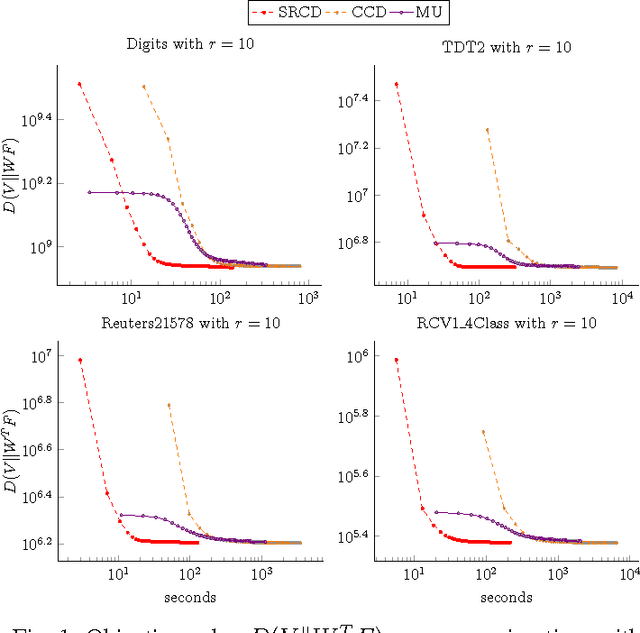
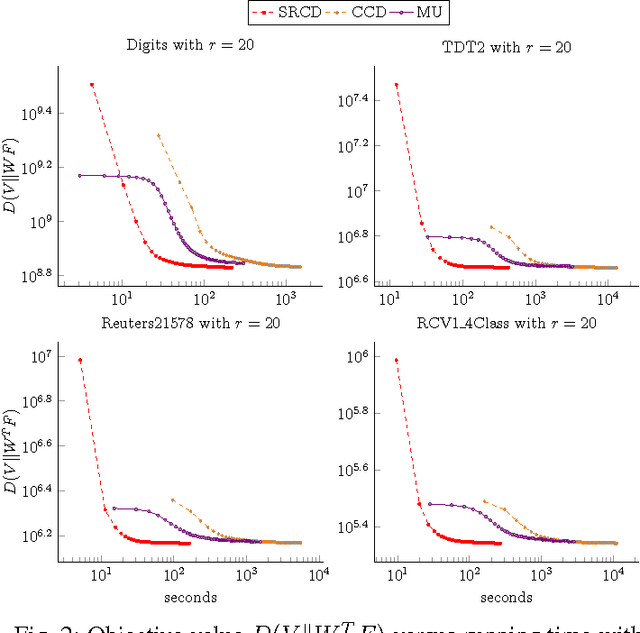
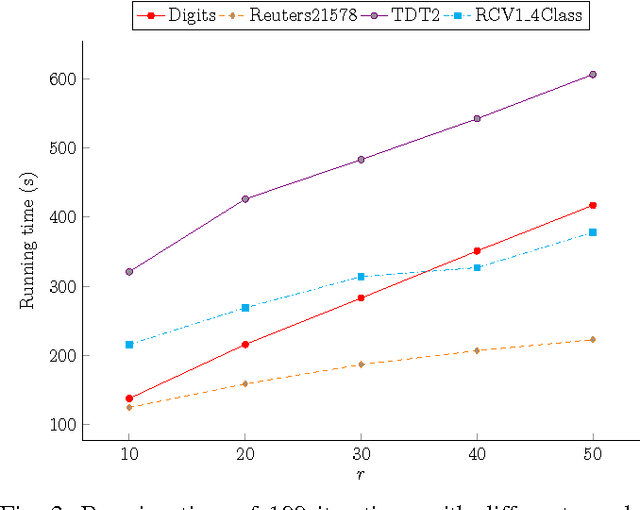
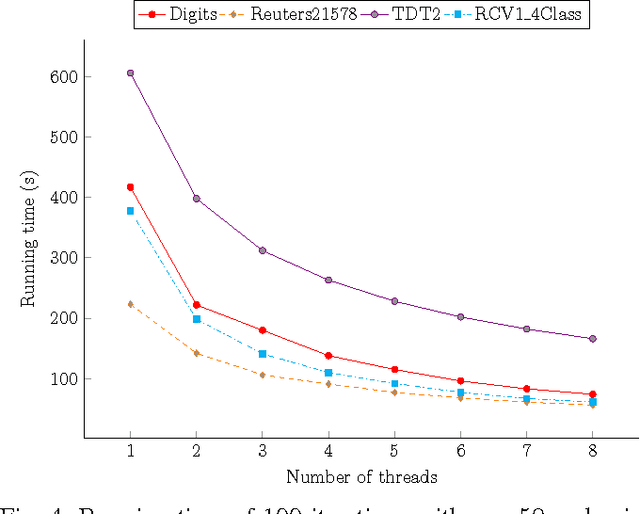
Nonnegative Matrix Factorization (NMF) with Kullback-Leibler Divergence (NMF-KL) is one of the most significant NMF problems and equivalent to Probabilistic Latent Semantic Indexing (PLSI), which has been successfully applied in many applications. For sparse count data, a Poisson distribution and KL divergence provide sparse models and sparse representation, which describe the random variation better than a normal distribution and Frobenius norm. Specially, sparse models provide more concise understanding of the appearance of attributes over latent components, while sparse representation provides concise interpretability of the contribution of latent components over instances. However, minimizing NMF with KL divergence is much more difficult than minimizing NMF with Frobenius norm; and sparse models, sparse representation and fast algorithms for large sparse datasets are still challenges for NMF with KL divergence. In this paper, we propose a fast parallel randomized coordinate descent algorithm having fast convergence for large sparse datasets to archive sparse models and sparse representation. The proposed algorithm's experimental results overperform the current studies' ones in this problem.