Efficient Bit Labeling in Factorization Machines with Annealing for Traveling Salesman Problem

To efficiently find an optimum parameter combination in a large-scale problem, it is a key to convert the parameters into available variables in actual machines. Specifically, quadratic unconstrained binary optimization problems are solved with the help of machine learning, e.g., factorization machines with annealing, which convert a raw parameter to binary variables. This work investigates the dependence of the convergence speed and the accuracy on binary labeling method, which can influence the cost function shape and thus the probability of being captured at a local minimum solution. By exemplifying traveling salesman problem, we propose and evaluate Gray labeling, which correlates the Hamming distance in binary labels with the traveling distance. Through numerical simulation of traveling salesman problem up to 15 cities at a limited number of iterations, the Gray labeling shows less local minima percentages and shorter traveling distances compared with natural labeling.

Compressed Shaping: Concept and FPGA Demonstration

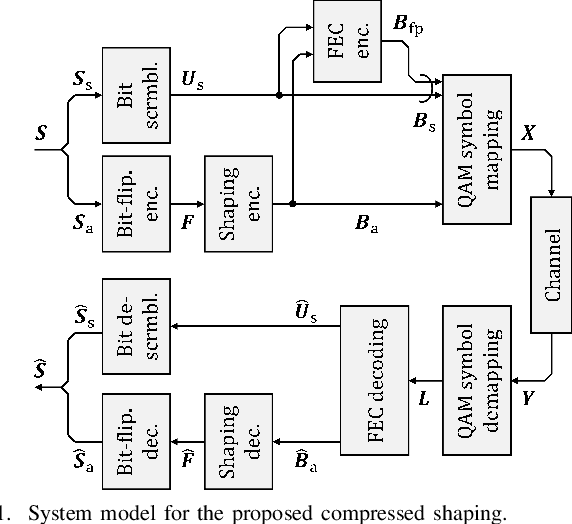
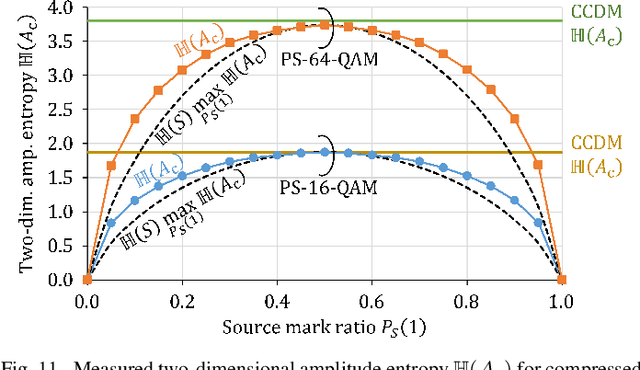
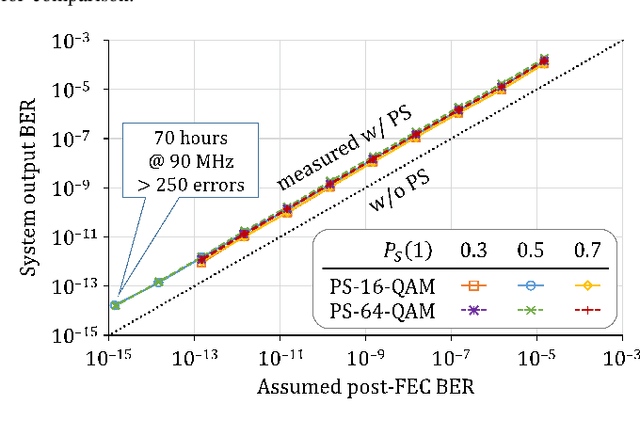
Probabilistic shaping (PS) has been widely studied and applied to optical fiber communications. The encoder of PS expends the number of bit slots and controls the probability distribution of channel input symbols. Not only studies focused on PS but also most works on optical fiber communications have assumed source uniformity (i.e. equal probability of marks and spaces) so far. On the other hand, the source information is in general nonuniform, unless bit-scrambling or other source coding techniques to balance the bit probability is performed. Interestingly,one can exploit the source nonuniformity to reduce the entropy of the channel input symbols with the PS encoder, which leads to smaller required signal-to-noise ratio at a given input logic rate. This benefit is equivalent to a combination of data compression and PS, and thus we call this technique compressed shaping. In this work, we explain its theoretical background in detail, and verify the concept by both numerical simulation and a field programmable gate array (FPGA) implementation of such a system. In particular, we find that compressed shaping can reduce power consumption in forward error correction decoding by up to 90% in nonuniform source cases. The additional hardware resources required for compressed shaping are not significant compared with forward error correction coding, and a real-time back-to-back test is successfully demonstrated.