Topological Signal Processing for 3D Point Cloud Data

Our goal in this paper is to apply the topological signal processing (TSP) framework to the analysis of 3D Point Clouds (PCs) represented on simplicial complexes. Building on Discrete Exterior Calculus (DEC) theory for vector fields, we introduce higher-order Laplacian operators that enable the processing of signals over triangular meshes. Unlike traditional approaches, the proposed approach allows us to characterize both color attributes, modeled as 3D vectors on nodes, and geometry, modeled as 3D vectors on the barycenter of each triangle. Then, we show as TSP tools may efficiently be used to sample, recover and filter PCs attributes treating them as edge signals. Numerical results on synthetic PCs demonstrate accurate color reconstruction with robustness to sparse data and geometry refinement in the case of noisy PC coordinates. The proposed approach provides a topology-based representation to characterize the geometry and attributes of PCs.

Learning Dirac Spectral Transforms for Topological Signals

The Dirac operator provides a unified framework for processing signals defined over different order topological domains, such as node and edge signals. Its eigenmodes define a spectral representation that inherently captures cross-domain interactions, in contrast to conventional Hodge-Laplacian eigenmodes that operate within a single topological dimension. In this paper, we compare the two alternatives in terms of the distortion/sparsity trade-off and we show how an overcomplete basis built concatenating the two dictionaries can provide better performance with respect to each approach. Then, we propose a parameterized nonredundant transform whose eigenmodes incorporate a mode-specific mass parameter that captures the interplay between node and edge modes. Interestingly, we show that learning the mass parameters from data makes the proposed transform able to achieve the best distortion-sparsity tradeoff with respect to both complete and overcomplete bases.

Physics-Informed Topological Signal Processing for Water Distribution Network Monitoring

Water management is one of the most critical aspects of our society, together with population increase and climate change. Water scarcity requires a better characterization and monitoring of Water Distribution Networks (WDNs). This paper presents a novel framework for monitoring Water Distribution Networks (WDNs) by integrating physics-informed modeling of the nonlinear interactions between pressure and flow data with Topological Signal Processing (TSP) techniques. We represent pressure and flow data as signals defined over a second-order cell complex, enabling accurate estimation of water pressures and flows throughout the entire network from sparse sensor measurements. By formalizing hydraulic conservation laws through the TSP framework, we provide a comprehensive representation of nodal pressures and edge flows that incorporate higher-order interactions captured through the formalism of cell complexes. This provides a principled way to decompose the water flows in WDNs in three orthogonal signal components (irrotational, solenoidal and harmonic). The spectral representations of these components inherently reflect the conservation laws governing the water pressures and flows. Sparse representation in the spectral domain enable topology-based sampling and reconstruction of nodal pressures and water flows from sparse measurements. Our results demonstrate that employing cell complex-based signal representations enhances the accuracy of edge signal reconstruction, due to proper modeling of both conservative and non-conservative flows along the polygonal cells.

Improving J-divergence of brain connectivity states by graph Laplacian denoising

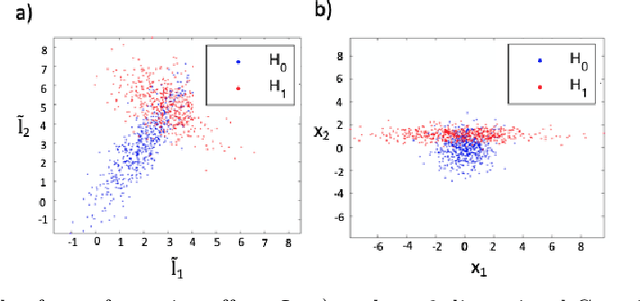
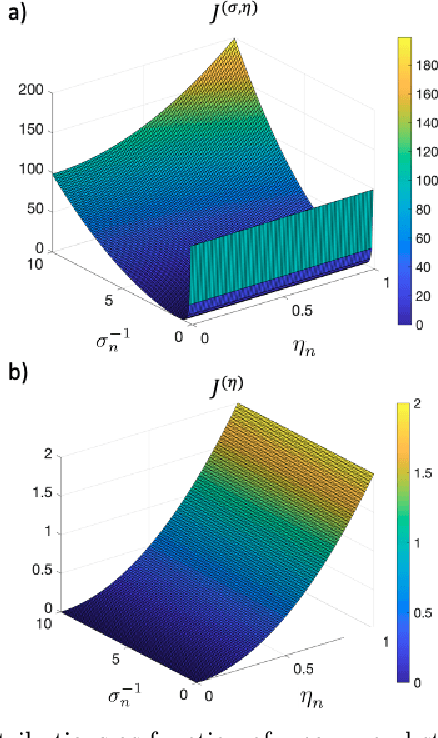
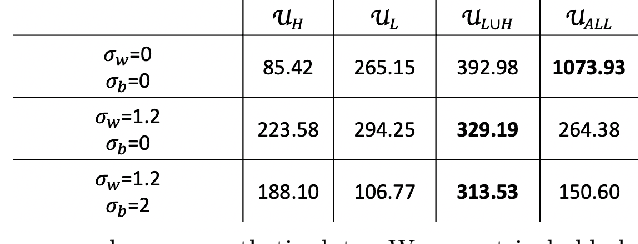
Functional connectivity (FC) can be represented as a network, and is frequently used to better understand the neural underpinnings of complex tasks such as motor imagery (MI) detection in brain-computer interfaces (BCIs). However, errors in the estimation of connectivity can affect the detection performances. In this work, we address the problem of denoising common connectivity estimates to improve the detectability of different connectivity states. Specifically, we propose a denoising algorithm that acts on the network graph Laplacian, which leverages recent graph signal processing results. Further, we derive a novel formulation of the Jensen divergence for the denoised Laplacian under different states. Numerical simulations on synthetic data show that the denoising method improves the Jensen divergence of connectivity patterns corresponding to different task conditions. Furthermore, we apply the Laplacian denoising technique to brain networks estimated from real EEG data recorded during MI-BCI experiments. Using our novel formulation of the J-divergence, we are able to quantify the distance between the FC networks in the motor imagery and resting states, as well as to understand the contribution of each Laplacian variable to the total J-divergence between two states. Experimental results on real MI-BCI EEG data demonstrate that the Laplacian denoising improves the separation of motor imagery and resting mental states, and shortens the time interval required for connectivity estimation. We conclude that the approach shows promise for the robust detection of connectivity states while being appealing for implementation in real-time BCI applications.