Condensation-Concatenation Framework for Dynamic Graph Continual Learning

Dynamic graphs are prevalent in real-world scenarios, where continuous structural changes induce catastrophic forgetting in graph neural networks (GNNs). While continual learning has been extended to dynamic graphs, existing methods overlook the effects of topological changes on existing nodes. To address it, we propose a novel framework for continual learning on dynamic graphs, named Condensation-Concatenation-based Continual Learning (CCC). Specifically, CCC first condenses historical graph snapshots into compact semantic representations while aiming to preserve the original label distribution and topological properties. Then it concatenates these historical embeddings with current graph representations selectively. Moreover, we refine the forgetting measure (FM) to better adapt to dynamic graph scenarios by quantifying the predictive performance degradation of existing nodes caused by structural updates. CCC demonstrates superior performance over state-of-the-art baselines across four real-world datasets in extensive experiments.

On Tsallis Entropy Bias and Generalized Maximum Entropy Models

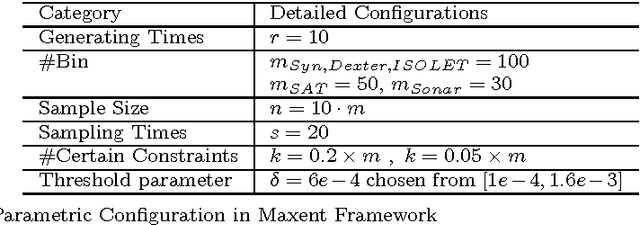
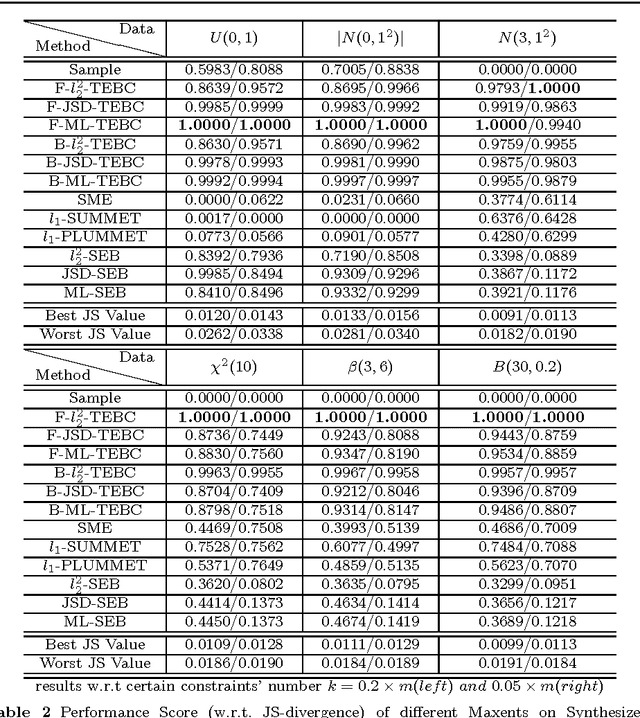
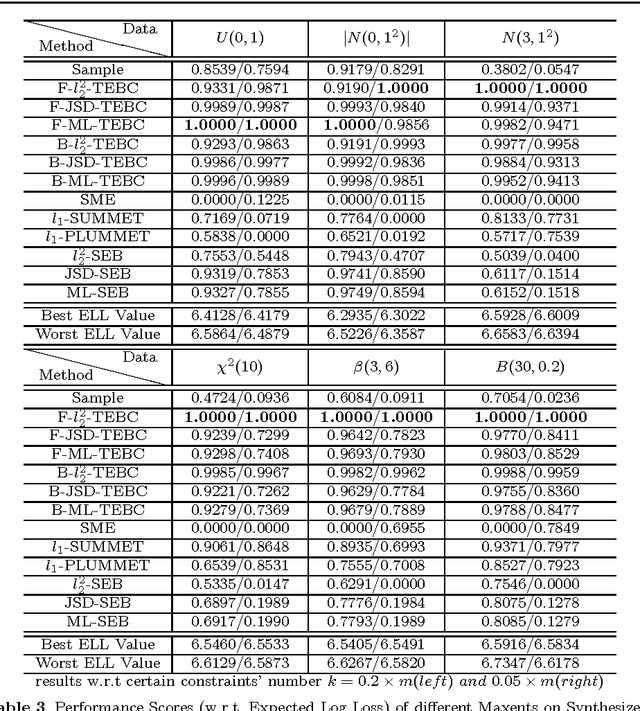
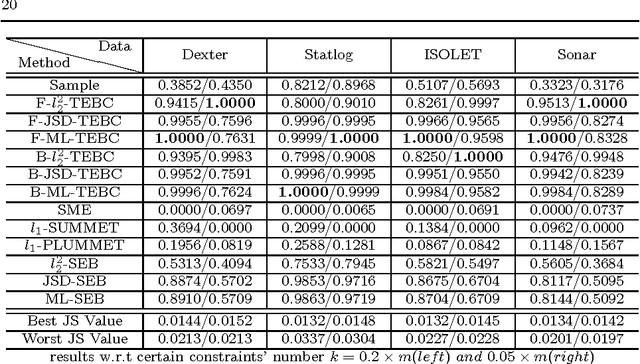
In density estimation task, maximum entropy model (Maxent) can effectively use reliable prior information via certain constraints, i.e., linear constraints without empirical parameters. However, reliable prior information is often insufficient, and the selection of uncertain constraints becomes necessary but poses considerable implementation complexity. Improper setting of uncertain constraints can result in overfitting or underfitting. To solve this problem, a generalization of Maxent, under Tsallis entropy framework, is proposed. The proposed method introduces a convex quadratic constraint for the correction of (expected) Tsallis entropy bias (TEB). Specifically, we demonstrate that the expected Tsallis entropy of sampling distributions is smaller than the Tsallis entropy of the underlying real distribution. This expected entropy reduction is exactly the (expected) TEB, which can be expressed by a closed-form formula and act as a consistent and unbiased correction. TEB indicates that the entropy of a specific sampling distribution should be increased accordingly. This entails a quantitative re-interpretation of the Maxent principle. By compensating TEB and meanwhile forcing the resulting distribution to be close to the sampling distribution, our generalized TEBC Maxent can be expected to alleviate the overfitting and underfitting. We also present a connection between TEB and Lidstone estimator. As a result, TEB-Lidstone estimator is developed by analytically identifying the rate of probability correction in Lidstone. Extensive empirical evaluation shows promising performance of both TEBC Maxent and TEB-Lidstone in comparison with various state-of-the-art density estimation methods.