Fine-tune Language Models to Approximate Unbiased In-context Learning

In-context learning (ICL) is an astonishing emergent ability of large language models (LLMs). By presenting a prompt that includes multiple input-output pairs as examples and introducing a new query input, models can generate the corresponding output. However, the performance of models heavily relies on the quality of the input prompt when implementing in-context learning. Biased or imbalanced input prompts can significantly degrade the performance of language models. To address this issue, we introduce a reweighted algorithm called RICL (Reweighted In-context Learning). This algorithm fine-tunes language models using an unbiased validation set to determine the optimal weight for each input-output example to approximate unbiased in-context learning. Furthermore, we also introduce a low-cost reweighted algorithm, a linear optimal weight approximation algorithm called LARICL (Linear Approximation of Reweighted In-context Learning). This algorithm requires minimal training cost while providing effective results. We prove the convergence of our algorithm and validate its performance through experiments conducted on a numerical dataset. The experimental findings reveal a substantial improvement in comparison to benchmarks including the performance of casual prompt-based in-context learning and the performance of a classic fine-tuning method.

How to Protect Copyright Data in Optimization of Large Language Models?

Large language models (LLMs) and generative AI have played a transformative role in computer research and applications. Controversy has arisen as to whether these models output copyrighted data, which can occur if the data the models are trained on is copyrighted. LLMs are built on the transformer neural network architecture, which in turn relies on a mathematical computation called Attention that uses the softmax function. In this paper, we show that large language model training and optimization can be seen as a softmax regression problem. We then establish a method of efficiently performing softmax regression, in a way that prevents the regression function from generating copyright data. This establishes a theoretical method of training large language models in a way that avoids generating copyright data.

Spectral Clustering on Large Datasets: When Does it Work? Theory from Continuous Clustering and Density Cheeger-Buser

Spectral clustering is one of the most popular clustering algorithms that has stood the test of time. It is simple to describe, can be implemented using standard linear algebra, and often finds better clusters than traditional clustering algorithms like $k$-means and $k$-centers. The foundational algorithm for two-way spectral clustering, by Shi and Malik, creates a geometric graph from data and finds a spectral cut of the graph. In modern machine learning, many data sets are modeled as a large number of points drawn from a probability density function. Little is known about when spectral clustering works in this setting -- and when it doesn't. Past researchers justified spectral clustering by appealing to the graph Cheeger inequality (which states that the spectral cut of a graph approximates the ``Normalized Cut''), but this justification is known to break down on large data sets. We provide theoretically-informed intuition about spectral clustering on large data sets drawn from probability densities, by proving when a continuous form of spectral clustering considered by past researchers (the unweighted spectral cut of a probability density) finds good clusters of the underlying density itself. Our work suggests that Shi-Malik spectral clustering works well on data drawn from mixtures of Laplace distributions, and works poorly on data drawn from certain other densities, such as a density we call the `square-root trough'. Our core theorem proves that weighted spectral cuts have low weighted isoperimetry for all probability densities. Our key tool is a new Cheeger-Buser inequality for all probability densities, including discontinuous ones.

Functions that Preserve Manhattan Distances

What functions, when applied to the pairwise Manhattan distances between any $n$ points, result in the Manhattan distances between another set of $n$ points? In this paper, we show that a function has this property if and only if it is Bernstein. This class of functions admits several classical analytic characterizations and includes $f(x) = x^s$ for $0 \leq s \leq 1$ as well as $f(x) = 1-e^{-xt}$ for any $t \geq 0$. While it was previously known that Bernstein functions had this property, it was not known that these were the only such functions. Our results are a natural extension of the work of Schoenberg from 1938, who addressed this question for Euclidean distances. Schoenberg's work has been applied in probability theory, harmonic analysis, machine learning, theoretical computer science, and more. We additionally show that if and only if $f$ is completely monotone, there exists \mbox{$F:\ell_1 \rightarrow \mathbb{R}^n$} for any $x_1, \ldots x_n \in \ell_1$ such that $f(\|x_i - x_j\|_1) = \langle F(x_i), F(x_j) \rangle$. Previously, it was known that completely monotone functions had this property, but it was not known they were the only such functions. The same result but with negative type distances instead of $\ell_1$ is the foundation of all kernel methods in machine learning, and was proven by Schoenberg in 1942.

Algorithms and Hardness for Linear Algebra on Geometric Graphs

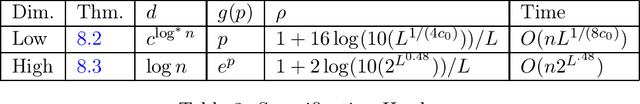
For a function $\mathsf{K} : \mathbb{R}^{d} \times \mathbb{R}^{d} \to \mathbb{R}_{\geq 0}$, and a set $P = \{ x_1, \ldots, x_n\} \subset \mathbb{R}^d$ of $n$ points, the $\mathsf{K}$ graph $G_P$ of $P$ is the complete graph on $n$ nodes where the weight between nodes $i$ and $j$ is given by $\mathsf{K}(x_i, x_j)$. In this paper, we initiate the study of when efficient spectral graph theory is possible on these graphs. We investigate whether or not it is possible to solve the following problems in $n^{1+o(1)}$ time for a $\mathsf{K}$-graph $G_P$ when $d < n^{o(1)}$: $\bullet$ Multiply a given vector by the adjacency matrix or Laplacian matrix of $G_P$ $\bullet$ Find a spectral sparsifier of $G_P$ $\bullet$ Solve a Laplacian system in $G_P$'s Laplacian matrix For each of these problems, we consider all functions of the form $\mathsf{K}(u,v) = f(\|u-v\|_2^2)$ for a function $f:\mathbb{R} \rightarrow \mathbb{R}$. We provide algorithms and comparable hardness results for many such $\mathsf{K}$, including the Gaussian kernel, Neural tangent kernels, and more. For example, in dimension $d = \Omega(\log n)$, we show that there is a parameter associated with the function $f$ for which low parameter values imply $n^{1+o(1)}$ time algorithms for all three of these problems and high parameter values imply the nonexistence of subquadratic time algorithms assuming Strong Exponential Time Hypothesis ($\mathsf{SETH}$), given natural assumptions on $f$. As part of our results, we also show that the exponential dependence on the dimension $d$ in the celebrated fast multipole method of Greengard and Rokhlin cannot be improved, assuming $\mathsf{SETH}$, for a broad class of functions $f$. To the best of our knowledge, this is the first formal limitation proven about fast multipole methods.

Weighted Cheeger and Buser Inequalities, with Applications to Clustering and Cutting Probability Densities

In this paper, we show how sparse or isoperimetric cuts of a probability density function relate to Cheeger cuts of its principal eigenfunction, for appropriate definitions of `sparse cut' and `principal eigenfunction'. We construct these appropriate definitions of sparse cut and principal eigenfunction in the probability density setting. Then, we prove Cheeger and Buser type inequalities similar to those for the normalized graph Laplacian of Alon-Milman. We demonstrate that no such inequalities hold for most prior definitions of sparse cut and principal eigenfunction. We apply this result to generate novel algorithms for cutting probability densities and clustering data, including a principled variant of spectral clustering.