Trainable Nonlinear Reaction Diffusion: A Flexible Framework for Fast and Effective Image Restoration

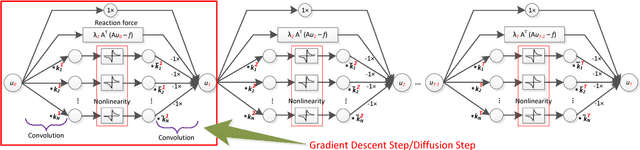
Image restoration is a long-standing problem in low-level computer vision with many interesting applications. We describe a flexible learning framework based on the concept of nonlinear reaction diffusion models for various image restoration problems. By embodying recent improvements in nonlinear diffusion models, we propose a dynamic nonlinear reaction diffusion model with time-dependent parameters (\ie, linear filters and influence functions). In contrast to previous nonlinear diffusion models, all the parameters, including the filters and the influence functions, are simultaneously learned from training data through a loss based approach. We call this approach TNRD -- \textit{Trainable Nonlinear Reaction Diffusion}. The TNRD approach is applicable for a variety of image restoration tasks by incorporating appropriate reaction force. We demonstrate its capabilities with three representative applications, Gaussian image denoising, single image super resolution and JPEG deblocking. Experiments show that our trained nonlinear diffusion models largely benefit from the training of the parameters and finally lead to the best reported performance on common test datasets for the tested applications. Our trained models preserve the structural simplicity of diffusion models and take only a small number of diffusion steps, thus are highly efficient. Moreover, they are also well-suited for parallel computation on GPUs, which makes the inference procedure extremely fast.

Real-Time Intensity-Image Reconstruction for Event Cameras Using Manifold Regularisation

Event cameras or neuromorphic cameras mimic the human perception system as they measure the per-pixel intensity change rather than the actual intensity level. In contrast to traditional cameras, such cameras capture new information about the scene at MHz frequency in the form of sparse events. The high temporal resolution comes at the cost of losing the familiar per-pixel intensity information. In this work we propose a variational model that accurately models the behaviour of event cameras, enabling reconstruction of intensity images with arbitrary frame rate in real-time. Our method is formulated on a per-event-basis, where we explicitly incorporate information about the asynchronous nature of events via an event manifold induced by the relative timestamps of events. In our experiments we verify that solving the variational model on the manifold produces high-quality images without explicitly estimating optical flow.

Total variation on a tree

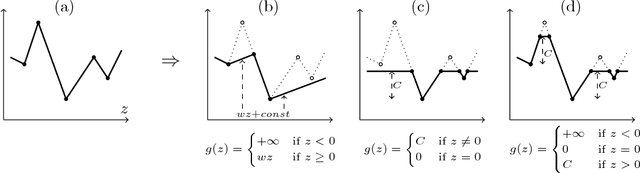
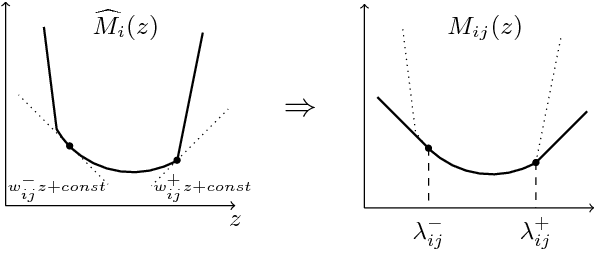
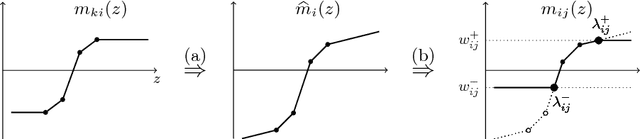
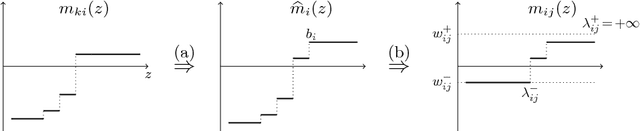
We consider the problem of minimizing the continuous valued total variation subject to different unary terms on trees and propose fast direct algorithms based on dynamic programming to solve these problems. We treat both the convex and the non-convex case and derive worst case complexities that are equal or better than existing methods. We show applications to total variation based 2D image processing and computer vision problems based on a Lagrangian decomposition approach. The resulting algorithms are very efficient, offer a high degree of parallelism and come along with memory requirements which are only in the order of the number of image pixels.

Acceleration of the PDHGM on strongly convex subspaces

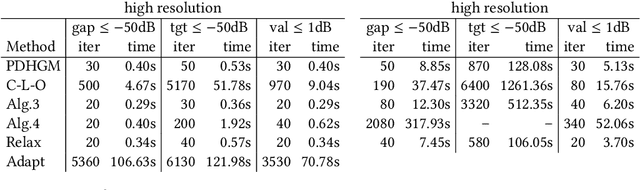
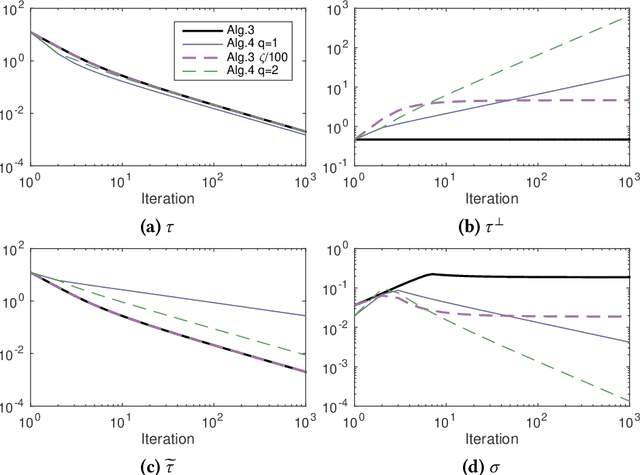
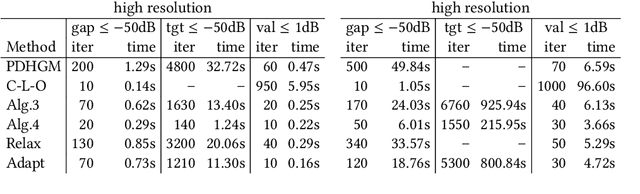
We propose several variants of the primal-dual method due to Chambolle and Pock. Without requiring full strong convexity of the objective functions, our methods are accelerated on subspaces with strong convexity. This yields mixed rates, $O(1/N^2)$ with respect to initialisation and $O(1/N)$ with respect to the dual sequence, and the residual part of the primal sequence. We demonstrate the efficacy of the proposed methods on image processing problems lacking strong convexity, such as total generalised variation denoising and total variation deblurring.

Solving Dense Image Matching in Real-Time using Discrete-Continuous Optimization

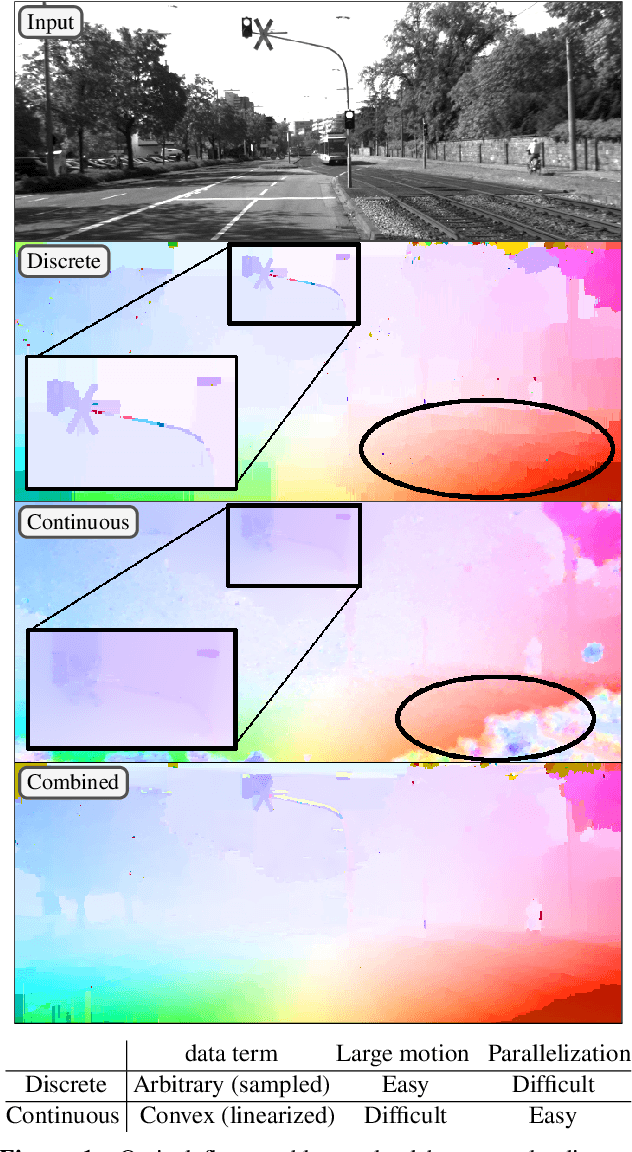
Dense image matching is a fundamental low-level problem in Computer Vision, which has received tremendous attention from both discrete and continuous optimization communities. The goal of this paper is to combine the advantages of discrete and continuous optimization in a coherent framework. We devise a model based on energy minimization, to be optimized by both discrete and continuous algorithms in a consistent way. In the discrete setting, we propose a novel optimization algorithm that can be massively parallelized. In the continuous setting we tackle the problem of non-convex regularizers by a formulation based on differences of convex functions. The resulting hybrid discrete-continuous algorithm can be efficiently accelerated by modern GPUs and we demonstrate its real-time performance for the applications of dense stereo matching and optical flow.

On learning optimized reaction diffusion processes for effective image restoration

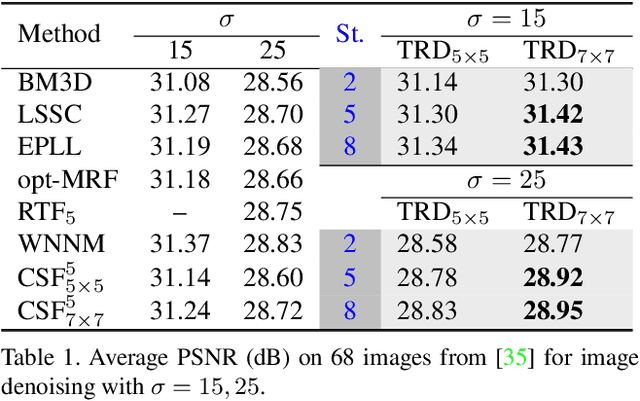
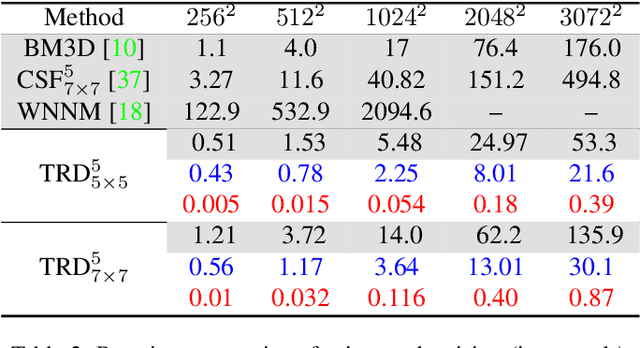
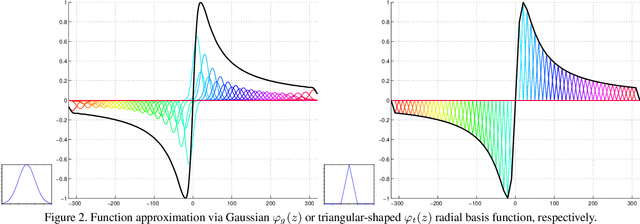
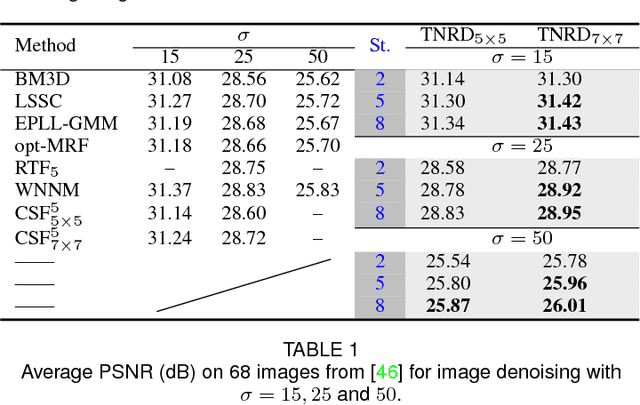
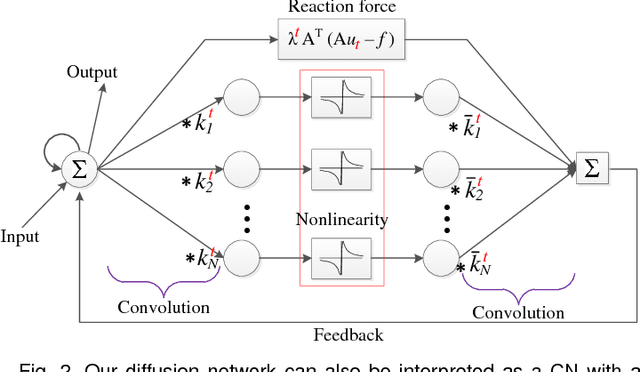
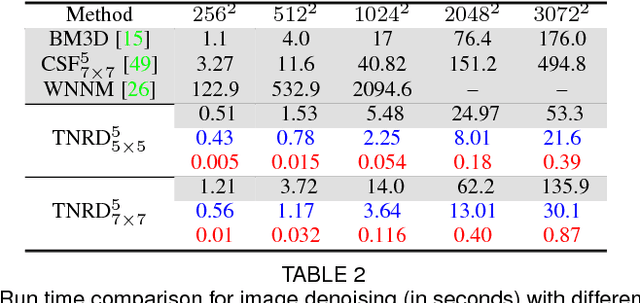
For several decades, image restoration remains an active research topic in low-level computer vision and hence new approaches are constantly emerging. However, many recently proposed algorithms achieve state-of-the-art performance only at the expense of very high computation time, which clearly limits their practical relevance. In this work, we propose a simple but effective approach with both high computational efficiency and high restoration quality. We extend conventional nonlinear reaction diffusion models by several parametrized linear filters as well as several parametrized influence functions. We propose to train the parameters of the filters and the influence functions through a loss based approach. Experiments show that our trained nonlinear reaction diffusion models largely benefit from the training of the parameters and finally lead to the best reported performance on common test datasets for image restoration. Due to their structural simplicity, our trained models are highly efficient and are also well-suited for parallel computation on GPUs.

An inertial forward-backward algorithm for monotone inclusions

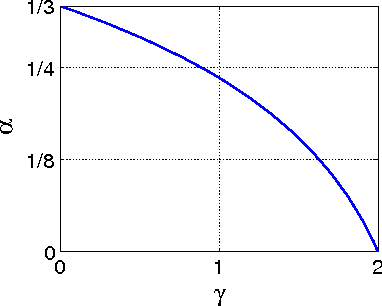
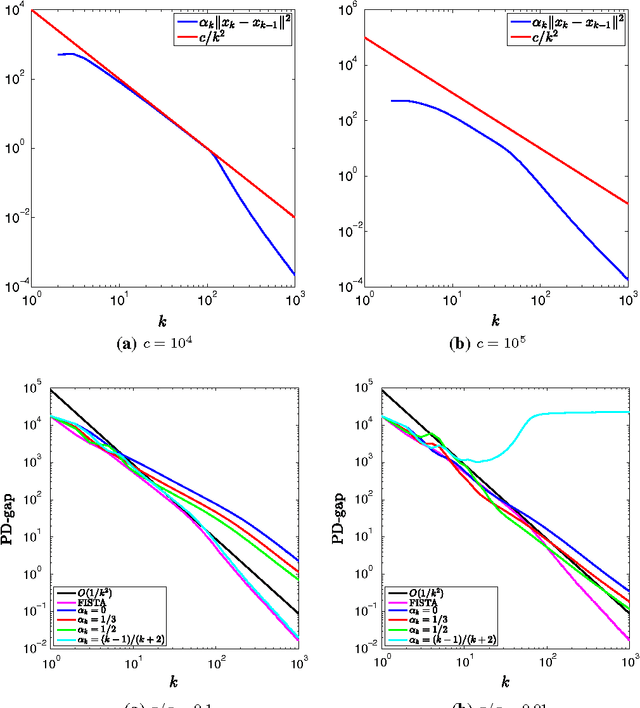
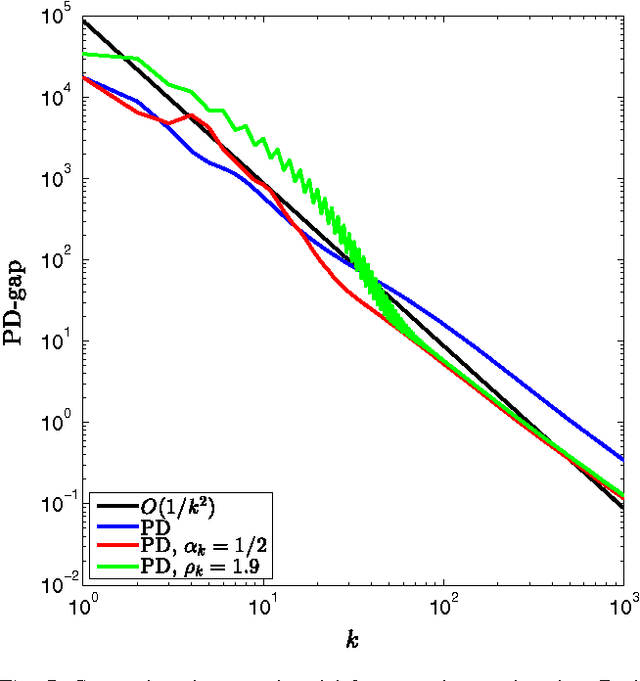
In this paper, we propose an inertial forward backward splitting algorithm to compute a zero of the sum of two monotone operators, with one of the two operators being co-coercive. The algorithm is inspired by the accelerated gradient method of Nesterov, but can be applied to a much larger class of problems including convex-concave saddle point problems and general monotone inclusions. We prove convergence of the algorithm in a Hilbert space setting and show that several recently proposed first-order methods can be obtained as special cases of the general algorithm. Numerical results show that the proposed algorithm converges faster than existing methods, while keeping the computational cost of each iteration basically unchanged.

A higher-order MRF based variational model for multiplicative noise reduction

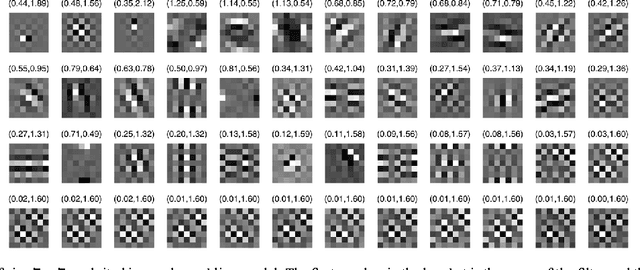
The Fields of Experts (FoE) image prior model, a filter-based higher-order Markov Random Fields (MRF) model, has been shown to be effective for many image restoration problems. Motivated by the successes of FoE-based approaches, in this letter, we propose a novel variational model for multiplicative noise reduction based on the FoE image prior model. The resulted model corresponds to a non-convex minimization problem, which can be solved by a recently published non-convex optimization algorithm. Experimental results based on synthetic speckle noise and real synthetic aperture radar (SAR) images suggest that the performance of our proposed method is on par with the best published despeckling algorithm. Besides, our proposed model comes along with an additional advantage, that the inference is extremely efficient. {Our GPU based implementation takes less than 1s to produce state-of-the-art despeckling performance.}

A bi-level view of inpainting - based image compression

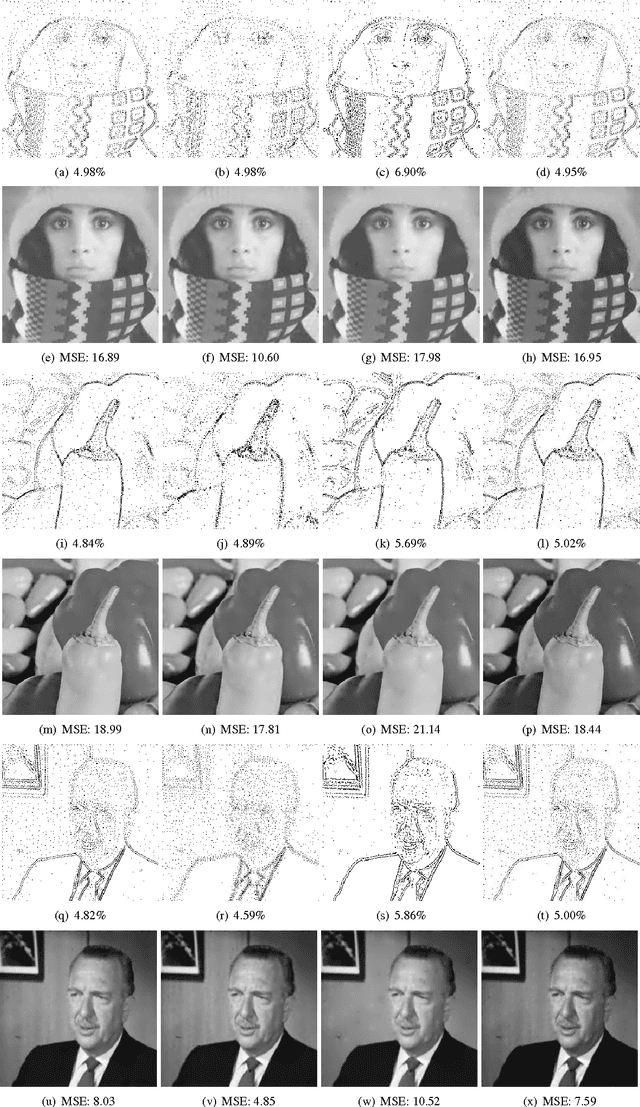
Inpainting based image compression approaches, especially linear and non-linear diffusion models, are an active research topic for lossy image compression. The major challenge in these compression models is to find a small set of descriptive supporting points, which allow for an accurate reconstruction of the original image. It turns out in practice that this is a challenging problem even for the simplest Laplacian interpolation model. In this paper, we revisit the Laplacian interpolation compression model and introduce two fast algorithms, namely successive preconditioning primal dual algorithm and the recently proposed iPiano algorithm, to solve this problem efficiently. Furthermore, we extend the Laplacian interpolation based compression model to a more general form, which is based on principles from bi-level optimization. We investigate two different variants of the Laplacian model, namely biharmonic interpolation and smoothed Total Variation regularization. Our numerical results show that significant improvements can be obtained from the biharmonic interpolation model, and it can recover an image with very high quality from only 5% pixels.

iPiano: Inertial Proximal Algorithm for Non-Convex Optimization

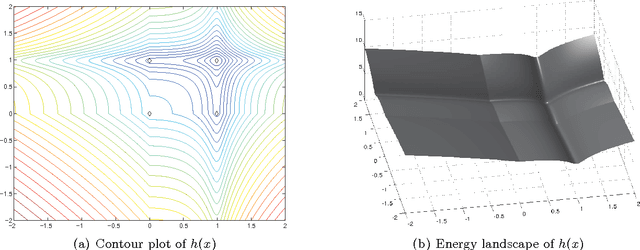
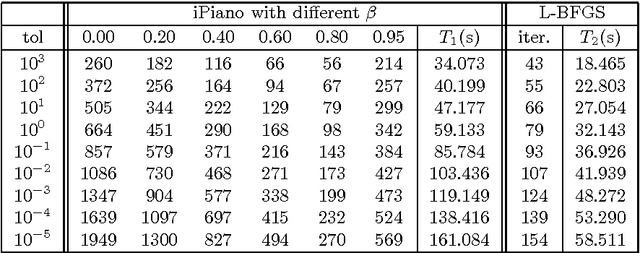
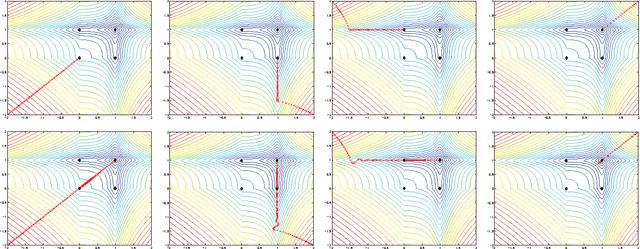
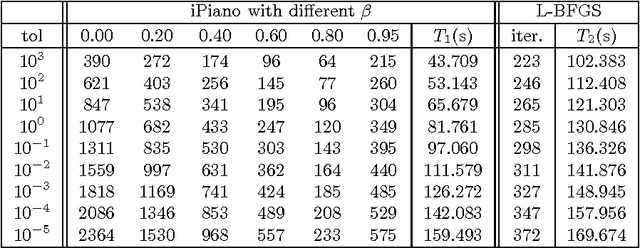
In this paper we study an algorithm for solving a minimization problem composed of a differentiable (possibly non-convex) and a convex (possibly non-differentiable) function. The algorithm iPiano combines forward-backward splitting with an inertial force. It can be seen as a non-smooth split version of the Heavy-ball method from Polyak. A rigorous analysis of the algorithm for the proposed class of problems yields global convergence of the function values and the arguments. This makes the algorithm robust for usage on non-convex problems. The convergence result is obtained based on the \KL inequality. This is a very weak restriction, which was used to prove convergence for several other gradient methods. First, an abstract convergence theorem for a generic algorithm is proved, and, then iPiano is shown to satisfy the requirements of this theorem. Furthermore, a convergence rate is established for the general problem class. We demonstrate iPiano on computer vision problems: image denoising with learned priors and diffusion based image compression.