Neural networks leverage nominally quantum and post-quantum representations

We show that deep neural networks, including transformers and RNNs, pretrained as usual on next-token prediction, intrinsically discover and represent beliefs over 'quantum' and 'post-quantum' low-dimensional generative models of their training data -- as if performing iterative Bayesian updates over the latent state of this world model during inference as they observe more context. Notably, neural nets easily find these representation whereas there is no finite classical circuit that would do the job. The corresponding geometric relationships among neural activations induced by different input sequences are found to be largely independent of neural-network architecture. Each point in this geometry corresponds to a history-induced probability density over all possible futures, and the relative displacement of these points reflects the difference in mechanism and magnitude for how these distinct pasts affect the future.

Quantum adaptive agents with efficient long-term memories

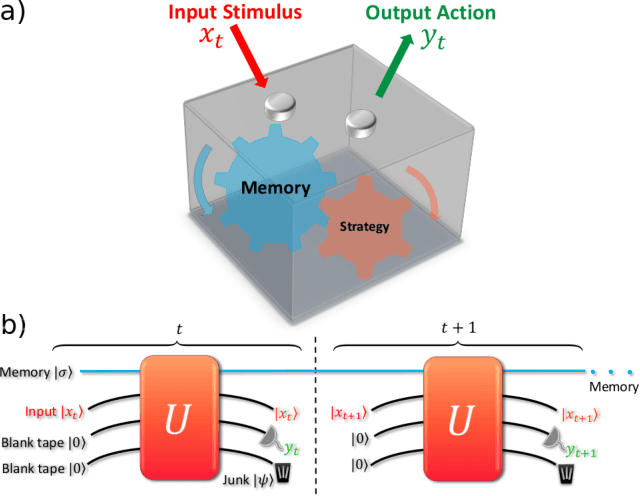
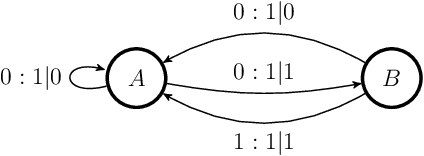
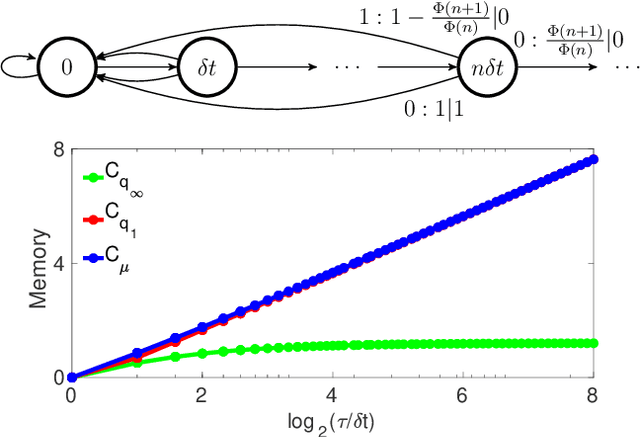
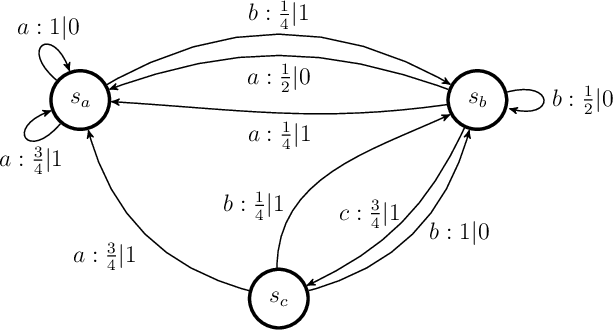
Central to the success of adaptive systems is their ability to interpret signals from their environment and respond accordingly -- they act as agents interacting with their surroundings. Such agents typically perform better when able to execute increasingly complex strategies. This comes with a cost: the more information the agent must recall from its past experiences, the more memory it will need. Here we investigate the power of agents capable of quantum information processing. We uncover the most general form a quantum agent need adopt to maximise memory compression advantages, and provide a systematic means of encoding their memory states. We show these encodings can exhibit extremely favourable scaling advantages relative to memory-minimal classical agents when information must be retained about events increasingly far into the past.

Memory compression and thermal efficiency of quantum implementations of non-deterministic hidden Markov models

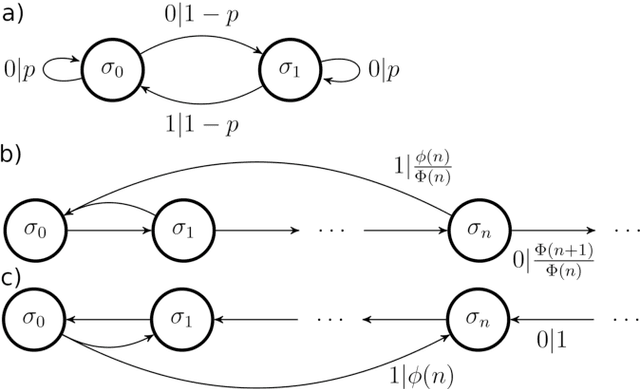
Stochastic modelling is an essential component of the quantitative sciences, with hidden Markov models (HMMs) often playing a central role. Concurrently, the rise of quantum technologies promises a host of advantages in computational problems, typically in terms of the scaling of requisite resources such as time and memory. HMMs are no exception to this, with recent results highlighting quantum implementations of deterministic HMMs exhibiting superior memory and thermal efficiency relative to their classical counterparts. In many contexts however, non-deterministic HMMs are viable alternatives; compared to them the advantages of current quantum implementations do not always hold. Here, we provide a systematic prescription for constructing quantum implementations of non-deterministic HMMs that re-establish the quantum advantages against this broader class. Crucially, we show that whenever the classical implementation suffers from thermal dissipation due to its need to process information in a time-local manner, our quantum implementations will both mitigate some of this dissipation, and achieve an advantage in memory compression.