Cooperative and Stochastic Multi-Player Multi-Armed Bandit: Optimal Regret With Neither Communication Nor Collisions

We consider the cooperative multi-player version of the stochastic multi-armed bandit problem. We study the regime where the players cannot communicate but have access to shared randomness. In prior work by the first two authors, a strategy for this regime was constructed for two players and three arms, with regret $\tilde{O}(\sqrt{T})$, and with no collisions at all between the players (with very high probability). In this paper we show that these properties (near-optimal regret and no collisions at all) are achievable for any number of players and arms. At a high level, the previous strategy heavily relied on a $2$-dimensional geometric intuition that was difficult to generalize in higher dimensions, while here we take a more combinatorial route to build the new strategy.

Coordination without communication: optimal regret in two players multi-armed bandits

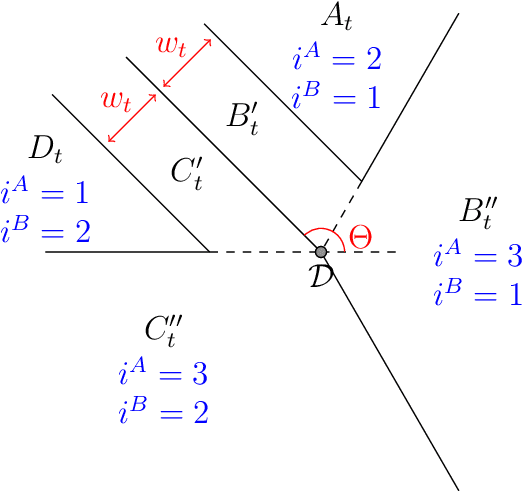
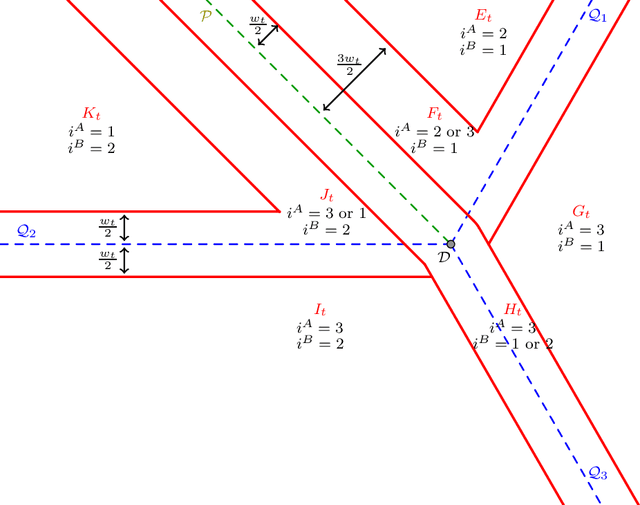
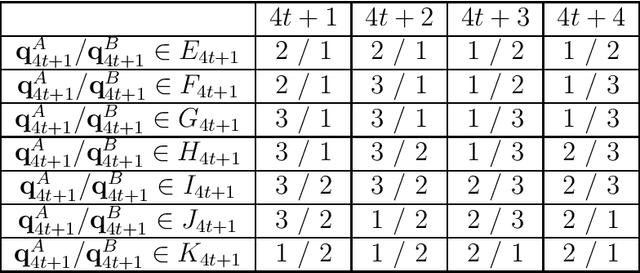
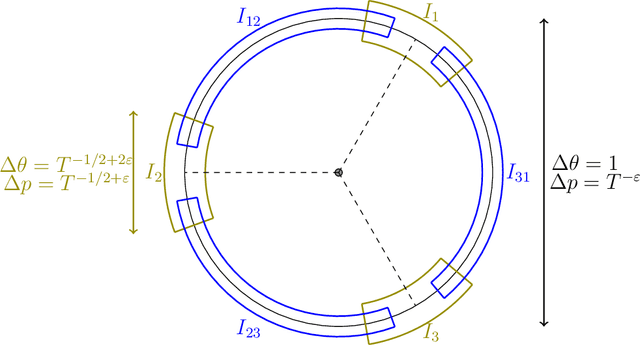
We consider two agents playing simultaneously the same stochastic three-armed bandit problem. The two agents are cooperating but they cannot communicate. We propose a strategy with no collisions at all between the players (with very high probability), and with near-optimal regret $O(\sqrt{T \log(T)})$. We also provide evidence that the extra logarithmic term $\sqrt{\log(T)}$ is necessary, with a lower bound for a variant of the problem.