Self-orthogonalizing attractor neural networks emerging from the free energy principle

Attractor dynamics are a hallmark of many complex systems, including the brain. Understanding how such self-organizing dynamics emerge from first principles is crucial for advancing our understanding of neuronal computations and the design of artificial intelligence systems. Here we formalize how attractor networks emerge from the free energy principle applied to a universal partitioning of random dynamical systems. Our approach obviates the need for explicitly imposed learning and inference rules and identifies emergent, but efficient and biologically plausible inference and learning dynamics for such self-organizing systems. These result in a collective, multi-level Bayesian active inference process. Attractors on the free energy landscape encode prior beliefs; inference integrates sensory data into posterior beliefs; and learning fine-tunes couplings to minimize long-term surprise. Analytically and via simulations, we establish that the proposed networks favor approximately orthogonalized attractor representations, a consequence of simultaneously optimizing predictive accuracy and model complexity. These attractors efficiently span the input subspace, enhancing generalization and the mutual information between hidden causes and observable effects. Furthermore, while random data presentation leads to symmetric and sparse couplings, sequential data fosters asymmetric couplings and non-equilibrium steady-state dynamics, offering a natural extension to conventional Boltzmann Machines. Our findings offer a unifying theory of self-organizing attractor networks, providing novel insights for AI and neuroscience.

Statistical quantification of confounding bias in predictive modelling

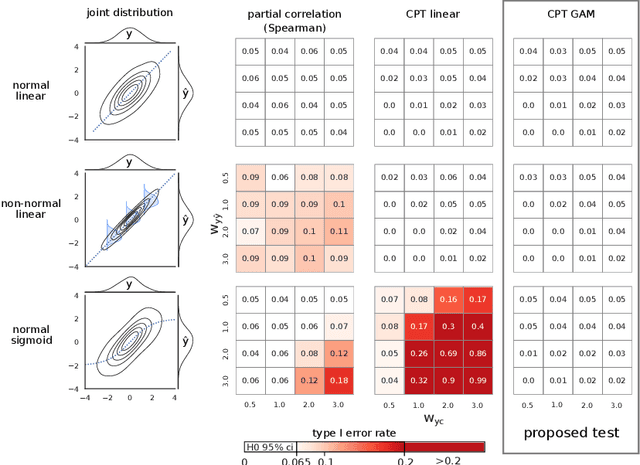
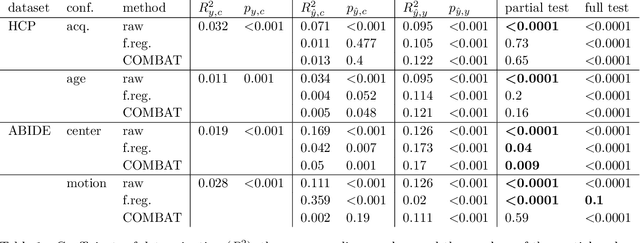
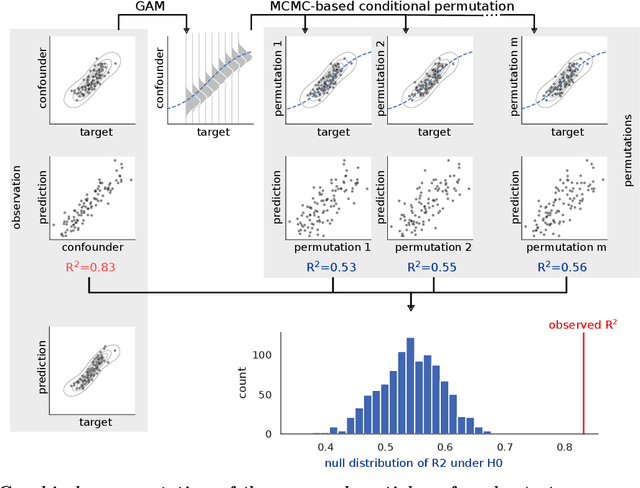
The lack of non-parametric statistical tests for confounding bias significantly hampers the development of robust, valid and generalizable predictive models in many fields of research. Here I propose the partial and full confounder tests, which, for a given confounder variable, probe the null hypotheses of unconfounded and fully confounded models, respectively. The tests provide a strict control for Type I errors and high statistical power, even for non-normally and non-linearly dependent predictions, often seen in machine learning. Applying the proposed tests on models trained on functional brain connectivity data from the Human Connectome Project and the Autism Brain Imaging Data Exchange dataset reveals confounders that were previously unreported or found to be hard to correct for with state-of-the-art confound mitigation approaches. The tests, implemented in the package mlconfound (https://mlconfound.readthedocs.io), can aid the assessment and improvement of the generalizability and neurobiological validity of predictive models and, thereby, foster the development of clinically useful machine learning biomarkers.