Target Layer Regularization for Continual Learning Using Cramer-Wold Generator

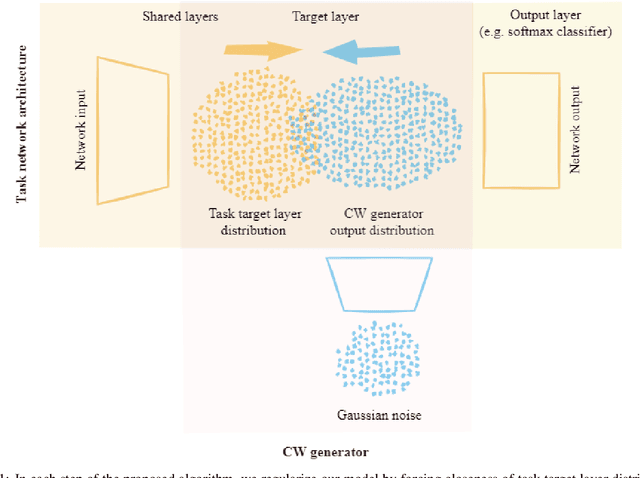
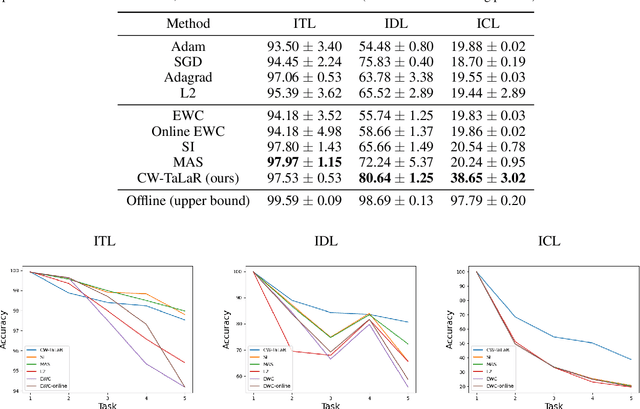
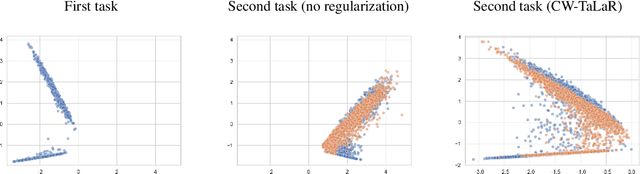
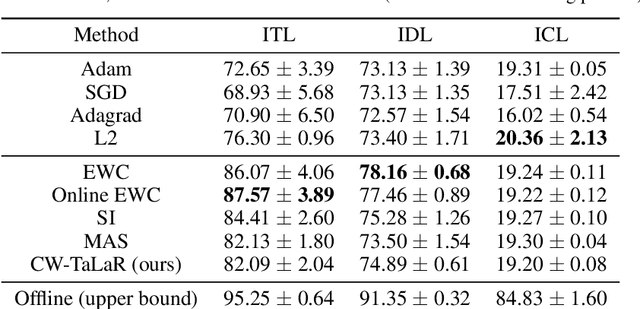
We propose an effective regularization strategy (CW-TaLaR) for solving continual learning problems. It uses a penalizing term expressed by the Cramer-Wold distance between two probability distributions defined on a target layer of an underlying neural network that is shared by all tasks, and the simple architecture of the Cramer-Wold generator for modeling output data representation. Our strategy preserves target layer distribution while learning a new task but does not require remembering previous tasks' datasets. We perform experiments involving several common supervised frameworks, which prove the competitiveness of the CW-TaLaR method in comparison to a few existing state-of-the-art continual learning models.

Generative models with kernel distance in data space

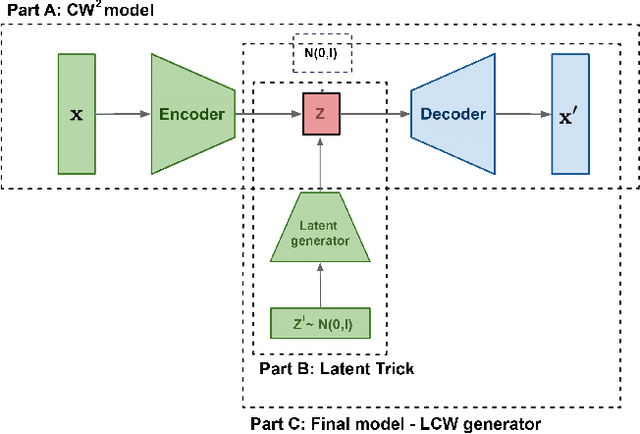
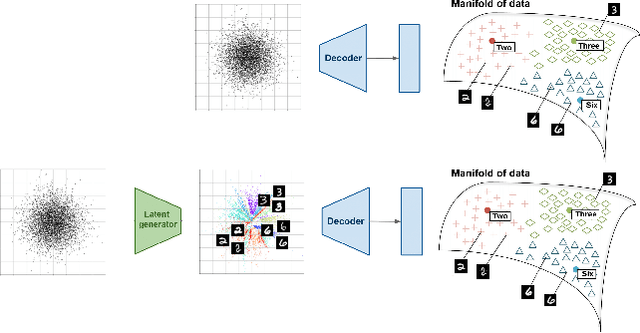
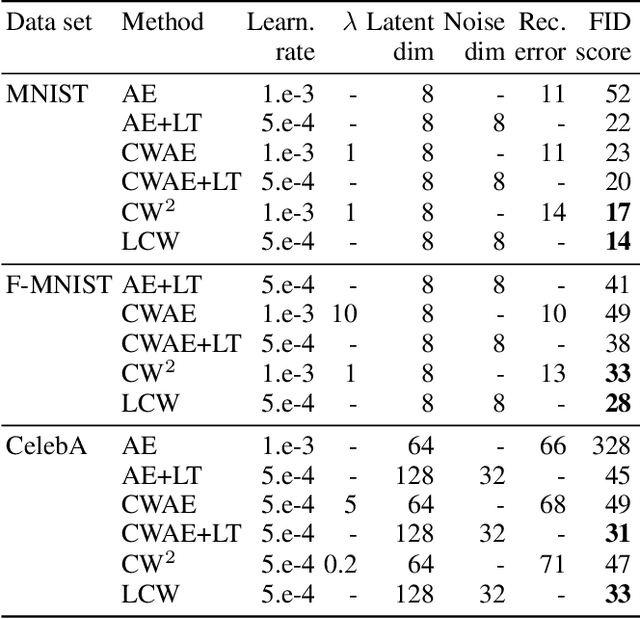
Generative models dealing with modeling a~joint data distribution are generally either autoencoder or GAN based. Both have their pros and cons, generating blurry images or being unstable in training or prone to mode collapse phenomenon, respectively. The objective of this paper is to construct a~model situated between above architectures, one that does not inherit their main weaknesses. The proposed LCW generator (Latent Cramer-Wold generator) resembles a classical GAN in transforming Gaussian noise into data space. What is of utmost importance, instead of a~discriminator, LCW generator uses kernel distance. No adversarial training is utilized, hence the name generator. It is trained in two phases. First, an autoencoder based architecture, using kernel measures, is built to model a manifold of data. We propose a Latent Trick mapping a Gaussian to latent in order to get the final model. This results in very competitive FID values.

LocoGAN -- Locally Convolutional GAN

In the paper we construct a fully convolutional GAN model: LocoGAN, which latent space is given by noise-like images of possibly different resolutions. The learning is local, i.e. we process not the whole noise-like image, but the sub-images of a fixed size. As a consequence LocoGAN can produce images of arbitrary dimensions e.g. LSUN bedroom data set. Another advantage of our approach comes from the fact that we use the position channels, which allows the generation of fully periodic (e.g. cylindrical panoramic images) or almost periodic ,,infinitely long" images (e.g. wall-papers).

One-element Batch Training by Moving Window

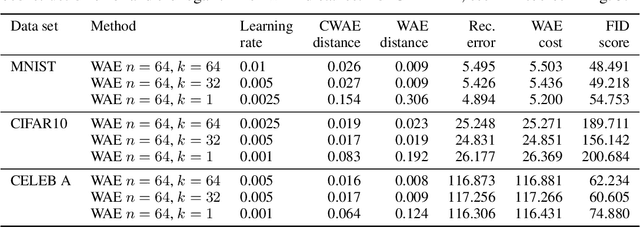
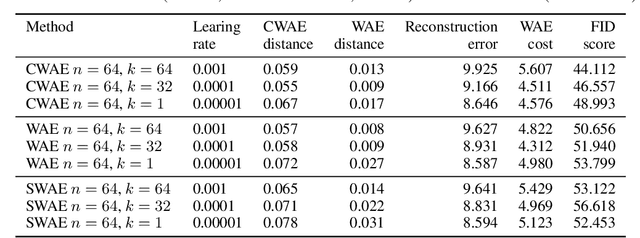
Several deep models, esp. the generative, compare the samples from two distributions (e.g. WAE like AutoEncoder models, set-processing deep networks, etc) in their cost functions. Using all these methods one cannot train the model directly taking small size (in extreme -- one element) batches, due to the fact that samples are to be compared. We propose a generic approach to training such models using one-element mini-batches. The idea is based on splitting the batch in latent into parts: previous, i.e. historical, elements used for latent space distribution matching and the current ones, used both for latent distribution computation and the minimization process. Due to the smaller memory requirements, this allows to train networks on higher resolution images then in the classical approach.

Sliced generative models

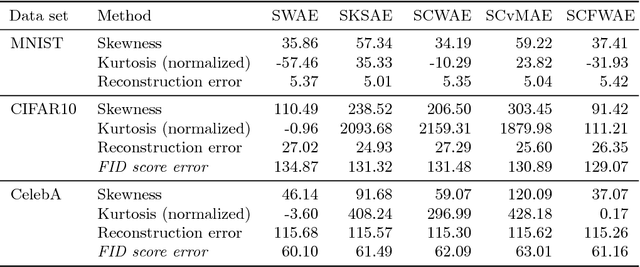
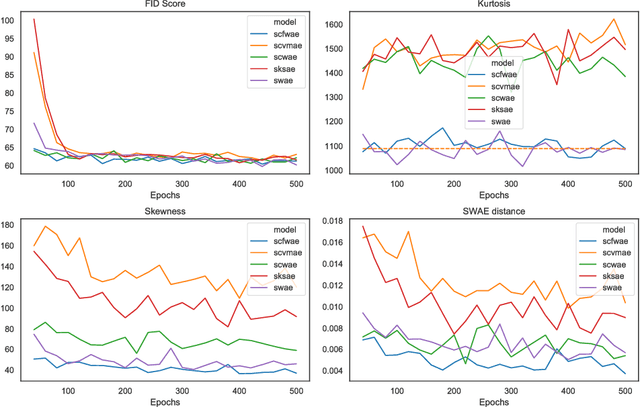
In this paper we discuss a class of AutoEncoder based generative models based on one dimensional sliced approach. The idea is based on the reduction of the discrimination between samples to one-dimensional case. Our experiments show that methods can be divided into two groups. First consists of methods which are a modification of standard normality tests, while the second is based on classical distances between samples. It turns out that both groups are correct generative models, but the second one gives a slightly faster decrease rate of Fr\'{e}chet Inception Distance (FID).

Cramer-Wold AutoEncoder

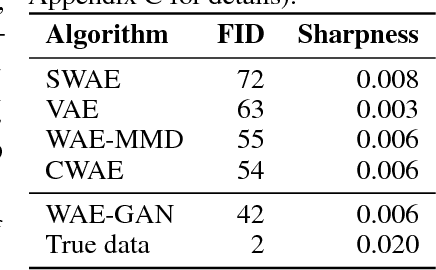
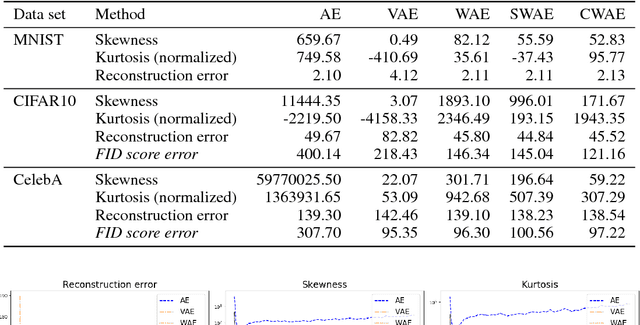
We propose a new generative model, Cramer-Wold Autoencoder (CWAE). Following WAE, we directly encourage normality of the latent space. Our paper uses also the recent idea from Sliced WAE (SWAE) model, which uses one-dimensional projections as a method of verifying closeness of two distributions. The crucial new ingredient is the introduction of a new (Cramer-Wold) metric in the space of densities, which replaces the Wasserstein metric used in SWAE. We show that the Cramer-Wold metric between Gaussian mixtures is given by a simple analytic formula, which results in the removal of sampling necessary to estimate the cost function in WAE and SWAE models. As a consequence, while drastically simplifying the optimization procedure, CWAE produces samples of a matching perceptual quality to other SOTA models.