Convergence of Mean Shift Algorithms for Large Bandwidths and Simultaneous Accurate Clustering

The mean shift (MS) is a non-parametric, density-based, iterative algorithm that has prominent usage in clustering and image segmentation. A rigorous proof for its convergence in full generality remains unknown. Two significant steps in this direction were taken in the paper \cite{Gh1}, which proved that for \textit{sufficiently large bandwidth}, the MS algorithm with the Gaussian kernel always converges in any dimension, and also by the same author in \cite{Gh2}, proved that MS always converges in one dimension for kernels with differentiable, strictly decreasing, convex profiles. In the more recent paper \cite{YT}, they have proved the convergence in more generality,\textit{ without any restriction on the bandwidth}, with the assumption that the KDE $f$ has a continuous Lipschitz gradient on the closure of the convex hull of the trajectory of the iterated sequence of the mode estimate, and also satisfies the {\L}ojasiewicz property there. The main theoretical result of this paper is a generalization of those of \cite{Gh1}, where we show that (1) for\textit{ sufficiently large bandwidth} convergence is guaranteed in any dimension with \textit{any radially symmetric and strictly positive definite kernels}. The proof uses two alternate characterizations of radially symmetric positive definite smooth kernels by Schoenberg and Bernstein \cite{Fass}, and borrows some steps from the proofs in \cite{Gh1}. Although the authors acknowledge that the result in that paper is more restrictive than that of \cite{YT} due to the lower bandwidth limit, it uses a different set of assumptions than \cite{YT}, and the proof technique is different.

Optimal bandwidth estimation for a fast manifold learning algorithm to detect circular structure in high-dimensional data

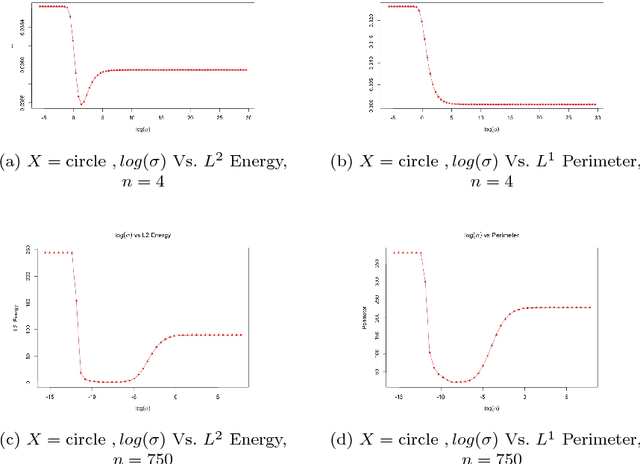
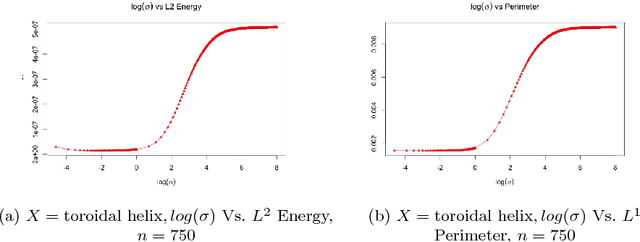
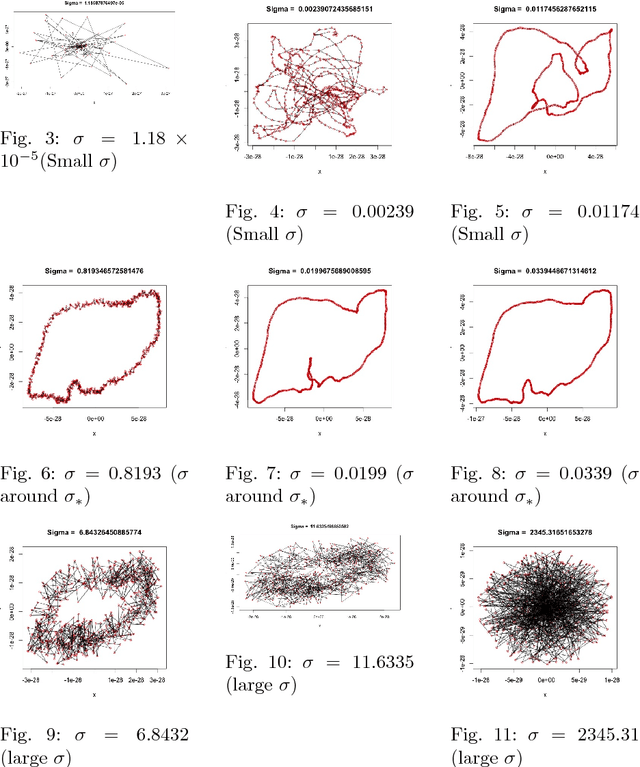
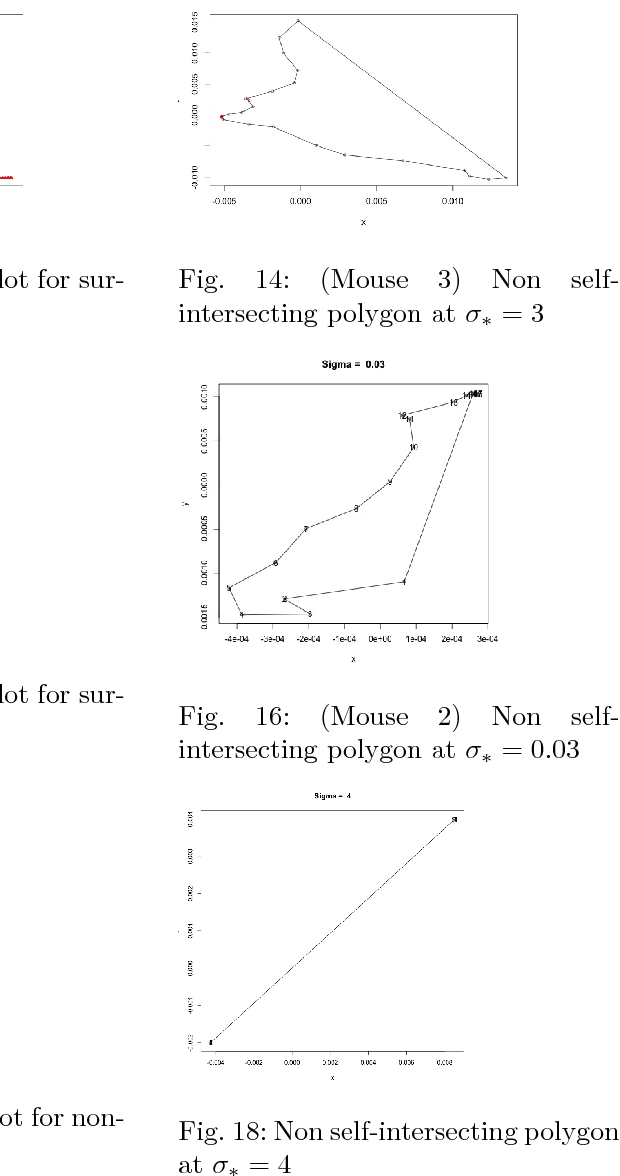
We provide a way to infer about existence of topological circularity in high-dimensional data sets in $\mathbb{R}^d$ from its projection in $\mathbb{R}^2$ obtained through a fast manifold learning map as a function of the high-dimensional dataset $\mathbb{X}$ and a particular choice of a positive real $\sigma$ known as bandwidth parameter. At the same time we also provide a way to estimate the optimal bandwidth for fast manifold learning in this setting through minimization of these functions of bandwidth. We also provide limit theorems to characterize the behavior of our proposed functions of bandwidth.