Gradient Flow Based Phase-Field Modeling Using Separable Neural Networks

The $L^2$ gradient flow of the Ginzburg-Landau free energy functional leads to the Allen Cahn equation that is widely used for modeling phase separation. Machine learning methods for solving the Allen-Cahn equation in its strong form suffer from inaccuracies in collocation techniques, errors in computing higher-order spatial derivatives through automatic differentiation, and the large system size required by the space-time approach. To overcome these limitations, we propose a separable neural network-based approximation of the phase field in a minimizing movement scheme to solve the aforementioned gradient flow problem. At each time step, the separable neural network is used to approximate the phase field in space through a low-rank tensor decomposition thereby accelerating the derivative calculations. The minimizing movement scheme naturally allows for the use of Gauss quadrature technique to compute the functional. A `$tanh$' transformation is applied on the neural network-predicted phase field to strictly bounds the solutions within the values of the two phases. For this transformation, a theoretical guarantee for energy stability of the minimizing movement scheme is established. Our results suggest that bounding the solution through this transformation is the key to effectively model sharp interfaces through separable neural network. The proposed method outperforms the state-of-the-art machine learning methods for phase separation problems and is an order of magnitude faster than the finite element method.

A Jensen-Shannon Divergence Based Loss Function for Bayesian Neural Networks

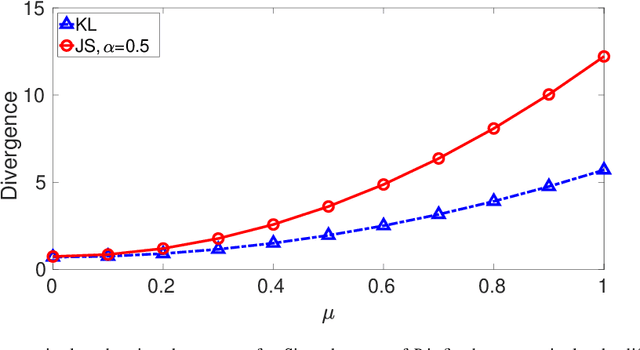
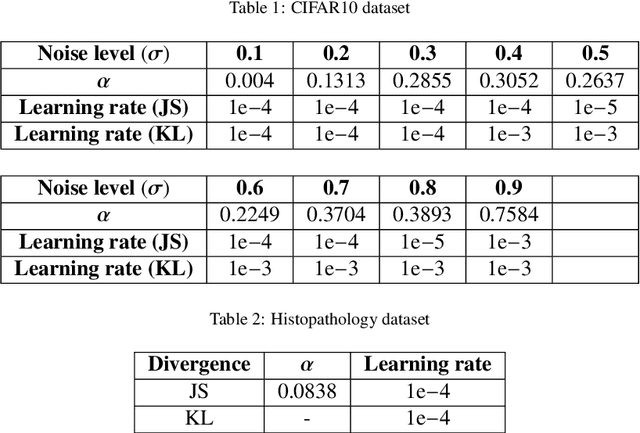
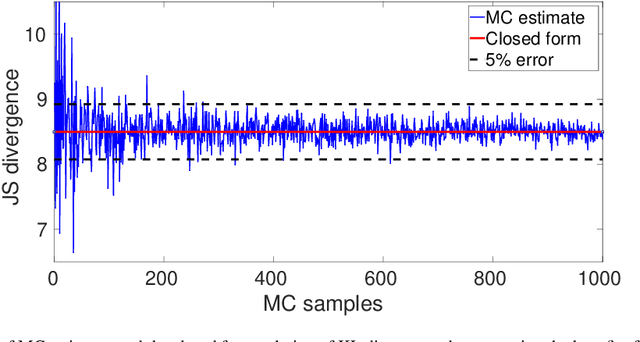
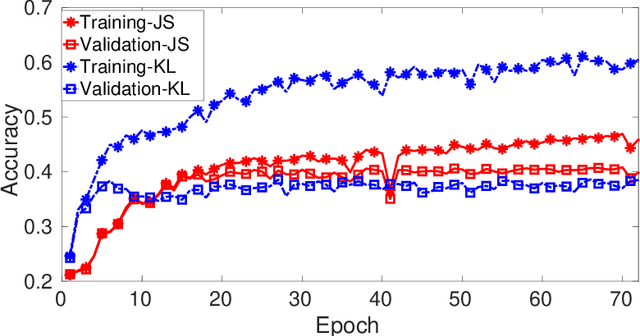
Kullback-Leibler (KL) divergence is widely used for variational inference of Bayesian Neural Networks (BNNs). However, the KL divergence has limitations such as unboundedness and asymmetry. We examine the Jensen-Shannon (JS) divergence that is more general, bounded, and symmetric. We formulate a novel loss function for BNNs based on the geometric JS divergence and show that the conventional KL divergence-based loss function is its special case. We evaluate the divergence part of the proposed loss function in a closed form for a Gaussian prior. For any other general prior, Monte Carlo approximations can be used. We provide algorithms for implementing both of these cases. We demonstrate that the proposed loss function offers an additional parameter that can be tuned to control the degree of regularisation. We derive the conditions under which the proposed loss function regularises better than the KL divergence-based loss function for Gaussian priors and posteriors. We demonstrate performance improvements over the state-of-the-art KL divergence-based BNN on the classification of a noisy CIFAR data set and a biased histopathology data set.

A modified Bayesian Convolutional Neural Network for Breast Histopathology Image Classification and Uncertainty Quantification

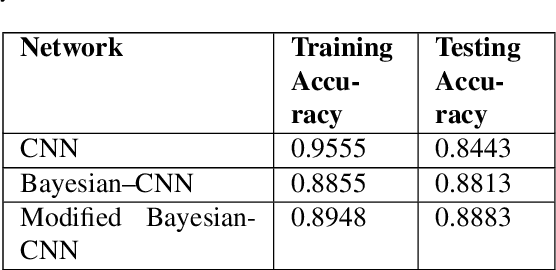
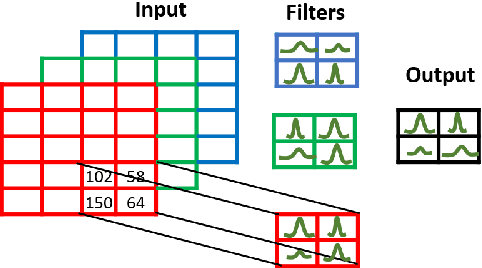
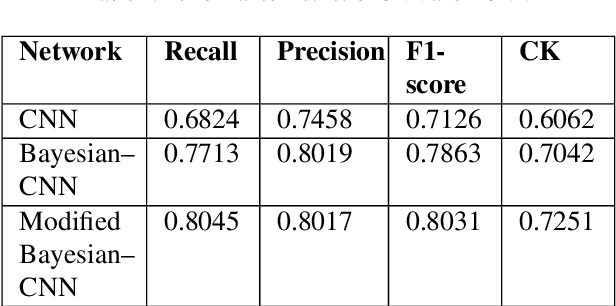
Convolutional neural network (CNN) based classification models have been successfully used on histopathological images for the detection of diseases. Despite its success, CNN may yield erroneous or overfitted results when the data is not sufficiently large or is biased. To overcome these limitations of CNN and to provide uncertainty quantification Bayesian CNN is recently proposed. However, we show that Bayesian-CNN still suffers from inaccuracies, especially in negative predictions. In the present work, we extend the Bayesian-CNN to improve accuracy and the rate of convergence. The proposed model is called modified Bayesian-CNN. The novelty of the proposed model lies in an adaptive activation function that contains a learnable parameter for each of the neurons. This adaptive activation function dynamically changes the loss function thereby providing faster convergence and better accuracy. The uncertainties associated with the predictions are obtained since the model learns a probability distribution on the network parameters. It reduces overfitting through an ensemble averaging over networks, which in turn improves accuracy on the unknown data. The proposed model demonstrates significant improvement by nearly eliminating overfitting and remarkably reducing (about 38%) the number of false-negative predictions. We found that the proposed model predicts higher uncertainty for images having features of both the classes. The uncertainty in the predictions of individual images can be used to decide when further human-expert intervention is needed. These findings have the potential to advance the state-of-the-art machine learning based automatic classification for histopathological images.