Multiview Variational Graph Autoencoders for Canonical Correlation Analysis

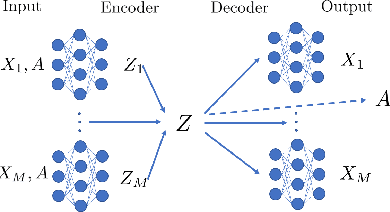
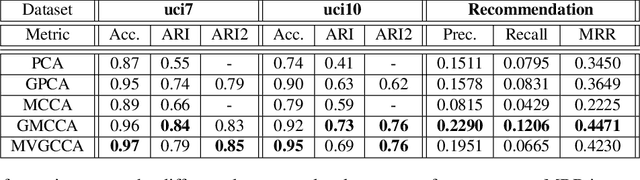
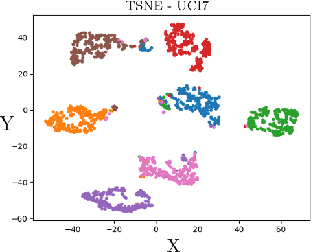
We present a novel multiview canonical correlation analysis model based on a variational approach. This is the first nonlinear model that takes into account the available graph-based geometric constraints while being scalable for processing large scale datasets with multiple views. It is based on an autoencoder architecture with graph convolutional neural network layers. We experiment with our approach on classification, clustering, and recommendation tasks on real datasets. The algorithm is competitive with state-of-the-art multiview representation learning techniques.

Graph Learning for Clustering Multi-view Data

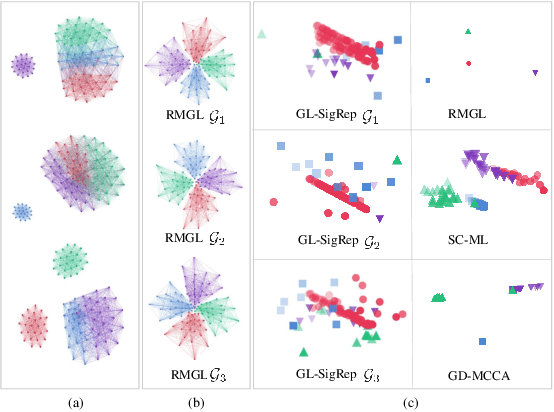
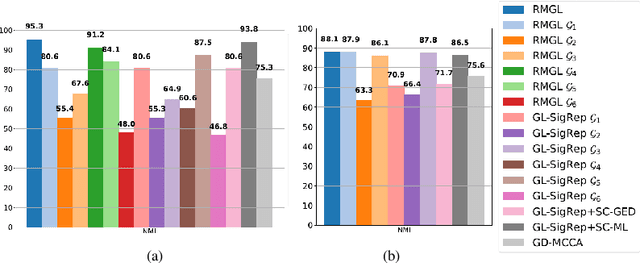
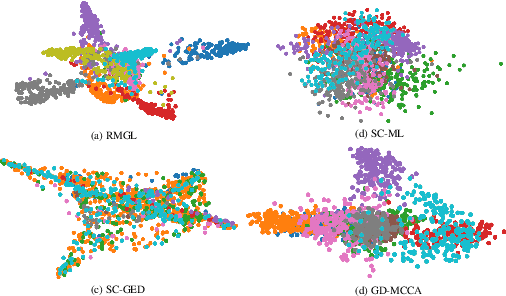
In this paper, we focus on graph learning from multi-view data of shared entities for clustering. We can explain interactions between the entities in multi-view data using a multi-layer graph with a common vertex set representing the shared entities. The edges on different layers capture the relationships of the entities. Assuming a smoothness data model, we estimate the graph Laplacian matrices of the individual graph layers by constraining their ranks to obtain multi-component graph layers for clustering. We also learn low-dimensional node embeddings, common to all the views, that assimilate the complementary information present in the views. We propose an efficient solver based on alternating minimization to solve the proposed multi-layer multi-component graph learning problem. Numerical experiments on synthetic and real datasets demonstrate that the proposed algorithm outperforms state-of-the-art multi-view clustering techniques.

Learning Sparse Graphs Under Smoothness Prior

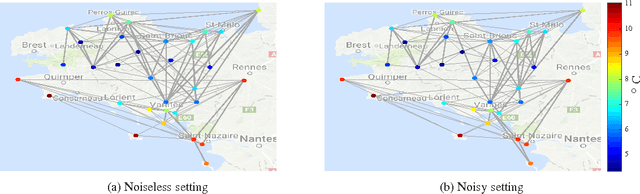
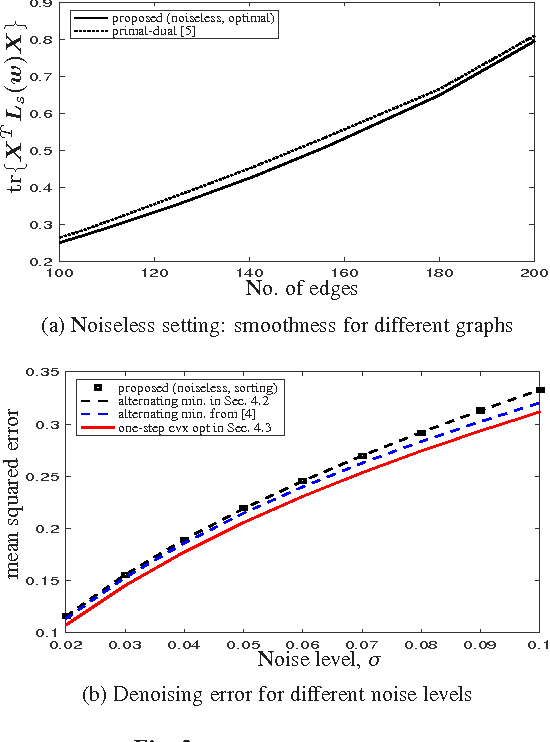
In this paper, we are interested in learning the underlying graph structure behind training data. Solving this basic problem is essential to carry out any graph signal processing or machine learning task. To realize this, we assume that the data is smooth with respect to the graph topology, and we parameterize the graph topology using an edge sampling function. That is, the graph Laplacian is expressed in terms of a sparse edge selection vector, which provides an explicit handle to control the sparsity level of the graph. We solve the sparse graph learning problem given some training data in both the noiseless and noisy settings. Given the true smooth data, the posed sparse graph learning problem can be solved optimally and is based on simple rank ordering. Given the noisy data, we show that the joint sparse graph learning and denoising problem can be simplified to designing only the sparse edge selection vector, which can be solved using convex optimization.