A First Look at Chebyshev-Sobolev Series for Digital Ink

Considering digital ink as plane curves provides a valuable framework for various applications, including signature verification, note-taking, and mathematical handwriting recognition. These plane curves can be obtained as parameterized pairs of approximating truncated series (x(s), y(s)) determined by sampled points. Earlier work has found that representing these truncated series (polynomials) in a Legendre or Legendre-Sobolev basis has a number of desirable properties. These include compact data representation, meaningful clustering of like symbols in the vector space of polynomial coefficients, linear separability of classes in this space, and highly efficient calculation of variation between curves. In this work, we take a first step at examining the use of Chebyshev-Sobolev series for symbol recognition. The early indication is that this representation may be superior to Legendre-Sobolev representation for some purposes.

Using General Large Language Models to Classify Mathematical Documents

In this article we report on an initial exploration to assess the viability of using the general large language models (LLMs), recently made public, to classify mathematical documents. Automated classification would be useful from the applied perspective of improving the navigation of the literature and the more open-ended goal of identifying relations among mathematical results. The Mathematical Subject Classification MSC 2020, from MathSciNet and zbMATH, is widely used and there is a significant corpus of ground truth material in the open literature. We have evaluated the classification of preprint articles from arXiv.org according to MSC 2020. The experiment used only the title and abstract alone -- not the entire paper. Since this was early in the use of chatbots and the development of their APIs, we report here on what was carried out by hand. Of course, the automation of the process will have to follow if it is to be generally useful. We found that in about 60% of our sample the LLM produced a primary classification matching that already reported on arXiv. In about half of those instances, there were additional primary classifications that were not detected. In about 40% of our sample, the LLM suggested a different classification than what was provided. A detailed examination of these cases, however, showed that the LLM-suggested classifications were in most cases better than those provided.

Determining Points on Handwritten Mathematical Symbols

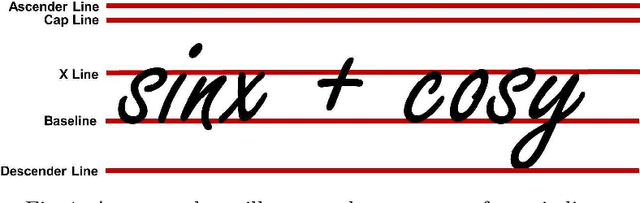
In a variety of applications, such as handwritten mathematics and diagram labelling, it is common to have symbols of many different sizes in use and for the writing not to follow simple baselines. In order to understand the scale and relative positioning of individual characters, it is necessary to identify the location of certain expected features. These are typically identified by particular points in the symbols, for example, the baseline of a lower case "p" would be identified by the lowest part of the bowl, ignoring the descender. We investigate how to find these special points automatically so they may be used in a number of problems, such as improving two-dimensional mathematical recognition and in handwriting neatening, while preserving the original style.