A data-driven approach for the closure of RANS models by the divergence of the Reynolds Stress Tensor

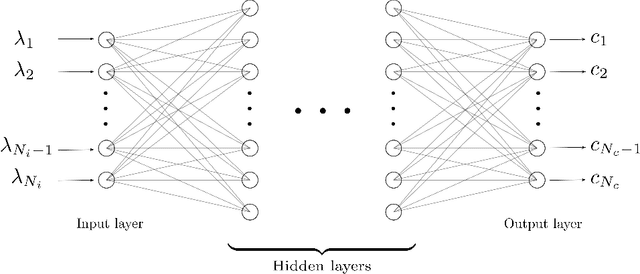
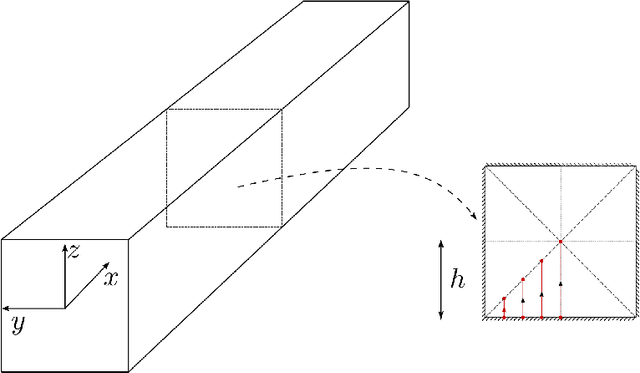
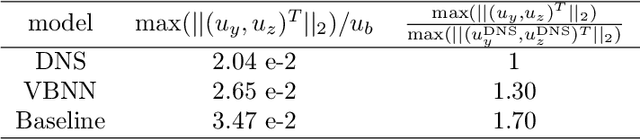
In the present paper a new data-driven model to close and increase accuracy of RANS equations is proposed. It is based on the direct approximation of the divergence of the Reynolds Stress Tensor (RST) through a Neural Network (NN). This choice is driven by the presence of the divergence of RST in the RANS equations. Furthermore, once this data-driven approach is trained, there is no need to run any turbulence model to close the equations. Finally, it is well known that a good approximation of a function it is not necessarily a good approximation of its derivative. The architecture and inputs choices of the proposed network guarantee both Galilean and coordinates-frame rotation invariances by looking to a vector basis expansion of the divergence of the RST. Two well-known test cases are used to show advantages of the proposed method compared to classic turbulence models.

Variational Physics Informed Neural Networks: the role of quadratures and test functions

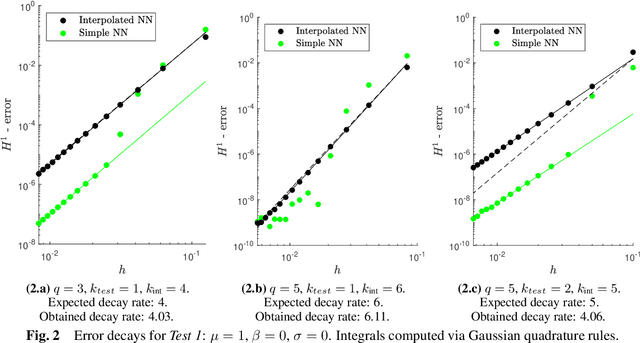
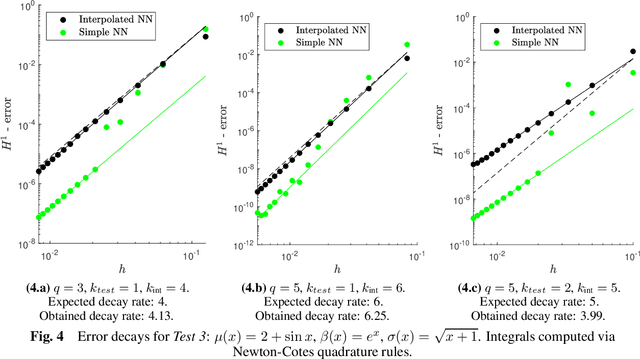
In this work we analyze how Gaussian or Newton-Cotes quadrature rules of different precisions and piecewise polynomial test functions of different degrees affect the convergence rate of Variational Physics Informed Neural Networks (VPINN) with respect to mesh refinement, while solving elliptic boundary-value problems. Using a Petrov-Galerkin framework relying on an inf-sup condition, we derive an a priori error estimate in the energy norm between the exact solution and a suitable high-order piecewise interpolant of a computed neural network. Numerical experiments confirm the theoretical predictions, and also indicate that the error decay follows the same behavior when the neural network is not interpolated. Our results suggest, somehow counterintuitively, that for smooth solutions the best strategy to achieve a high decay rate of the error consists in choosing test functions of the lowest polynomial degree, while using quadrature formulas of suitably high precision.