Parametrized Multi-Agent Routing via Deep Attention Models

We propose a scalable deep learning framework for parametrized sequential decision-making (ParaSDM), where multiple agents jointly optimize discrete action policies and shared continuous parameters. A key subclass of this setting arises in Facility-Location and Path Optimization (FLPO), where multi-agent systems must simultaneously determine optimal routes and facility locations, aiming to minimize the cumulative transportation cost within the network. FLPO problems are NP-hard due to their mixed discrete-continuous structure and highly non-convex objective. To address this, we integrate the Maximum Entropy Principle (MEP) with a neural policy model called the Shortest Path Network (SPN)-a permutation-invariant encoder-decoder that approximates the MEP solution while enabling efficient gradient-based optimization over shared parameters. The SPN achieves up to 100$\times$ speedup in policy inference and gradient computation compared to MEP baselines, with an average optimality gap of approximately 6% across a wide range of problem sizes. Our FLPO approach yields over 10$\times$ lower cost than metaheuristic baselines while running significantly faster, and matches Gurobi's optimal cost with annealing at a 1500$\times$ speedup-establishing a new state of the art for ParaSDM problems. These results highlight the power of structured deep models for solving large-scale mixed-integer optimization tasks.

A Deterministic Annealing Approach to the Multiple Traveling Salesmen and Related Problems

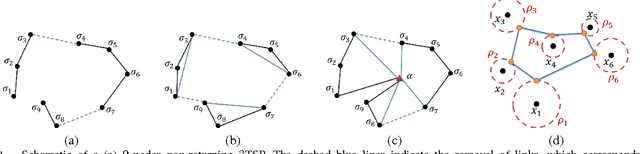
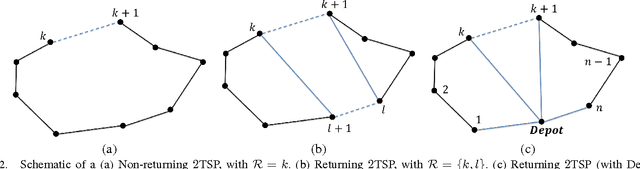
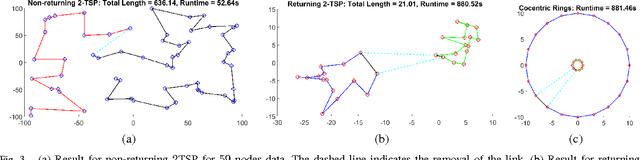
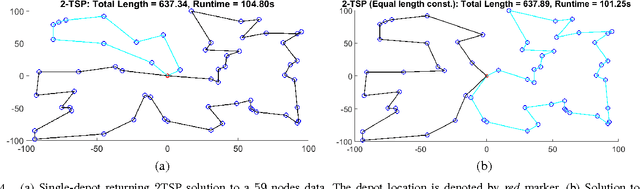
This paper presents a novel and efficient heuristic framework for approximating the solutions to the multiple traveling salesmen problem (m-TSP) and other variants on the TSP. The approach adopted in this paper is an extension of the Maximum-Entropy-Principle (MEP) and the Deterministic Annealing (DA) algorithm. The framework is presented as a general tool that can be suitably adapted to a number of variants on the basic TSP. Additionally, unlike most other heuristics for the TSP, the framework presented in this paper is independent of the edges defined between any two pairs of nodes. This makes the algorithm particularly suited for variants such as the close-enough traveling salesman problem (CETSP) which are challenging due to added computational complexity. The examples presented in this paper illustrate the effectiveness of this new framework for use in TSP and many variants thereof.