Green Tsetlin Redefining Efficiency in Tsetlin Machine Frameworks

Green Tsetlin (GT) is a Tsetlin Machine (TM) framework developed to solve real-world problems using TMs. Several frameworks already exist that provide access to TM implementations. However, these either lack features or have a research-first focus. GT is an easy-to-use framework that aims to lower the complexity and provide a production-ready TM implementation that is great for experienced practitioners and beginners. To this end, GT establishes a clear separation between training and inference. A C++ backend with a Python interface provides competitive training and inference performance, with the option of running in pure Python. It also integrates support for critical components such as exporting trained models, hyper-parameter search, and cross-validation out-of-the-box.

The Sparse Tsetlin Machine: Sparse Representation with Active Literals

This paper introduces the Sparse Tsetlin Machine (STM), a novel Tsetlin Machine (TM) that processes sparse data efficiently. Traditionally, the TM does not consider data characteristics such as sparsity, commonly seen in NLP applications and other bag-of-word-based representations. Consequently, a TM must initialize, store, and process a significant number of zero values, resulting in excessive memory usage and computational time. Previous attempts at creating a sparse TM have predominantly been unsuccessful, primarily due to their inability to identify which literals are sufficient for TM training. By introducing Active Literals (AL), the STM can focus exclusively on literals that actively contribute to the current data representation, significantly decreasing memory footprint and computational time while demonstrating competitive classification performance.

Building Concise Logical Patterns by Constraining Tsetlin Machine Clause Size

Tsetlin machine (TM) is a logic-based machine learning approach with the crucial advantages of being transparent and hardware-friendly. While TMs match or surpass deep learning accuracy for an increasing number of applications, large clause pools tend to produce clauses with many literals (long clauses). As such, they become less interpretable. Further, longer clauses increase the switching activity of the clause logic in hardware, consuming more power. This paper introduces a novel variant of TM learning - Clause Size Constrained TMs (CSC-TMs) - where one can set a soft constraint on the clause size. As soon as a clause includes more literals than the constraint allows, it starts expelling literals. Accordingly, oversized clauses only appear transiently. To evaluate CSC-TM, we conduct classification, clustering, and regression experiments on tabular data, natural language text, images, and board games. Our results show that CSC-TM maintains accuracy with up to 80 times fewer literals. Indeed, the accuracy increases with shorter clauses for TREC, IMDb, and BBC Sports. After the accuracy peaks, it drops gracefully as the clause size approaches a single literal. We finally analyze CSC-TM power consumption and derive new convergence properties.

Coalesced Multi-Output Tsetlin Machines with Clause Sharing

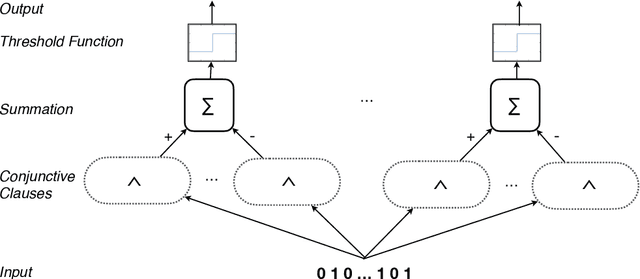
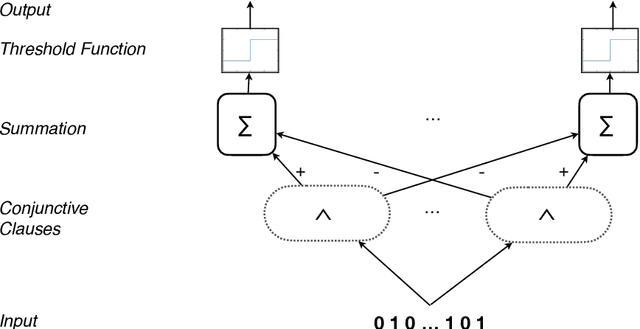
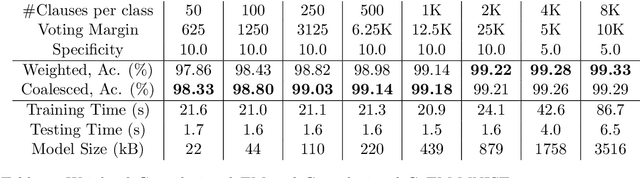
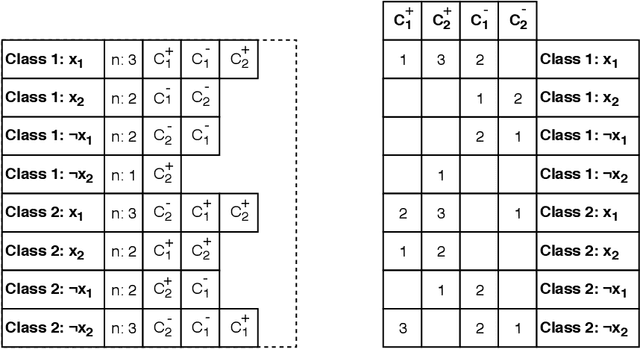
Using finite-state machines to learn patterns, Tsetlin machines (TMs) have obtained competitive accuracy and learning speed across several benchmarks, with frugal memory- and energy footprint. A TM represents patterns as conjunctive clauses in propositional logic (AND-rules), each clause voting for or against a particular output. While efficient for single-output problems, one needs a separate TM per output for multi-output problems. Employing multiple TMs hinders pattern reuse because each TM then operates in a silo. In this paper, we introduce clause sharing, merging multiple TMs into a single one. Each clause is related to each output by using a weight. A positive weight makes the clause vote for output $1$, while a negative weight makes the clause vote for output $0$. The clauses thus coalesce to produce multiple outputs. The resulting coalesced Tsetlin Machine (CoTM) simultaneously learns both the weights and the composition of each clause by employing interacting Stochastic Searching on the Line (SSL) and Tsetlin Automata (TA) teams. Our empirical results on MNIST, Fashion-MNIST, and Kuzushiji-MNIST show that CoTM obtains significantly higher accuracy than TM on $50$- to $1$K-clause configurations, indicating an ability to repurpose clauses. E.g., accuracy goes from $71.99$% to $89.66$% on Fashion-MNIST when employing $50$ clauses per class (22 Kb memory). While TM and CoTM accuracy is similar when using more than $1$K clauses per class, CoTM reaches peak accuracy $3\times$ faster on MNIST with $8$K clauses. We further investigate robustness towards imbalanced training data. Our evaluations on imbalanced versions of IMDb- and CIFAR10 data show that CoTM is robust towards high degrees of class imbalance. Being able to share clauses, we believe CoTM will enable new TM application domains that involve multiple outputs, such as learning language models and auto-encoding.

Increasing the Inference and Learning Speed of Tsetlin Machines with Clause Indexing

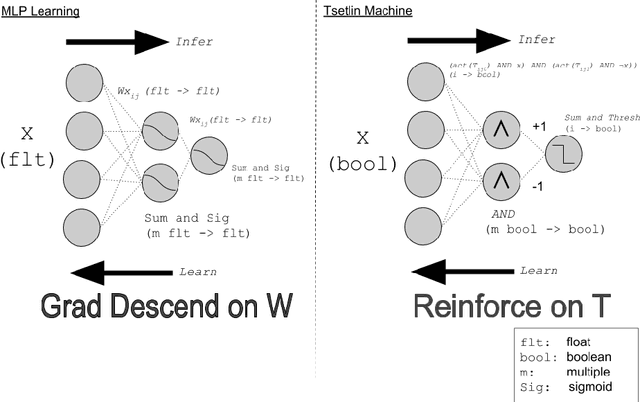
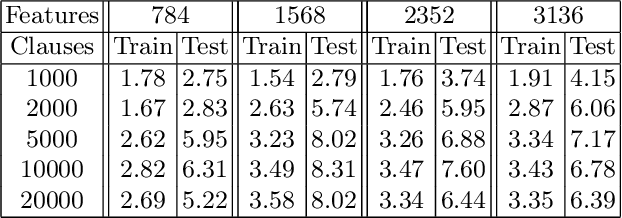
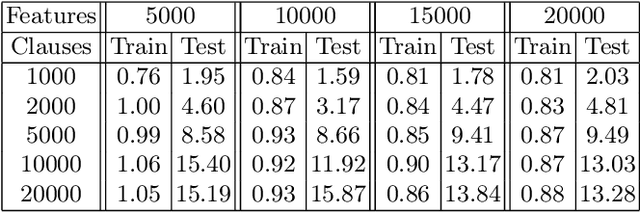
The Tsetlin Machine (TM) is a machine learning algorithm founded on the classical Tsetlin Automaton (TA) and game theory. It further leverages frequent pattern mining and resource allocation principles to extract common patterns in the data, rather than relying on minimizing output error, which is prone to overfitting. Unlike the intertwined nature of pattern representation in neural networks, a TM decomposes problems into self-contained patterns, represented as conjunctive clauses. The clause outputs, in turn, are combined into a classification decision through summation and thresholding, akin to a logistic regression function, however, with binary weights and a unit step output function. In this paper, we exploit this hierarchical structure by introducing a novel algorithm that avoids evaluating the clauses exhaustively. Instead we use a simple look-up table that indexes the clauses on the features that falsify them. In this manner, we can quickly evaluate a large number of clauses through falsification, simply by iterating through the features and using the look-up table to eliminate those clauses that are falsified. The look-up table is further structured so that it facilitates constant time updating, thus supporting use also during learning. We report up to 15 times faster classification and three times faster learning on MNIST and Fashion-MNIST image classification, and IMDb sentiment analysis.

The Convolutional Tsetlin Machine

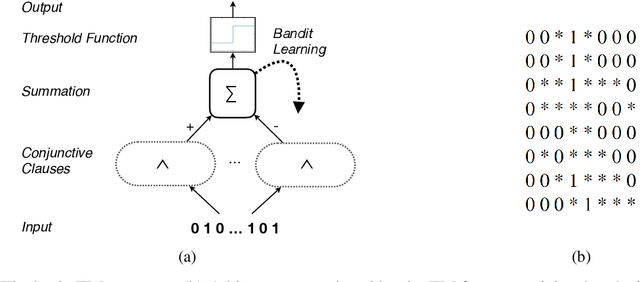
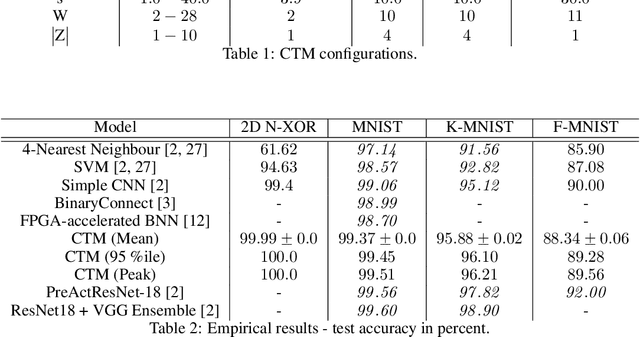
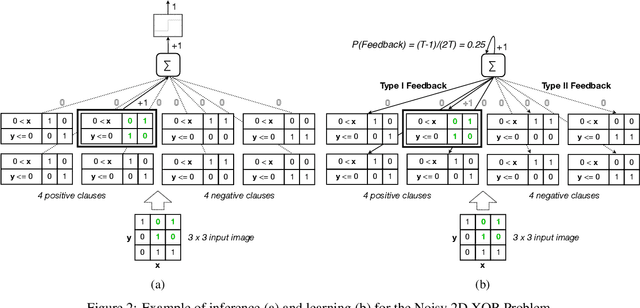
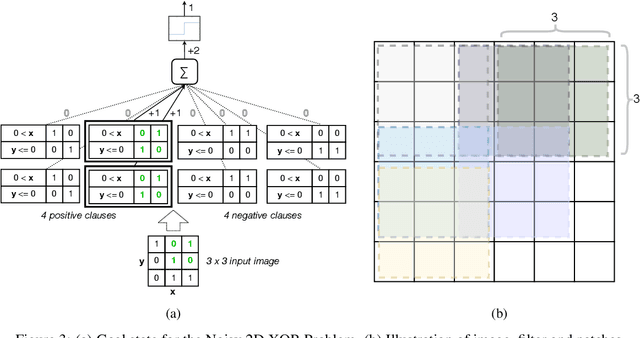
Deep neural networks have obtained astounding successes for important pattern recognition tasks, but they suffer from high computational complexity and the lack of interpretability. The recent Tsetlin Machine (TM) attempts to address this lack by using easy-to-interpret conjunctive clauses in propositional logic to solve complex pattern recognition problems. The TM provides competitive accuracy in several benchmarks, while keeping the important property of interpretability. It further facilitates hardware-near implementation since inputs, patterns, and outputs are expressed as bits, while recognition and learning rely on straightforward bit manipulation. In this paper, we exploit the TM paradigm by introducing the Convolutional Tsetlin Machine (CTM), as an interpretable alternative to convolutional neural networks (CNNs). Whereas the TM categorizes an image by employing each clause once to the whole image, the CTM uses each clause as a convolution filter. That is, a clause is evaluated multiple times, once per image patch taking part in the convolution. To make the clauses location-aware, each patch is further augmented with its coordinates within the image. The output of a convolution clause is obtained simply by ORing the outcome of evaluating the clause on each patch. In the learning phase of the TM, clauses that evaluate to 1 are contrasted against the input. For the CTM, we instead contrast against one of the patches, randomly selected among the patches that made the clause evaluate to 1. Accordingly, the standard Type I and Type II feedback of the classic TM can be employed directly, without further modification. The CTM obtains a peak test accuracy of 99.51% on MNIST, 96.21% on Kuzushiji-MNIST, 89.56% on Fashion-MNIST, and 100.0% on the 2D Noisy XOR Problem, which is competitive with results reported for simple 4-layer CNNs, BinaryConnect, and a recent FPGA-accelerated Binary CNN.

Thompson Sampling Guided Stochastic Searching on the Line for Deceptive Environments with Applications to Root-Finding Problems

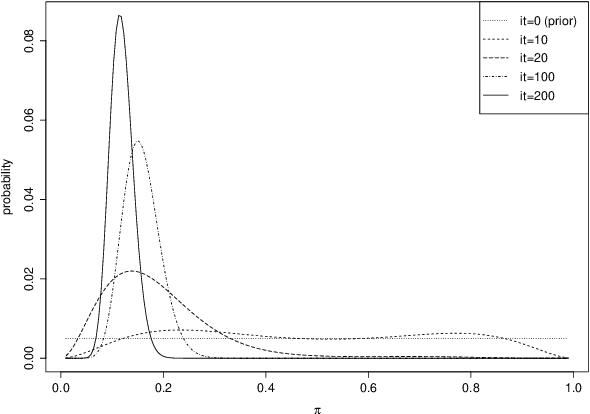
The multi-armed bandit problem forms the foundation for solving a wide range of on-line stochastic optimization problems through a simple, yet effective mechanism. One simply casts the problem as a gambler that repeatedly pulls one out of N slot machine arms, eliciting random rewards. Learning of reward probabilities is then combined with reward maximization, by carefully balancing reward exploration against reward exploitation. In this paper, we address a particularly intriguing variant of the multi-armed bandit problem, referred to as the {\it Stochastic Point Location (SPL) Problem}. The gambler is here only told whether the optimal arm (point) lies to the "left" or to the "right" of the arm pulled, with the feedback being erroneous with probability $1-\pi$. This formulation thus captures optimization in continuous action spaces with both {\it informative} and {\it deceptive} feedback. To tackle this class of problems, we formulate a compact and scalable Bayesian representation of the solution space that simultaneously captures both the location of the optimal arm as well as the probability of receiving correct feedback. We further introduce the accompanying Thompson Sampling guided Stochastic Point Location (TS-SPL) scheme for balancing exploration against exploitation. By learning $\pi$, TS-SPL also supports {\it deceptive} environments that are lying about the direction of the optimal arm. This, in turn, allows us to solve the fundamental Stochastic Root Finding (SRF) Problem. Empirical results demonstrate that our scheme deals with both deceptive and informative environments, significantly outperforming competing algorithms both for SRF and SPL.

An Optimal Bayesian Network Based Solution Scheme for the Constrained Stochastic On-line Equi-Partitioning Problem

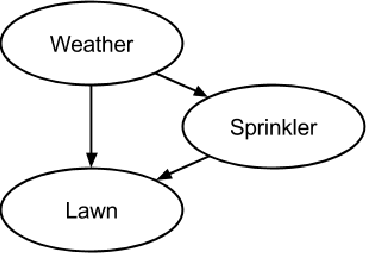
A number of intriguing decision scenarios revolve around partitioning a collection of objects to optimize some application specific objective function. This problem is generally referred to as the Object Partitioning Problem (OPP) and is known to be NP-hard. We here consider a particularly challenging version of OPP, namely, the Stochastic On-line Equi-Partitioning Problem (SO-EPP). In SO-EPP, the target partitioning is unknown and has to be inferred purely from observing an on-line sequence of object pairs. The paired objects belong to the same partition with probability $p$ and to different partitions with probability $1-p$, with $p$ also being unknown. As an additional complication, the partitions are required to be of equal cardinality. Previously, only sub-optimal solution strategies have been proposed for SO- EPP. In this paper, we propose the first optimal solution strategy. In brief, the scheme that we propose, BN-EPP, is founded on a Bayesian network representation of SO-EPP problems. Based on probabilistic reasoning, we are not only able to infer the underlying object partitioning with optimal accuracy. We are also able to simultaneously infer $p$, allowing us to accelerate learning as object pairs arrive. Furthermore, our scheme is the first to support arbitrary constraints on the partitioning (Constrained SO-EPP). Being optimal, BN-EPP provides superior performance compared to existing solution schemes. We additionally introduce Walk-BN-EPP, a novel WalkSAT inspired algorithm for solving large scale BN-EPP problems. Finally, we provide a BN-EPP based solution to the problem of order picking, a representative real-life application of BN-EPP.