Somak Dutta
Ridge partial correlation screening for ultrahigh-dimensional data
Apr 27, 2025Abstract:Variable selection in ultrahigh-dimensional linear regression is challenging due to its high computational cost. Therefore, a screening step is usually conducted before variable selection to significantly reduce the dimension. Here we propose a novel and simple screening method based on ordering the absolute sample ridge partial correlations. The proposed method takes into account not only the ridge regularized estimates of the regression coefficients but also the ridge regularized partial variances of the predictor variables providing sure screening property without strong assumptions on the marginal correlations. Simulation study and a real data analysis show that the proposed method has a competitive performance compared with the existing screening procedures. A publicly available software implementing the proposed screening accompanies the article.
Exploratory Factor Analysis of Data on a Sphere
Nov 09, 2021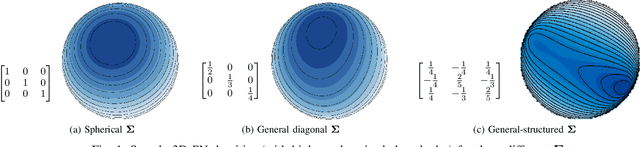
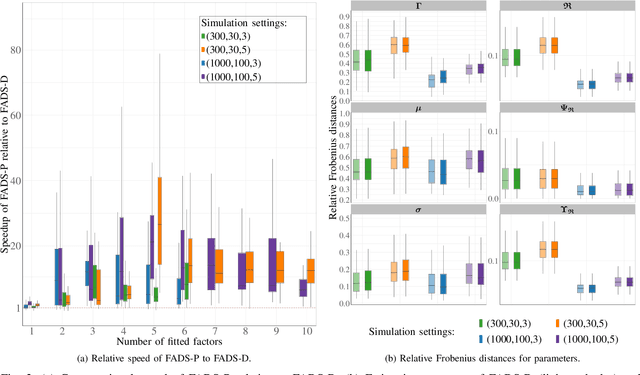
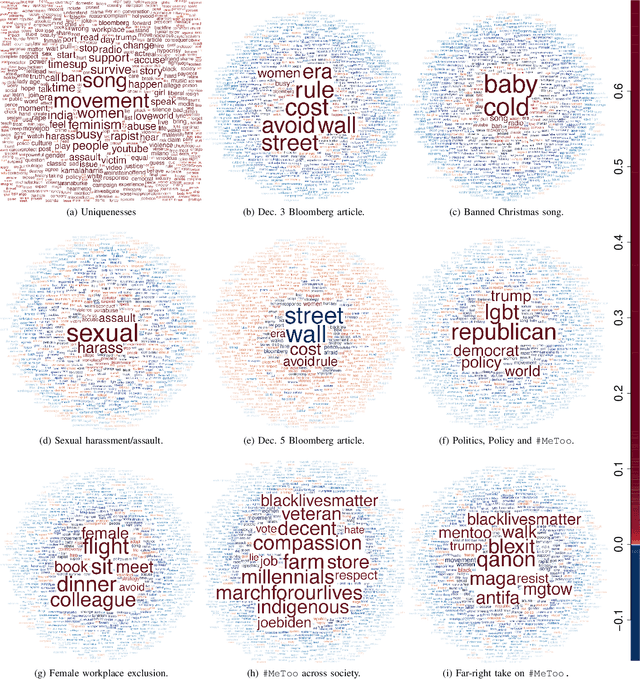
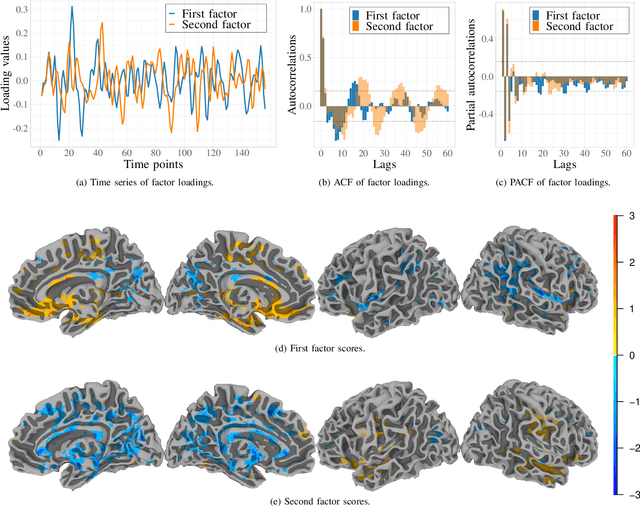
Abstract:Data on high-dimensional spheres arise frequently in many disciplines either naturally or as a consequence of preliminary processing and can have intricate dependence structure that needs to be understood. We develop exploratory factor analysis of the projected normal distribution to explain the variability in such data using a few easily interpreted latent factors. Our methodology provides maximum likelihood estimates through a novel fast alternating expectation profile conditional maximization algorithm. Results on simulation experiments on a wide range of settings are uniformly excellent. Our methodology provides interpretable and insightful results when applied to tweets with the $\#MeToo$ hashtag in early December 2018, to time-course functional Magnetic Resonance Images of the average pre-teen brain at rest, to characterize handwritten digits, and to gene expression data from cancerous cells in the Cancer Genome Atlas.
A Matrix--free Likelihood Method for Exploratory Factor Analysis of High-dimensional Gaussian Data
Jul 27, 2019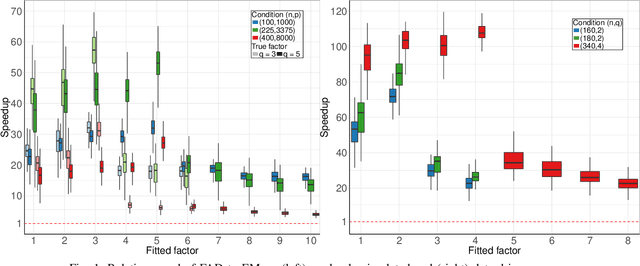
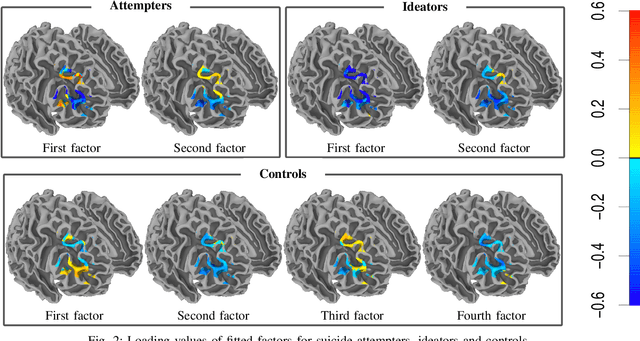
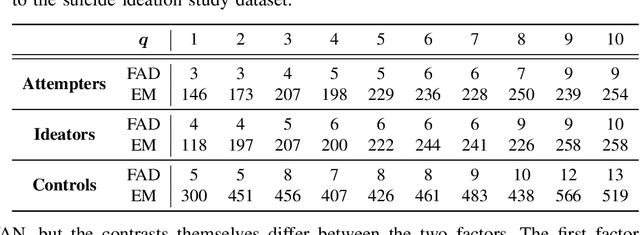
Abstract:This paper proposes a novel profile likelihood method for estimating the covariance parameters in exploratory factor analysis of high-dimensional Gaussian datasets with fewer observations than number of variables. An implicitly restarted Lanczos algorithm and a limited-memory quasi-Newton method are implemented to develop a matrix-free framework for likelihood maximization. Simulation results show that our method is substantially faster than the expectation-maximization solution without sacrificing accuracy. Our method is applied to fit factor models on data from suicide attempters, suicide ideators and a control group.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge