Learning Geometric Invariance for Gait Recognition

The goal of gait recognition is to extract identity-invariant features of an individual under various gait conditions, e.g., cross-view and cross-clothing. Most gait models strive to implicitly learn the common traits across different gait conditions in a data-driven manner to pull different gait conditions closer for recognition. However, relatively few studies have explicitly explored the inherent relations between different gait conditions. For this purpose, we attempt to establish connections among different gait conditions and propose a new perspective to achieve gait recognition: variations in different gait conditions can be approximately viewed as a combination of geometric transformations. In this case, all we need is to determine the types of geometric transformations and achieve geometric invariance, then identity invariance naturally follows. As an initial attempt, we explore three common geometric transformations (i.e., Reflect, Rotate, and Scale) and design a $\mathcal{R}$eflect-$\mathcal{R}$otate-$\mathcal{S}$cale invariance learning framework, named ${\mathcal{RRS}}$-Gait. Specifically, it first flexibly adjusts the convolution kernel based on the specific geometric transformations to achieve approximate feature equivariance. Then these three equivariant-aware features are respectively fed into a global pooling operation for final invariance-aware learning. Extensive experiments on four popular gait datasets (Gait3D, GREW, CCPG, SUSTech1K) show superior performance across various gait conditions.

Blind Orthogonal Least Squares based Compressive Spectrum Sensing

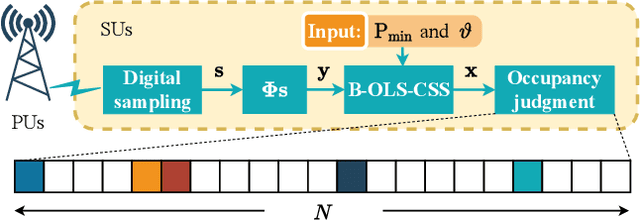
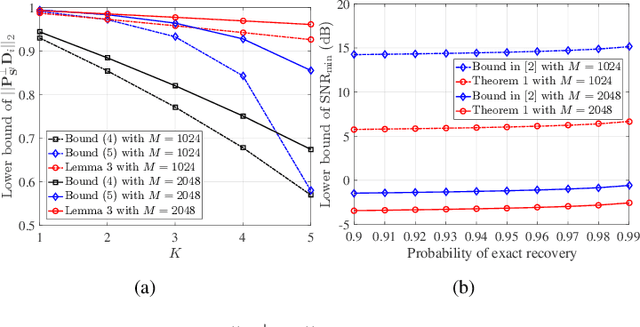
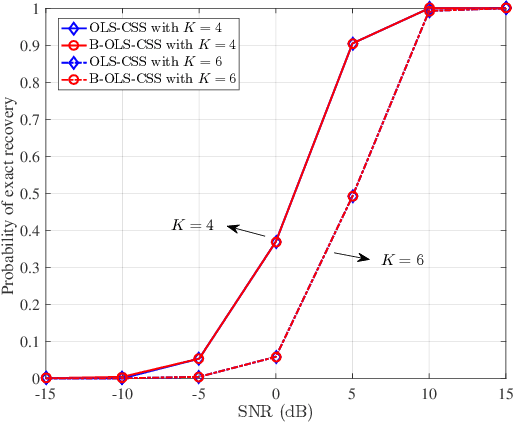
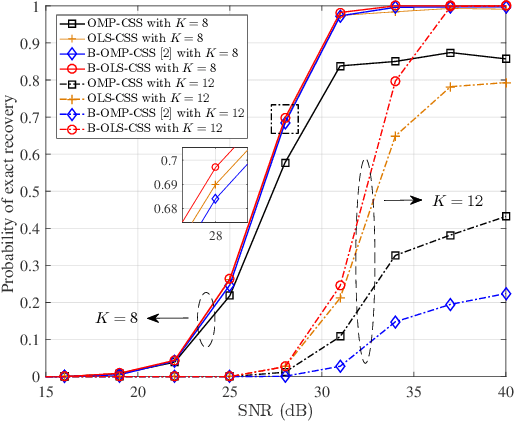
Compressive spectrum sensing (CSS) has been widely studied in wideband cognitive radios, benefiting from the reduction of sampling rate via compressive sensing (CS) technology. However, the sensing performance of most existing CSS excessively relies on the prior information such as spectrum sparsity or noise variance. Thus, a key challenge in practical CSS is how to work effectively even in the absence of such information. In this paper, we propose a blind orthogonal least squares based CSS algorithm (B-OLS-CSS), which functions properly without the requirement of prior information. Specifically, we develop a novel blind stopping rule for the OLS algorithm based on its probabilistic recovery condition. This innovative rule gets rid of the need of the spectrum sparsity or noise information, but only requires the computational-feasible mutual incoherence property of the given measurement matrix. Our theoretical analysis indicates that the signal-to-noise ratio required by the proposed B-OLS-CSS for achieving a certain sensing accuracy is relaxed than that by the benchmark CSS using the OMP algorithm, which is verified by extensive simulation results.