Large Margin Discriminative Loss for Classification

In this paper, we introduce a novel discriminative loss function with large margin in the context of Deep Learning. This loss boosts the discriminative power of neural nets, represented by intra-class compactness and inter-class separability. On the one hand, the class compactness is ensured by close distance of samples of the same class to each other. On the other hand, the inter-class separability is boosted by a margin loss that ensures the minimum distance of each class to its closest boundary. All the terms in our loss have an explicit meaning, giving a direct view of the feature space obtained. We analyze mathematically the relation between compactness and margin term, giving a guideline about the impact of the hyper-parameters on the learned features. Moreover, we also analyze properties of the gradient of the loss with respect to the parameters of the neural net. Based on this, we design a strategy called partial momentum updating that enjoys simultaneously stability and consistency in training. Furthermore, we also investigate generalization errors to have better theoretical insights. Our loss function systematically boosts the test accuracy of models compared to the standard softmax loss in our experiments.

Local convergence of min-max algorithms to differentiable equilibrium on Riemannian manifold

We study min-max algorithms to solve zero-sum differentiable games on Riemannian manifold. The notions of differentiable Stackelberg equilibrium and differentiable Nash equilibrium in Euclidean space are generalized to Riemannian manifold, through an intrinsic definition which does not depend on the choice of local coordinate chart of manifold. We then provide sufficient conditions for the local convergence of the deterministic simultaneous algorithms $\tau$-GDA and $\tau$-SGA near such equilibrium, using a general methodology based on spectral analysis. These algorithms are extended with stochastic gradients and applied to the training of Wasserstein GAN. The discriminator of GAN is constructed from Lipschitz-continuous functions based on Stiefel manifold. We show numerically how the insights obtained from the local convergence analysis may lead to an improvement of GAN models.

Combining Statistical Depth and Fermat Distance for Uncertainty Quantification

We measure the Out-of-domain uncertainty in the prediction of Neural Networks using a statistical notion called ``Lens Depth'' (LD) combined with Fermat Distance, which is able to capture precisely the ``depth'' of a point with respect to a distribution in feature space, without any assumption about the form of distribution. Our method has no trainable parameter. The method is applicable to any classification model as it is applied directly in feature space at test time and does not intervene in training process. As such, it does not impact the performance of the original model. The proposed method gives excellent qualitative result on toy datasets and can give competitive or better uncertainty estimation on standard deep learning datasets compared to strong baseline methods.

Generalized Rectifier Wavelet Covariance Models For Texture Synthesis

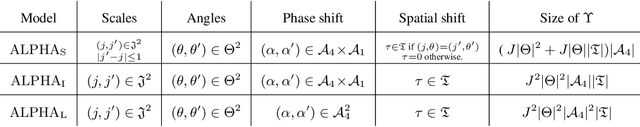
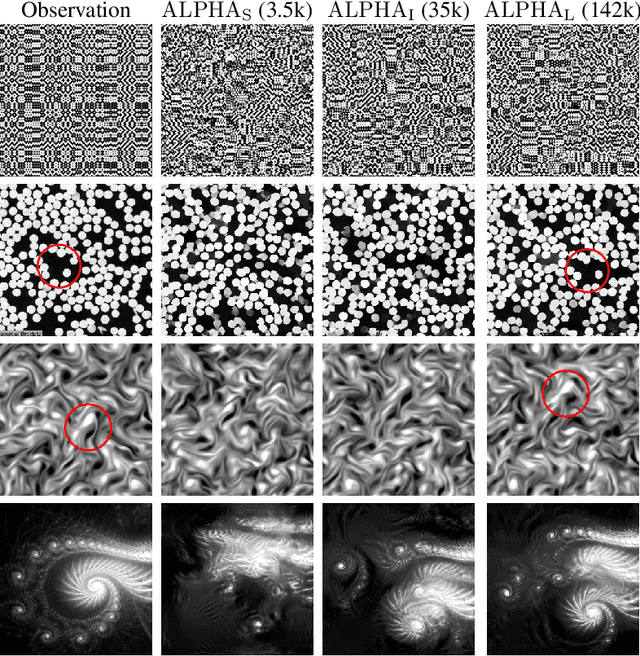
State-of-the-art maximum entropy models for texture synthesis are built from statistics relying on image representations defined by convolutional neural networks (CNN). Such representations capture rich structures in texture images, outperforming wavelet-based representations in this regard. However, conversely to neural networks, wavelets offer meaningful representations, as they are known to detect structures at multiple scales (e.g. edges) in images. In this work, we propose a family of statistics built upon non-linear wavelet based representations, that can be viewed as a particular instance of a one-layer CNN, using a generalized rectifier non-linearity. These statistics significantly improve the visual quality of previous classical wavelet-based models, and allow one to produce syntheses of similar quality to state-of-the-art models, on both gray-scale and color textures.

On the Nash equilibrium of moment-matching GANs for stationary Gaussian processes

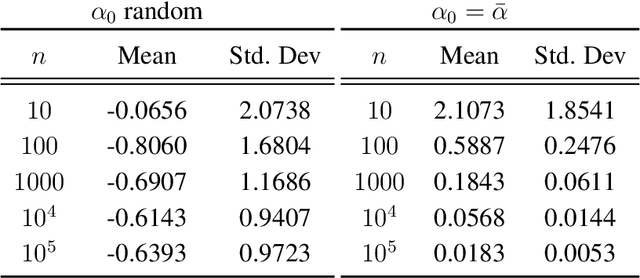
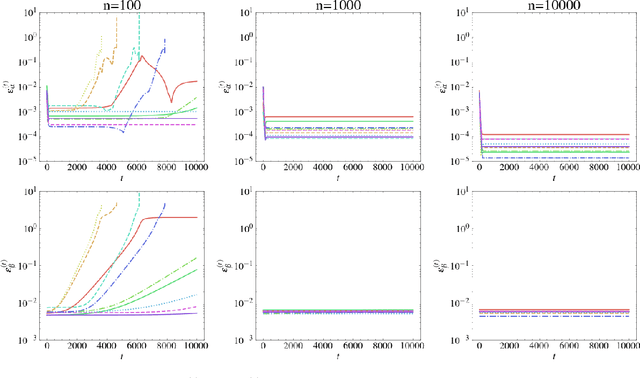
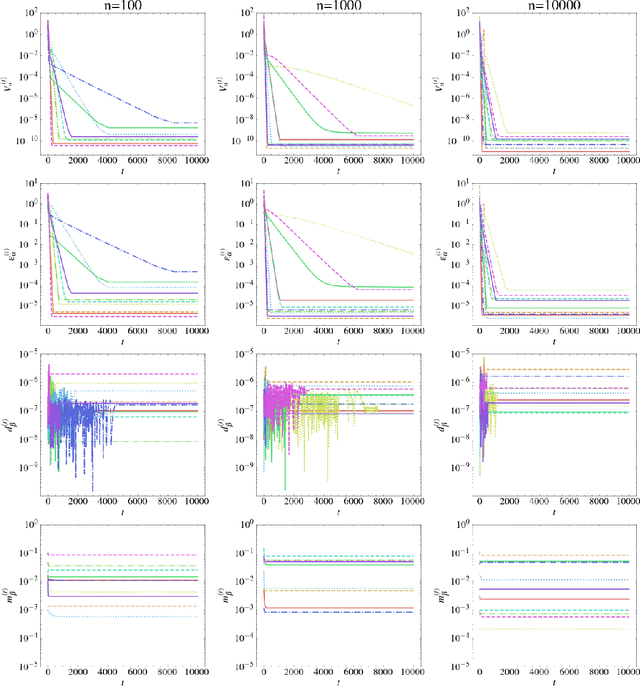
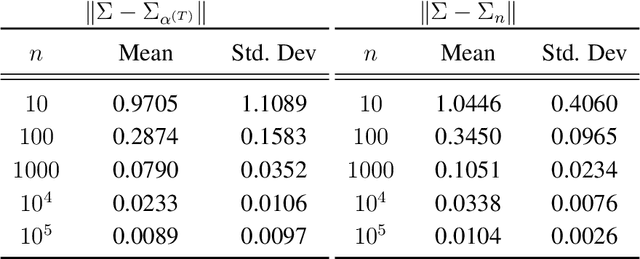
Generative Adversarial Networks (GANs) learn an implicit generative model from data samples through a two-player game. In this paper, we study the existence of Nash equilibrium of the game which is consistent as the number of data samples grows to infinity. In a realizable setting where the goal is to estimate the ground-truth generator of a stationary Gaussian process, we show that the existence of consistent Nash equilibrium depends crucially on the choice of the discriminator family. The discriminator defined from second-order statistical moments can result in non-existence of Nash equilibrium, existence of consistent non-Nash equilibrium, or existence and uniqueness of consistent Nash equilibrium, depending on whether symmetry properties of the generator family are respected. We further study the local stability and global convergence of gradient descent-ascent methods towards consistent equilibrium.

On the Relationships between Transform-Learning NMF and Joint-Diagonalization

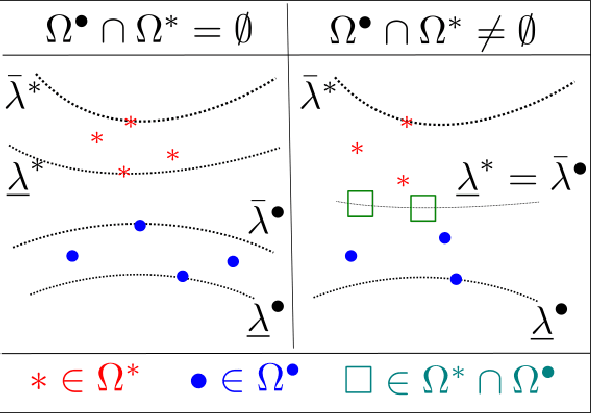
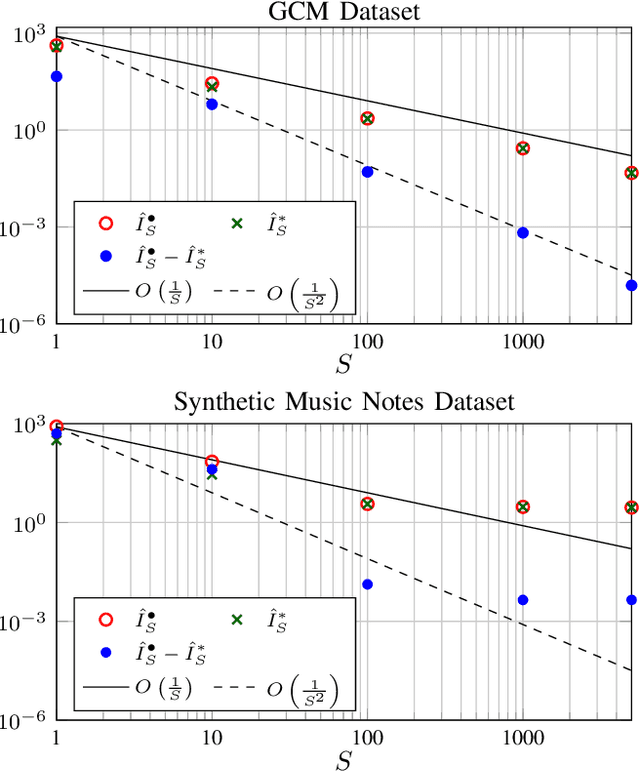
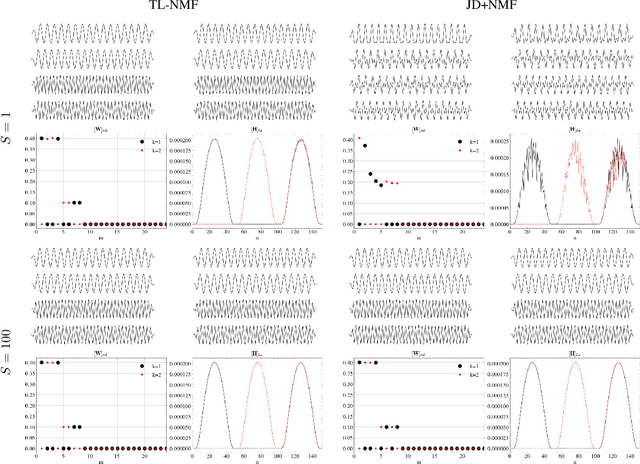
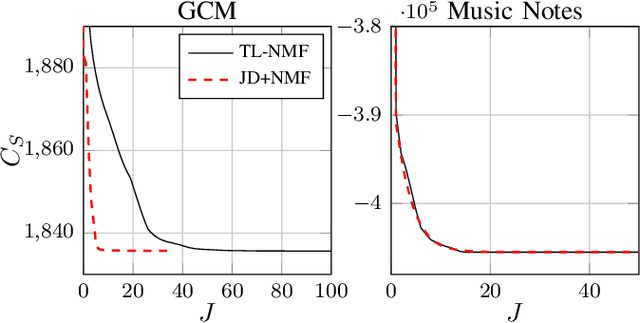
Non-negative matrix factorization with transform learning (TL-NMF) is a recent idea that aims at learning data representations suited to NMF. In this work, we relate TL-NMF to the classical matrix joint-diagonalization (JD) problem. We show that, when the number of data realizations is sufficiently large, TL-NMF can be replaced by a two-step approach -- termed as JD+NMF -- that estimates the transform through JD, prior to NMF computation. In contrast, we found that when the number of data realizations is limited, not only is JD+NMF no longer equivalent to TL-NMF, but the inherent low-rank constraint of TL-NMF turns out to be an essential ingredient to learn meaningful transforms for NMF.

Particle gradient descent model for point process generation

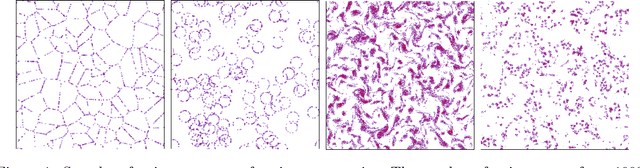
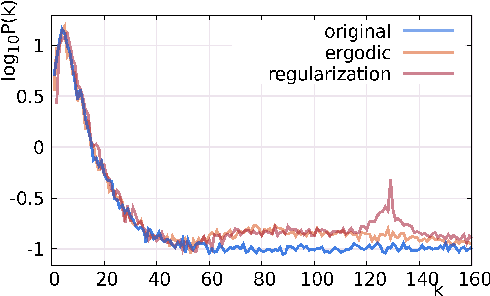
This paper introduces a generative model for planar point processes in a square window, built upon a single realization of a stationary, ergodic point process observed in this window. Inspired by recent advances in gradient descent methods for maximum entropy models, we propose a method to generate similar point patterns by jointly moving particles of an initial Poisson configuration towards a target counting measure. The target measure is generated via a deterministic gradient descent algorithm, so as to match a set of statistics of the given, observed realization. Our statistics are estimators of the multi-scale wavelet phase harmonic covariance, recently proposed in image modeling. They allow one to capture geometric structures through multi-scale interactions between wavelet coefficients. Both our statistics and the gradient descent algorithm scale better with the number of observed points than the classical k-nearest neighbour distances previously used in generative models for point processes, based on the rejection sampling or simulated-annealing. The overall quality of our model is evaluated on point processes with various geometric structures through spectral and topological data analysis.

Maximum Entropy Models from Phase Harmonic Covariances

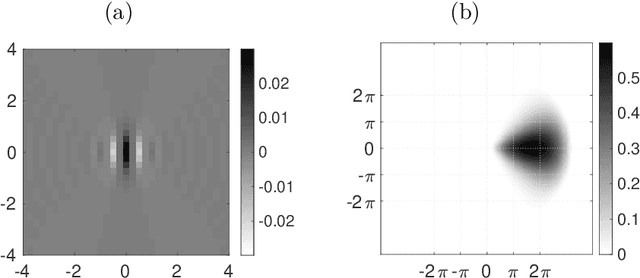
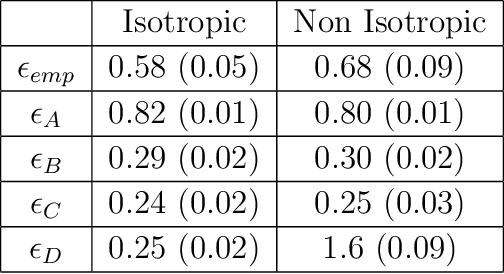
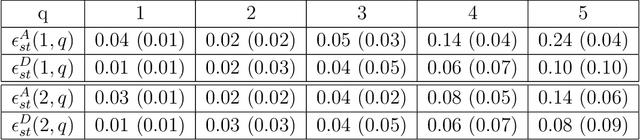
We define maximum entropy models of non-Gaussian stationary random vectors from covariances of non-linear representations. These representations are calculated by multiplying the phase of Fourier or wavelet coefficients with harmonic integers, which amounts to compute a windowed Fourier transform along their phase. Rectifiers in neural networks compute such phase windowing. The covariance of these harmonic coefficients capture dependencies of Fourier and wavelet coefficients across frequencies, by canceling their random phase. We introduce maximum entropy models conditioned by such covariances over a graph of local interactions. These models are approximated by transporting an initial maximum entropy measure with a gradient descent. The precision of wavelet phase harmonic models is numerically evaluated over turbulent flows and other non-Gaussian stationary processes.

Statistical learning of geometric characteristics of wireless networks

Motivated by the prediction of cell loads in cellular networks, we formulate the following new, fundamental problem of statistical learning of geometric marks of point processes: An unknown marking function, depending on the geometry of point patterns, produces characteristics (marks) of the points. One aims at learning this function from the examples of marked point patterns in order to predict the marks of new point patterns. To approximate (interpolate) the marking function, in our baseline approach, we build a statistical regression model of the marks with respect some local point distance representation. In a more advanced approach, we use a global data representation via the scattering moments of random measures, which build informative and stable to deformations data representation, already proven useful in image analysis and related application domains. In this case, the regression of the scattering moments of the marked point patterns with respect to the non-marked ones is combined with the numerical solution of the inverse problem, where the marks are recovered from the estimated scattering moments. Considering some simple, generic marks, often appearing in the modeling of wireless networks, such as the shot-noise values, nearest neighbour distance, and some characteristics of the Voronoi cells, we show that the scattering moments can capture similar geometry information as the baseline approach, and can reach even better performance, especially for non-local marking functions. Our results motivate further development of statistical learning tools for stochastic geometry and analysis of wireless networks, in particular to predict cell loads in cellular networks from the locations of base stations and traffic demand.

Phase Harmonics and Correlation Invariants in Convolutional Neural Networks

We prove that linear rectifiers act as phase transformations on complex analytic extensions of convolutional network coefficients. These phase transformations are linearized over a set of phase harmonics, computed with a Fourier transform. The correlation matrix of one-layer convolutional network coefficients is a translation invariant representation, which is used to build statistical models of stationary processes. We prove that it is Lipschitz continuous and that it has a sparse representation over phase harmonics. When network filters are wavelets, phase harmonic correlations provide important information about phase alignments across scales. We demonstrate numerically that large classes of one-dimensional signals and images are precisely reconstructed with a small fraction of phase harmonic correlations.