Algorithms for Nonlinear Mixed-Integer Location Estimation

For three decades, carrier-phase observations have been used to obtain the most accurate location estimates using global navigation satellite systems (GNSS). These estimates are computed by minimizing a nonlinear mixed-integer least-squares problem. Existing algorithms linearize the problem, orthogonally project it to eliminate real variables, and then solve the integer least-square problem. There is now considerable interest in developing similar localization techniques for terrestrial and indoor settings. We show that algorithms that linearize first fail in these settings and we propose several algorithms for computing the estimates. Some of our algorithms are elimination algorithms that start by eliminating the non-linear terms in the constraints; others construct a geometric arrangement that allows us to efficiently enumerate integer solutions (in polynomial time). We focus on simplified localization problems in which the measurements are range (distance) measurements and carrier phase range measurements, with no nuisance parameters. The simplified problem allows us to focus on the core question of untangling the nonlinearity and the integer nature of some parameters. We show using simulations that the new algorithms are effective at close ranges at which the linearize-first approach fails.

Parallel-in-Time Kalman Smoothing Using Orthogonal Transformations

We present a numerically-stable parallel-in-time linear Kalman smoother. The smoother uses a novel highly-parallel QR factorization for a class of structured sparse matrices for state estimation, and an adaptation of the SelInv selective-inversion algorithm to evaluate the covariance matrices of estimated states. Our implementation of the new algorithm, using the Threading Building Blocks (TBB) library, scales well on both Intel and ARM multi-core servers, achieving speedups of up to 47x on 64 cores. The algorithm performs more arithmetic than sequential smoothers; consequently it is 1.8x to 2.5x slower on a single core. The new algorithm is faster and scales better than the parallel Kalman smoother proposed by S\"arkk\"a and Garc\'{\i}a-Fern\'andez in 2021.

A Mixed Integer Least-Squares Formulation of the GNSS Snapshot Positioning Problem

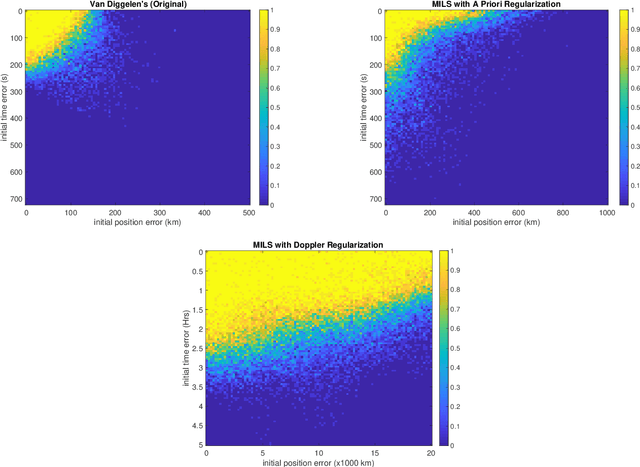
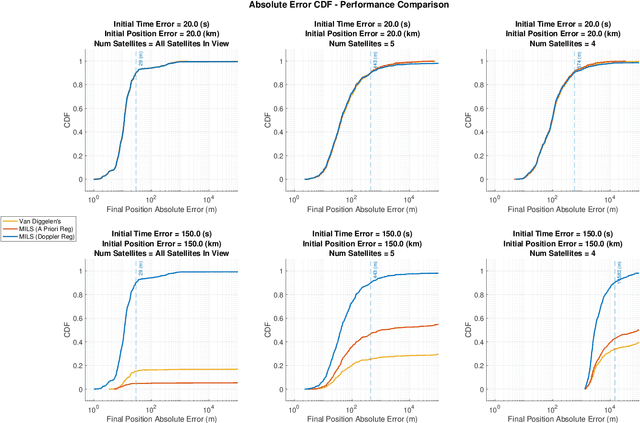
This paper presents a formulation of Snapshot Positioning as a mixed-integer least-squares problem. In snapshot positioning one estimates a position from code-phase and possibly Doppler observations of a Global Navigation Satellite Systems (GNSS) without knowing the time of departure (time stamp) of the codes. Solving the problem allows a receiver to determine a fix from short radio-frequency snapshots missing the time-stamp information embedded in the GNSS data stream. This is used to reduced the time to first fix in some receivers, and it is used in certain wildlife trackers. This paper presents two new formulations of the problem and an algorithm that solves the resulting mixed-integer least-squares problems. We also show that the new formulations can produce fixes even with huge initial errors, much larger than permitted in Van Diggelen's widely-cited coarse-time navigation method.