Algorithms for Nonlinear Mixed-Integer Location Estimation

For three decades, carrier-phase observations have been used to obtain the most accurate location estimates using global navigation satellite systems (GNSS). These estimates are computed by minimizing a nonlinear mixed-integer least-squares problem. Existing algorithms linearize the problem, orthogonally project it to eliminate real variables, and then solve the integer least-square problem. There is now considerable interest in developing similar localization techniques for terrestrial and indoor settings. We show that algorithms that linearize first fail in these settings and we propose several algorithms for computing the estimates. Some of our algorithms are elimination algorithms that start by eliminating the non-linear terms in the constraints; others construct a geometric arrangement that allows us to efficiently enumerate integer solutions (in polynomial time). We focus on simplified localization problems in which the measurements are range (distance) measurements and carrier phase range measurements, with no nuisance parameters. The simplified problem allows us to focus on the core question of untangling the nonlinearity and the integer nature of some parameters. We show using simulations that the new algorithms are effective at close ranges at which the linearize-first approach fails.

Optimized Synthesis of Snapping Fixtures

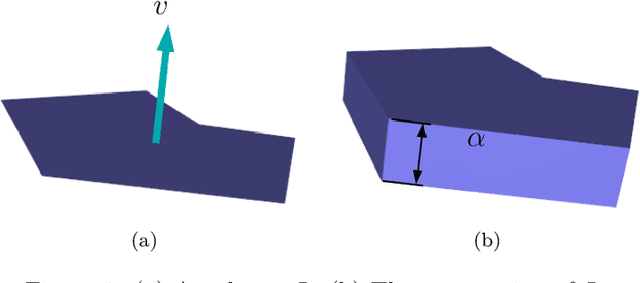
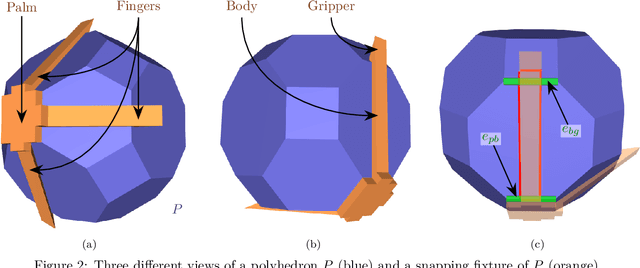
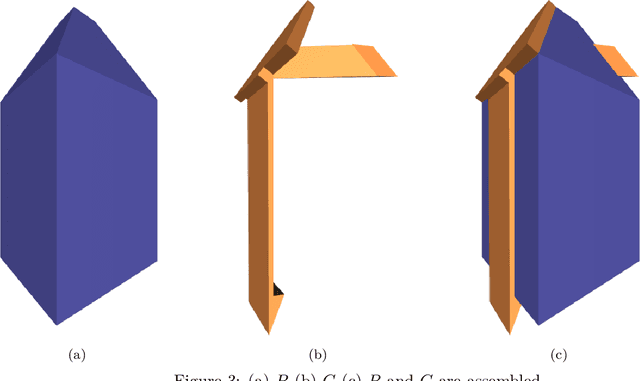
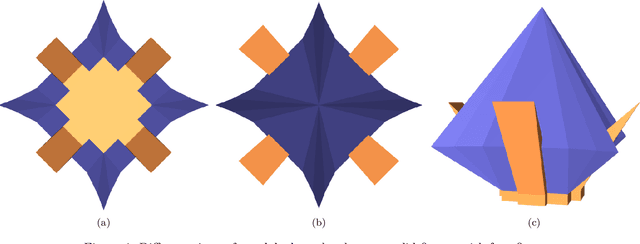
This paper deals with the following separability problem in 3D space: Given a rigid polyhedron $P$ with $n$ vertices, does a semi-rigid polyhedron $G$ exist, such that both polyhedra can be transformed into an inseparable assembled state, where the fixture snaps on to $P$, by applying a linear force and exploiting the mild flexibility of $G$? If such a flexible snapping polyhedron exists, devise an efficient and robust algorithm that constructs it. In simple words, we are looking for s semi-rigid polyhedron $G$, such that when $P$ and $G$ are separate, we can push $G$ towards $P$, slightly bending $G$ on the way, and obtain a configuration, where $G$ is back in its original shape, and both $P$ and $G$ are inseparable as rigid bodies. We define certain properties such a pair of polyhedron and its snapping fixture may possess, and prove two theorems related to the pair. We introduce an algorithm that produces a snapping fixture with such properties in $O(n^5)$ time, if a snapping fixture exists, and an efficient and robust implementation of this algorithm.