NormXLogit: The Head-on-Top Never Lies

The Transformer architecture has emerged as the dominant choice for building large language models (LLMs). However, with new LLMs emerging on a frequent basis, it is important to consider the potential value of architecture-agnostic approaches that can provide interpretability across a variety of architectures. Despite recent successes in the interpretability of LLMs, many existing approaches rely on complex methods that are often tied to a specific model design and come with a significant computational cost. To address these limitations, we propose a novel technique, called NormXLogit, for assessing the significance of individual input tokens. This method operates based on the input and output representations associated with each token. First, we demonstrate that during the pre-training of LLMs, the norms of word embeddings capture the importance of input tokens. Second, we reveal a significant relationship between a token's importance and the extent to which its representation can resemble the model's final prediction. Through extensive analysis, we show that our approach consistently outperforms existing gradient-based methods in terms of faithfulness. Additionally, our method achieves better performance in layer-wise explanations compared to the most prominent architecture-specific methods.

RepMatch: Quantifying Cross-Instance Similarities in Representation Space

Advances in dataset analysis techniques have enabled more sophisticated approaches to analyzing and characterizing training data instances, often categorizing data based on attributes such as ``difficulty''. In this work, we introduce RepMatch, a novel method that characterizes data through the lens of similarity. RepMatch quantifies the similarity between subsets of training instances by comparing the knowledge encoded in models trained on them, overcoming the limitations of existing analysis methods that focus solely on individual instances and are restricted to within-dataset analysis. Our framework allows for a broader evaluation, enabling similarity comparisons across arbitrary subsets of instances, supporting both dataset-to-dataset and instance-to-dataset analyses. We validate the effectiveness of RepMatch across multiple NLP tasks, datasets, and models. Through extensive experimentation, we demonstrate that RepMatch can effectively compare datasets, identify more representative subsets of a dataset (that lead to better performance than randomly selected subsets of equivalent size), and uncover heuristics underlying the construction of some challenge datasets.

Low Complexity Classification Approach for Faster-than-Nyquist (FTN) Signalling Detection

Faster-than-Nyquist (FTN) signaling can improve the spectral efficiency (SE); however, at the expense of high computational complexity to remove the introduced intersymbol interference (ISI). Motivated by the recent success of ML in physical layer (PHY) problems, in this paper we investigate the use of ML in reducing the detection complexity of FTN signaling. In particular, we view the FTN signaling detection problem as a classification task, where the received signal is considered as an unlabeled class sample that belongs to a set of all possible classes samples. If we use an off-shelf classifier, then the set of all possible classes samples belongs to an $N$-dimensional space, where $N$ is the transmission block length, which has a huge computational complexity. We propose a low-complexity classifier (LCC) that exploits the ISI structure of FTN signaling to perform the classification task in $N_p \ll N$-dimension space. The proposed LCC consists of two stages: 1) offline pre-classification that constructs the labeled classes samples in the $N_p$-dimensional space and 2) online classification where the detection of the received samples occurs. The proposed LCC is extended to produce soft-outputs as well. Simulation results show the effectiveness of the proposed LCC in balancing performance and complexity.

Deep Learning-based List Sphere Decoding for Faster-than-Nyquist Signaling Detection

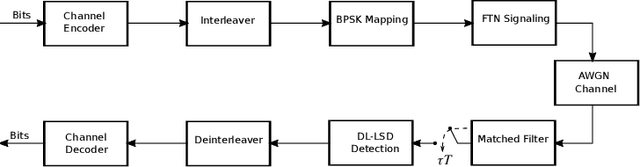
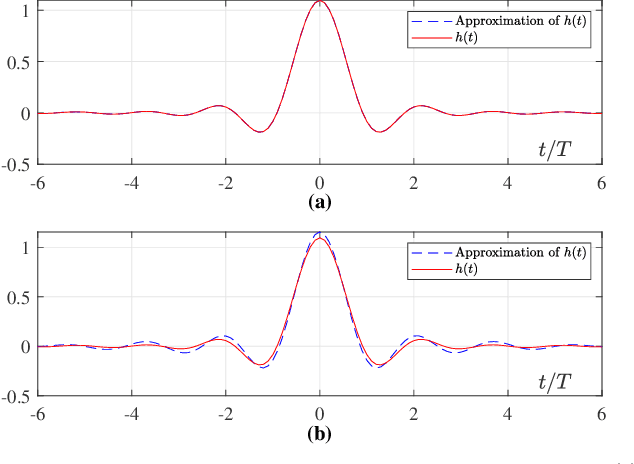
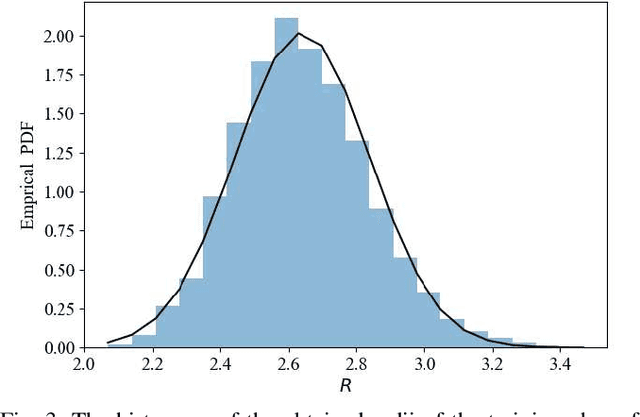
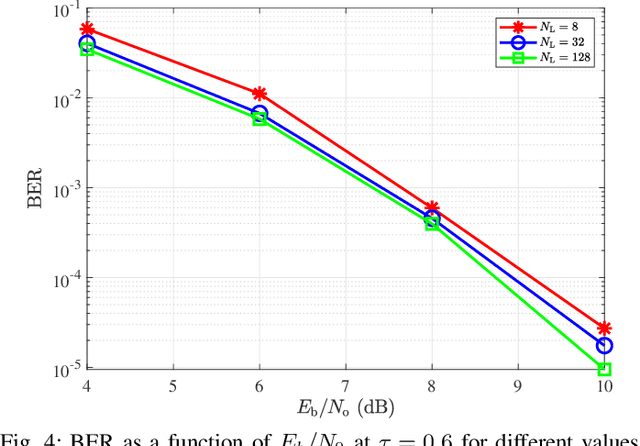
Faster-than-Nyquist (FTN) signaling is a candidate non-orthonormal transmission technique to improve the spectral efficiency (SE) of future communication systems. However, such improvements of the SE are at the cost of additional computational complexity to remove the intentionally introduced intersymbol interference. In this paper, we investigate the use of deep learning (DL) to reduce the detection complexity of FTN signaling. To eliminate the need of having a noise whitening filter at the receiver, we first present an equivalent FTN signaling model based on using a set of orthonormal basis functions and identify its operation region. Second, we propose a DL-based list sphere decoding (DL-LSD) algorithm that selects and updates the initial radius of the original LSD to guarantee a pre-defined number $N_{\text{L}}$ of lattice points inside the hypersphere. This is achieved by training a neural network to output an approximate initial radius that includes $N_{\text{L}}$ lattice points. At the testing phase, if the hypersphere has more than $N_{\text{L}}$ lattice points, we keep the $N_{\text{L}}$ closest points to the point corresponding to the received FTN signal; however, if the hypersphere has less than $N_{\text{L}}$ points, we increase the approximate initial radius by a value that depends on the standard deviation of the distribution of the output radii from the training phase. Then, the approximate value of the log-likelihood ratio (LLR) is calculated based on the obtained $N_{\text{L}}$ points. Simulation results show that the computational complexity of the proposed DL-LSD is lower than its counterpart of the original LSD by orders of magnitude.