Explanations Go Linear: Interpretable and Individual Latent Encoding for Post-hoc Explainability

Post-hoc explainability is essential for understanding black-box machine learning models. Surrogate-based techniques are widely used for local and global model-agnostic explanations but have significant limitations. Local surrogates capture non-linearities but are computationally expensive and sensitive to parameters, while global surrogates are more efficient but struggle with complex local behaviors. In this paper, we present ILLUME, a flexible and interpretable framework grounded in representation learning, that can be integrated with various surrogate models to provide explanations for any black-box classifier. Specifically, our approach combines a globally trained surrogate with instance-specific linear transformations learned with a meta-encoder to generate both local and global explanations. Through extensive empirical evaluations, we demonstrate the effectiveness of ILLUME in producing feature attributions and decision rules that are not only accurate but also robust and faithful to the black-box, thus providing a unified explanation framework that effectively addresses the limitations of traditional surrogate methods.

Disentangled and Self-Explainable Node Representation Learning

Node representations, or embeddings, are low-dimensional vectors that capture node properties, typically learned through unsupervised structural similarity objectives or supervised tasks. While recent efforts have focused on explaining graph model decisions, the interpretability of unsupervised node embeddings remains underexplored. To bridge this gap, we introduce DiSeNE (Disentangled and Self-Explainable Node Embedding), a framework that generates self-explainable embeddings in an unsupervised manner. Our method employs disentangled representation learning to produce dimension-wise interpretable embeddings, where each dimension is aligned with distinct topological structure of the graph. We formalize novel desiderata for disentangled and interpretable embeddings, which drive our new objective functions, optimizing simultaneously for both interpretability and disentanglement. Additionally, we propose several new metrics to evaluate representation quality and human interpretability. Extensive experiments across multiple benchmark datasets demonstrate the effectiveness of our approach.

DINE: Dimensional Interpretability of Node Embeddings

Graphs are ubiquitous due to their flexibility in representing social and technological systems as networks of interacting elements. Graph representation learning methods, such as node embeddings, are powerful approaches to map nodes into a latent vector space, allowing their use for various graph tasks. Despite their success, only few studies have focused on explaining node embeddings locally. Moreover, global explanations of node embeddings remain unexplored, limiting interpretability and debugging potentials. We address this gap by developing human-understandable explanations for dimensions in node embeddings. Towards that, we first develop new metrics that measure the global interpretability of embedding vectors based on the marginal contribution of the embedding dimensions to predicting graph structure. We say that an embedding dimension is more interpretable if it can faithfully map to an understandable sub-structure in the input graph - like community structure. Having observed that standard node embeddings have low interpretability, we then introduce DINE (Dimension-based Interpretable Node Embedding), a novel approach that can retrofit existing node embeddings by making them more interpretable without sacrificing their task performance. We conduct extensive experiments on synthetic and real-world graphs and show that we can simultaneously learn highly interpretable node embeddings with effective performance in link prediction.

Time-varying Graph Representation Learning via Higher-Order Skip-Gram with Negative Sampling

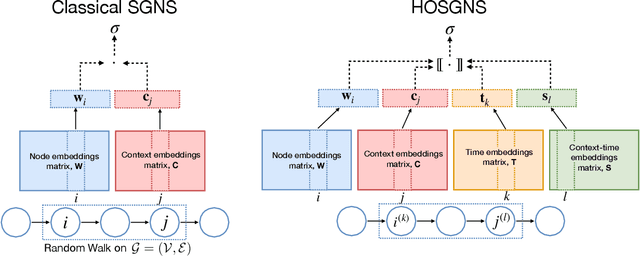
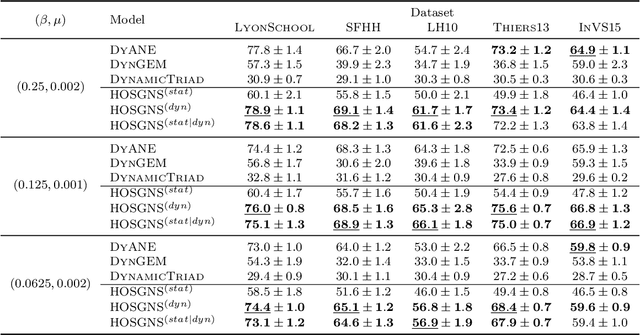
Representation learning models for graphs are a successful family of techniques that project nodes into feature spaces that can be exploited by other machine learning algorithms. Since many real-world networks are inherently dynamic, with interactions among nodes changing over time, these techniques can be defined both for static and for time-varying graphs. Here, we build upon the fact that the skip-gram embedding approach implicitly performs a matrix factorization, and we extend it to perform implicit tensor factorization on different tensor representations of time-varying graphs. We show that higher-order skip-gram with negative sampling (HOSGNS) is able to disentangle the role of nodes and time, with a small fraction of the number of parameters needed by other approaches. We empirically evaluate our approach using time-resolved face-to-face proximity data, showing that the learned time-varying graph representations outperform state-of-the-art methods when used to solve downstream tasks such as network reconstruction, and to predict the outcome of dynamical processes such as disease spreading. The source code and data are publicly available at https://github.com/simonepiaggesi/hosgns.