From Prediction to Action: Critical Role of Performance Estimation for Machine-Learning-Driven Materials Discovery

Materials discovery driven by statistical property models is an iterative decision process, during which an initial data collection is extended with new data proposed by a model-informed acquisition function--with the goal to maximize a certain "reward" over time, such as the maximum property value discovered so far. While the materials science community achieved much progress in developing property models that predict well on average with respect to the training distribution, this form of in-distribution performance measurement is not directly coupled with the discovery reward. This is because an iterative discovery process has a shifting reward distribution that is over-proportionally determined by the model performance for exceptional materials. We demonstrate this problem using the example of bulk modulus maximization among double perovskite oxides. We find that the in-distribution predictive performance suggests random forests as superior to Gaussian process regression, while the results are inverse in terms of the discovery rewards. We argue that the lack of proper performance estimation methods from pre-computed data collections is a fundamental problem for improving data-driven materials discovery, and we propose a novel such estimator that, in contrast to na\"ive reward estimation, successfully predicts Gaussian processes with the "expected improvement" acquisition function as the best out of four options in our demonstrational study for double perovskites. Importantly, it does so without requiring the over thousand ab initio computations that were needed to confirm this prediction.

Better Short than Greedy: Interpretable Models through Optimal Rule Boosting

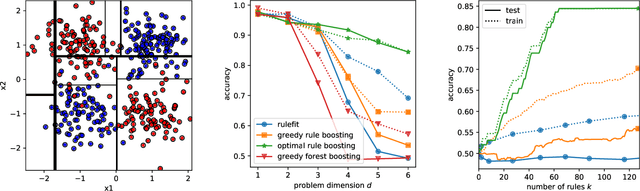
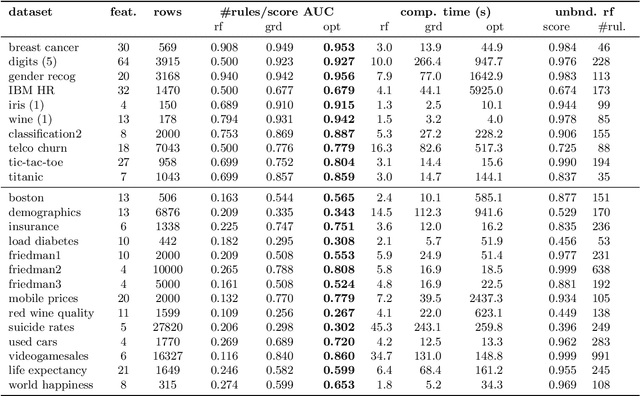
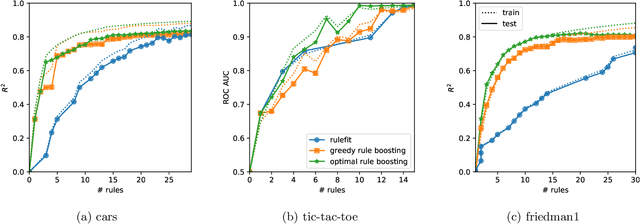
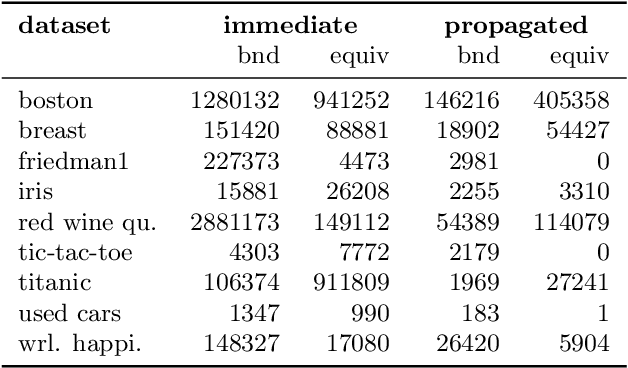
Rule ensembles are designed to provide a useful trade-off between predictive accuracy and model interpretability. However, the myopic and random search components of current rule ensemble methods can compromise this goal: they often need more rules than necessary to reach a certain accuracy level or can even outright fail to accurately model a distribution that can actually be described well with a few rules. Here, we present a novel approach aiming to fit rule ensembles of maximal predictive power for a given ensemble size (and thus model comprehensibility). In particular, we present an efficient branch-and-bound algorithm that optimally solves the per-rule objective function of the popular second-order gradient boosting framework. Our main insight is that the boosting objective can be tightly bounded in linear time of the number of covered data points. Along with an additional novel pruning technique related to rule redundancy, this leads to a computationally feasible approach for boosting optimal rules that, as we demonstrate on a wide range of common benchmark problems, consistently outperforms the predictive performance of boosting greedy rules.