Signal Recovery from Random Dot-Product Graphs Under Local Differential Privacy

We consider the problem of recovering latent information from graphs under $\varepsilon$-edge local differential privacy where the presence of relationships/edges between two users/vertices remains confidential, even from the data curator. For the class of generalized random dot-product graphs, we show that a standard local differential privacy mechanism induces a specific geometric distortion in the latent positions. Leveraging this insight, we show that consistent recovery of the latent positions is achievable by appropriately adjusting the statistical inference procedure for the privatized graph. Furthermore, we prove that our procedure is nearly minimax-optimal under local edge differential privacy constraints. Lastly, we show that this framework allows for consistent recovery of geometric and topological information underlying the latent positions, as encoded in their persistence diagrams. Our results extend previous work from the private community detection literature to a substantially richer class of models and inferential tasks.

Minimax Optimality of Classical Scaling Under General Noise Conditions

We establish the consistency of classical scaling under a broad class of noise models, encompassing many commonly studied cases in literature. Our approach requires only finite fourth moments of the noise, significantly weakening standard assumptions. We derive convergence rates for classical scaling and establish matching minimax lower bounds, demonstrating that classical scaling achieves minimax optimality in recovering the true configuration even when the input dissimilarities are corrupted by noise.

Repelling-Attracting Hamiltonian Monte Carlo

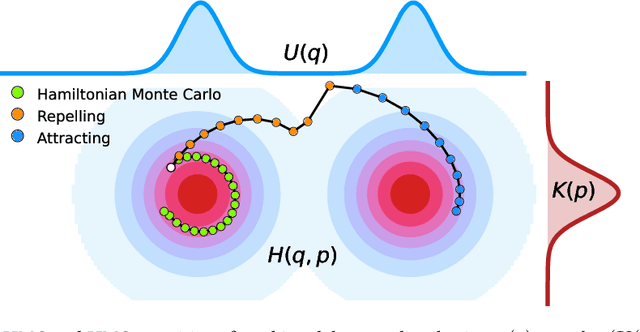
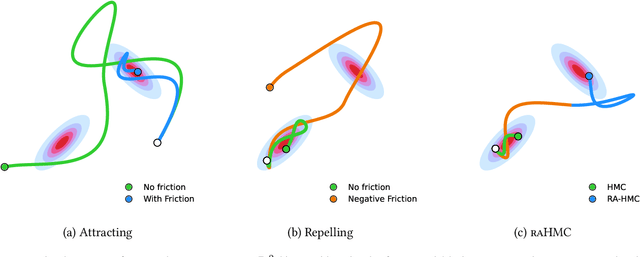
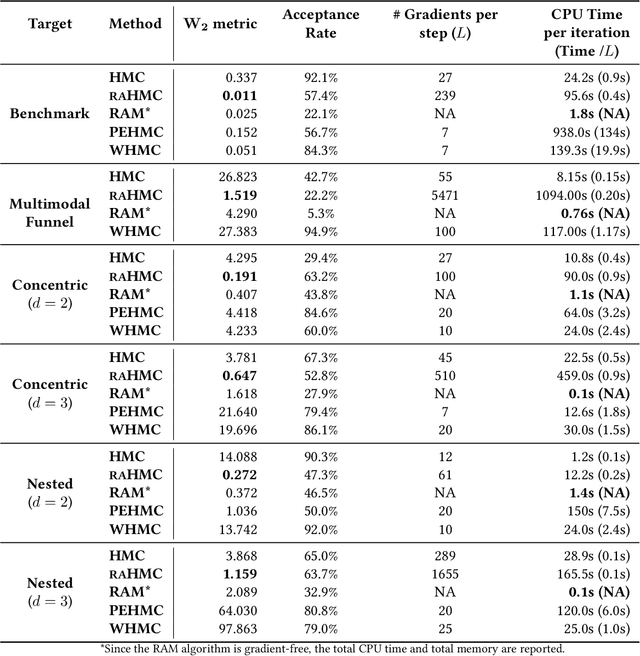
We propose a variant of Hamiltonian Monte Carlo (HMC), called the Repelling-Attracting Hamiltonian Monte Carlo (RAHMC), for sampling from multimodal distributions. The key idea that underpins RAHMC is a departure from the conservative dynamics of Hamiltonian systems, which form the basis of traditional HMC, and turning instead to the dissipative dynamics of conformal Hamiltonian systems. In particular, RAHMC involves two stages: a mode-repelling stage to encourage the sampler to move away from regions of high probability density; and, a mode-attracting stage, which facilitates the sampler to find and settle near alternative modes. We achieve this by introducing just one additional tuning parameter -- the coefficient of friction. The proposed method adapts to the geometry of the target distribution, e.g., modes and density ridges, and can generate proposals that cross low-probability barriers with little to no computational overhead in comparison to traditional HMC. Notably, RAHMC requires no additional information about the target distribution or memory of previously visited modes. We establish the theoretical basis for RAHMC, and we discuss repelling-attracting extensions to several variants of HMC in literature. Finally, we provide a tuning-free implementation via dual-averaging, and we demonstrate its effectiveness in sampling from, both, multimodal and unimodal distributions in high dimensions.

Robust Topological Inference in the Presence of Outliers

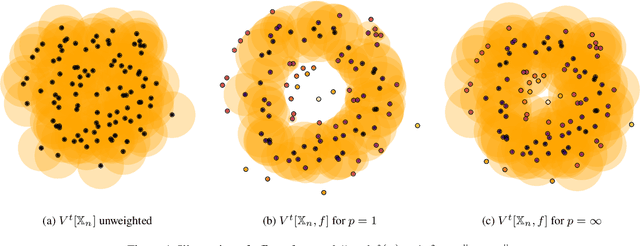
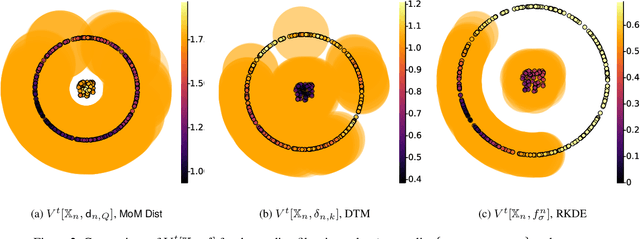
The distance function to a compact set plays a crucial role in the paradigm of topological data analysis. In particular, the sublevel sets of the distance function are used in the computation of persistent homology -- a backbone of the topological data analysis pipeline. Despite its stability to perturbations in the Hausdorff distance, persistent homology is highly sensitive to outliers. In this work, we develop a framework of statistical inference for persistent homology in the presence of outliers. Drawing inspiration from recent developments in robust statistics, we propose a $\textit{median-of-means}$ variant of the distance function ($\textsf{MoM Dist}$), and establish its statistical properties. In particular, we show that, even in the presence of outliers, the sublevel filtrations and weighted filtrations induced by $\textsf{MoM Dist}$ are both consistent estimators of the true underlying population counterpart, and their rates of convergence in the bottleneck metric are controlled by the fraction of outliers in the data. Finally, we demonstrate the advantages of the proposed methodology through simulations and applications.

Robust Persistence Diagrams using Reproducing Kernels

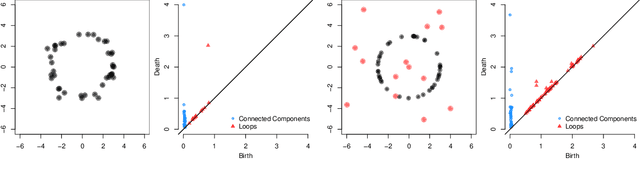
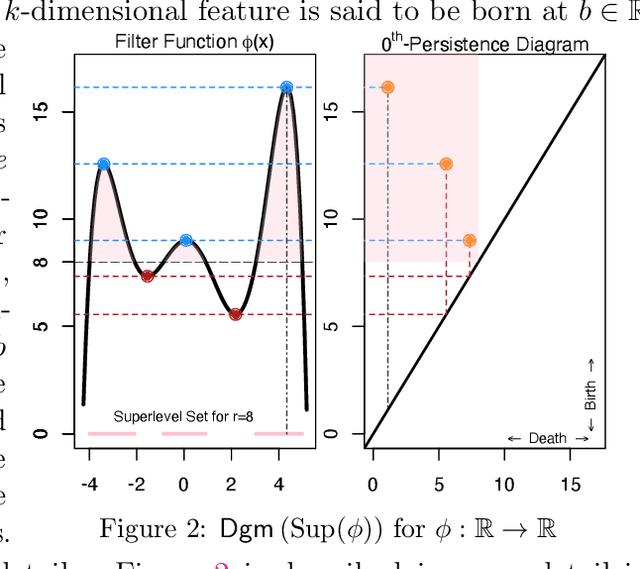
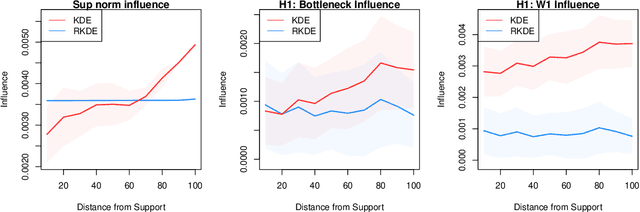
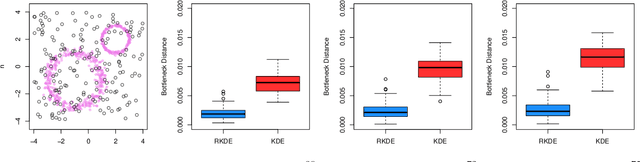
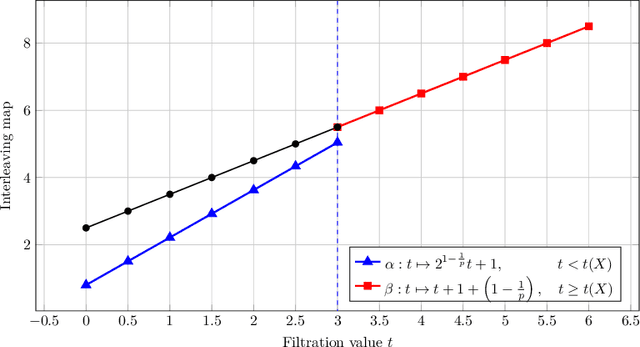
Persistent homology has become an important tool for extracting geometric and topological features from data, whose multi-scale features are summarized in a persistence diagram. From a statistical perspective, however, persistence diagrams are very sensitive to perturbations in the input space. In this work, we develop a framework for constructing robust persistence diagrams from superlevel filtrations of robust density estimators constructed using reproducing kernels. Using an analogue of the influence function on the space of persistence diagrams, we establish the proposed framework to be less sensitive to outliers. The robust persistence diagrams are shown to be consistent estimators in bottleneck distance, with the convergence rate controlled by the smoothness of the kernel. This, in turn, allows us to construct uniform confidence bands in the space of persistence diagrams. Finally, we demonstrate the superiority of the proposed approach on benchmark datasets.