Graph Embedding with Mel-spectrograms for Underwater Acoustic Target Recognition

Underwater acoustic target recognition (UATR) is extremely challenging due to the complexity of ship-radiated noise and the variability of ocean environments. Although deep learning (DL) approaches have achieved promising results, most existing models implicitly assume that underwater acoustic data lie in a Euclidean space. This assumption, however, is unsuitable for the inherently complex topology of underwater acoustic signals, which exhibit non-stationary, non-Gaussian, and nonlinear characteristics. To overcome this limitation, this paper proposes the UATR-GTransformer, a non-Euclidean DL model that integrates Transformer architectures with graph neural networks (GNNs). The model comprises three key components: a Mel patchify block, a GTransformer block, and a classification head. The Mel patchify block partitions the Mel-spectrogram into overlapping patches, while the GTransformer block employs a Transformer Encoder to capture mutual information between split patches to generate Mel-graph embeddings. Subsequently, a GNN enhances these embeddings by modeling local neighborhood relationships, and a feed-forward network (FFN) further performs feature transformation. Experiments results based on two widely used benchmark datasets demonstrate that the UATR-GTransformer achieves performance competitive with state-of-the-art methods. In addition, interpretability analysis reveals that the proposed model effectively extracts rich frequency-domain information, highlighting its potential for applications in ocean engineering.

Application of a Spectral Method to Simulate Quasi-Three-Dimensional Underwater Acoustic Fields

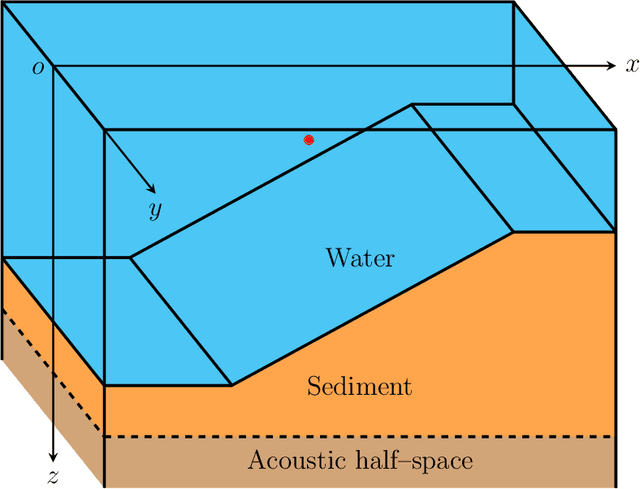
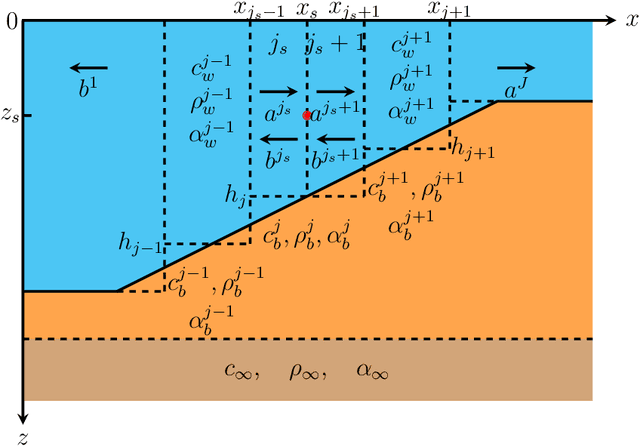
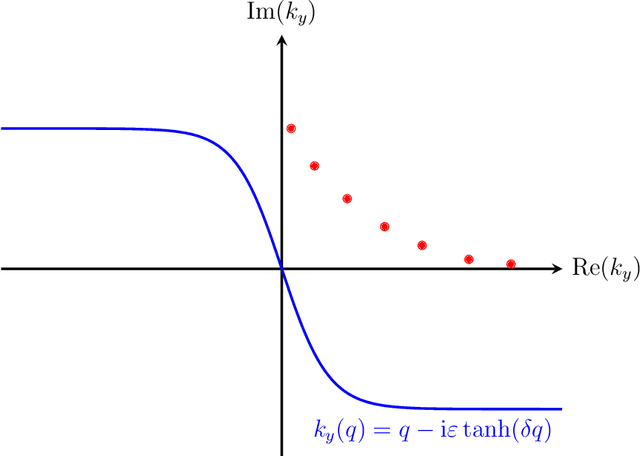
The solution and synthesis of quasi-three-dimensional sound fields have always been core issues in computational ocean acoustics. Traditionally, finite difference algorithms have been employed to solve these problems. In this paper, a novel numerical algorithm based on the spectral method is devised. The quasi-three-dimensional problem is transformed into a problem resembling a two-dimensional line source using an integral transformation strategy. Then, a stair-step approximation is adopted to address the range dependence of the two-dimensional problem; because this approximation is essentially a discretization, the range-dependent two-dimensional problem is further simplified into a one-dimensional problem. Finally, we apply the Chebyshev--Tau spectral method to accurately solve the one-dimensional problem. We present the corresponding numerical program for the proposed algorithm and describe some representative numerical examples. The simulation results ultimately verify the reliability and capability of the proposed algorithm.