Renyi Differential Privacy of Propose-Test-Release and Applications to Private and Robust Machine Learning

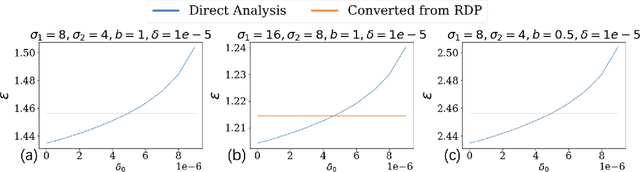
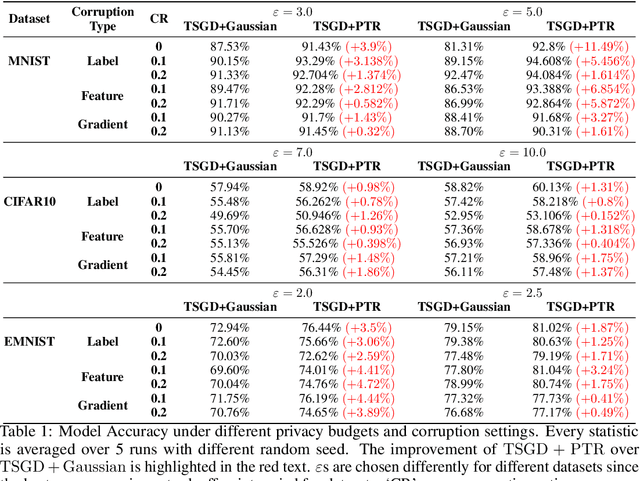
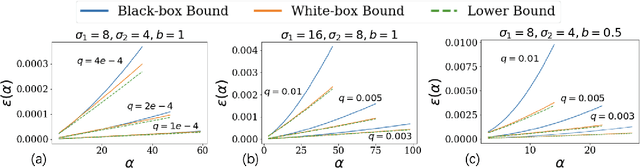
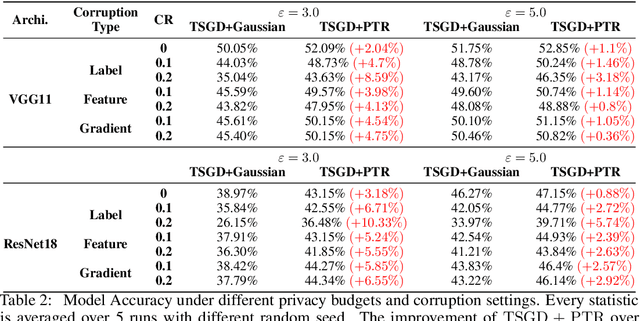
Propose-Test-Release (PTR) is a differential privacy framework that works with local sensitivity of functions, instead of their global sensitivity. This framework is typically used for releasing robust statistics such as median or trimmed mean in a differentially private manner. While PTR is a common framework introduced over a decade ago, using it in applications such as robust SGD where we need many adaptive robust queries is challenging. This is mainly due to the lack of Renyi Differential Privacy (RDP) analysis, an essential ingredient underlying the moments accountant approach for differentially private deep learning. In this work, we generalize the standard PTR and derive the first RDP bound for it when the target function has bounded global sensitivity. We show that our RDP bound for PTR yields tighter DP guarantees than the directly analyzed $(\eps, \delta)$-DP. We also derive the algorithm-specific privacy amplification bound of PTR under subsampling. We show that our bound is much tighter than the general upper bound and close to the lower bound. Our RDP bounds enable tighter privacy loss calculation for the composition of many adaptive runs of PTR. As an application of our analysis, we show that PTR and our theoretical results can be used to design differentially private variants for byzantine robust training algorithms that use robust statistics for gradients aggregation. We conduct experiments on the settings of label, feature, and gradient corruption across different datasets and architectures. We show that PTR-based private and robust training algorithm significantly improves the utility compared with the baseline.

Choosing the Right Algorithm With Hints From Complexity Theory

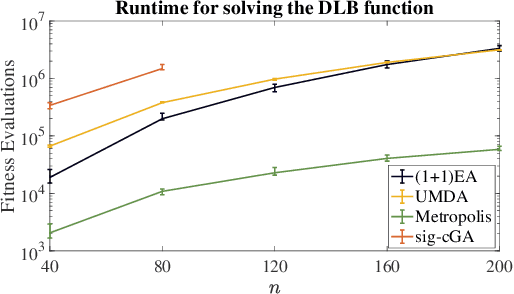
Choosing a suitable algorithm from the myriads of different search heuristics is difficult when faced with a novel optimization problem. In this work, we argue that the purely academic question of what could be the best possible algorithm in a certain broad class of black-box optimizers can give fruitful indications in which direction to search for good established optimization heuristics. We demonstrate this approach on the recently proposed DLB benchmark, for which the only known results are $O(n^3)$ runtimes for several classic evolutionary algorithms and an $O(n^2 \log n)$ runtime for an estimation-of-distribution algorithm. Our finding that the unary unbiased black-box complexity is only $O(n^2)$ suggests the Metropolis algorithm as an interesting candidate and we prove that it solves the DLB problem in quadratic time. Since we also prove that better runtimes cannot be obtained in the class of unary unbiased algorithms, we shift our attention to algorithms that use the information of more parents to generate new solutions. An artificial algorithm of this type having an $O(n \log n)$ runtime leads to the result that the significance-based compact genetic algorithm (sig-cGA) can solve the DLB problem also in time $O(n \log n)$. Our experiments show a remarkably good performance of the Metropolis algorithm, clearly the best of all algorithms regarded for reasonable problem sizes.