Automatic mixed precision for optimizing gained time with constrained loss mean-squared-error based on model partition to sequential sub-graphs

Quantization is essential for Neural Network (NN) compression, reducing model size and computational demands by using lower bit-width data types, though aggressive reduction often hampers accuracy. Mixed Precision (MP) mitigates this tradeoff by varying the numerical precision across network layers. This study focuses on automatically selecting an optimal MP configuration within Post-Training Quantization (PTQ) for inference. The first key contribution is a novel sensitivity metric derived from a first-order Taylor series expansion of the loss function as a function of quantization errors in weights and activations. This metric, based on the Mean Square Error (MSE) of the loss, is efficiently calculated per layer using high-precision forward and backward passes over a small calibration dataset. The metric is additive across layers, with low calibration memory overhead as weight optimization is unnecessary. The second contribution is an accurate hardware-aware method for predicting MP time gain by modeling it as additive for sequential sub-graphs. An algorithm partitions the model graph into sequential subgraphs, measuring time gain for each configuration using a few samples. After calibrating per-layer sensitivity and time gain, an Integer Programming (IP) problem is formulated to maximize time gain while keeping loss MSE below a set threshold. Memory gain and theoretical time gain based on Multiply and Accumulate (MAC) operations are also considered. Rigorous experiments on the Intel Gaudi 2 accelerator validate the approach on several Large Language Models (LLMs).

Feature Whitening via Gradient Transformation for Improved Convergence

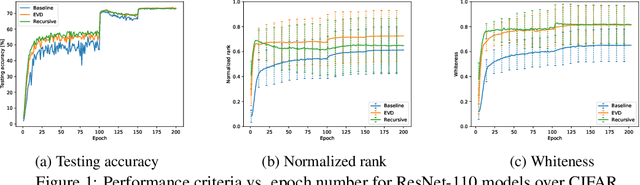
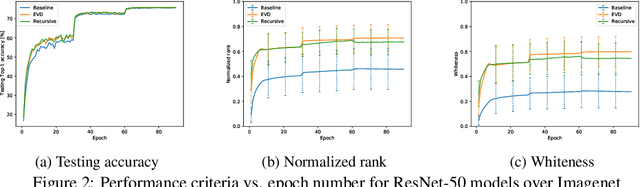
Feature whitening is a known technique for speeding up training of DNN. Under certain assumptions, whitening the activations reduces the Fisher information matrix to a simple identity matrix, in which case stochastic gradient descent is equivalent to the faster natural gradient descent. Due to the additional complexity resulting from transforming the layer inputs and their corresponding gradients in the forward and backward propagation, and from repeatedly computing the Eigenvalue decomposition (EVD), this method is not commonly used to date. In this work, we address the complexity drawbacks of feature whitening. Our contribution is twofold. First, we derive an equivalent method, which replaces the sample transformations by a transformation to the weight gradients, applied to every batch of B samples. The complexity is reduced by a factor of S=(2B), where S denotes the feature dimension of the layer output. As the batch size increases with distributed training, the benefit of using the proposed method becomes more compelling. Second, motivated by the theoretical relation between the condition number of the sample covariance matrix and the convergence speed, we derive an alternative sub-optimal algorithm which recursively reduces the condition number of the latter matrix. Compared to EVD, complexity is reduced by a factor of the input feature dimension M. We exemplify the proposed algorithms with ResNet-based networks for image classification demonstrated on the CIFAR and Imagenet datasets. Parallelizing the proposed algorithms is straightforward and we implement a distributed version thereof. Improved convergence, in terms of speed and attained accuracy, can be observed in our experiments.