Sparse Logistic Regression Learns All Discrete Pairwise Graphical Models

We characterize the effectiveness of a natural and classic algorithm for recovering the Markov graph of a general discrete pairwise graphical model from i.i.d. samples. The algorithm is (appropriately regularized) conditional maximum likelihood, which involves solving a convex program for each node; for Ising models this is $\ell_1$-constrained logistic regression, while for more alphabets an $\ell_{2,1}$ group-norm constraint needs to be used. We show that this algorithm can recover any arbitrary discrete pairwise graphical model, and also characterize its sample complexity as a function of model width, alphabet size, edge parameter accuracy, and the number of variables. We show that along every one of these axes, it matches or improves on all existing results and algorithms for this problem. Our analysis applies a sharp generalization error bound for logistic regression when the weight vector has an $\ell_1$ constraint (or $\ell_{2,1}$ constraint) and the sample vector has an $\ell_{\infty}$ constraint (or $\ell_{2, \infty}$ constraint). We also show that the proposed convex programs can be efficiently optimized in $\tilde{O}(n^2)$ running time (where $n$ is the number of variables) under the same statistical guarantee. Our experimental results verify our analysis.

The Sparse Recovery Autoencoder

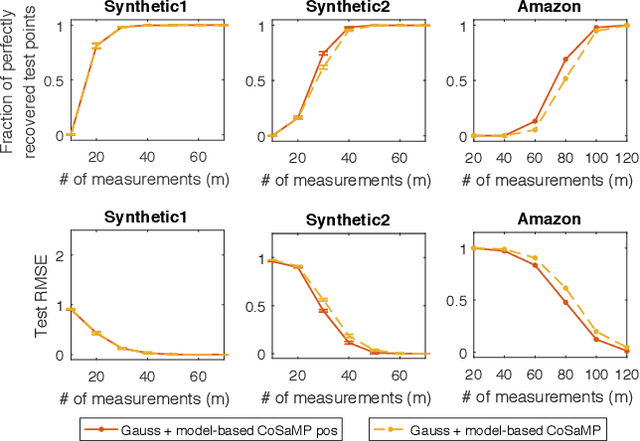
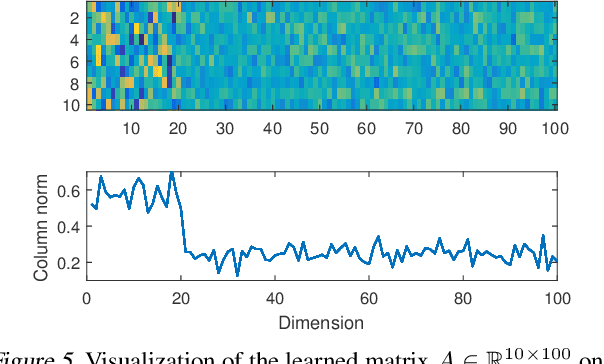
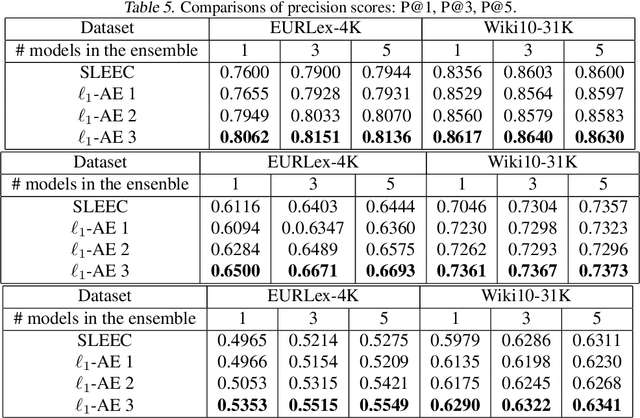
Linear encoding of sparse vectors is widely popular, but is most commonly data-independent -- missing any possible extra (but a-priori unknown) structure beyond sparsity. In this paper we present a new method to learn linear encoders that adapt to data, while still performing well with the widely used $\ell_1$ decoder. The convex $\ell_1$ decoder prevents gradient propagation as needed in standard autoencoder training. Our method is based on the insight that unfolding the convex decoder into $T$ projected gradient steps can address this issue. Our method can be seen as a data-driven way to learn a compressed sensing matrix. Our experiments show that there is indeed additional structure beyond sparsity in several real datasets. Our autoencoder is able to discover it and exploit it to create excellent reconstructions with fewer measurements compared to the previous state of the art methods.

Leveraging Sparsity for Efficient Submodular Data Summarization

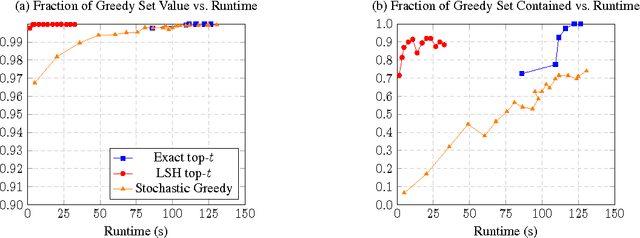
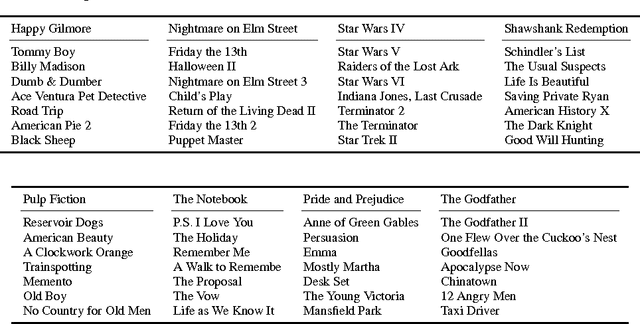
The facility location problem is widely used for summarizing large datasets and has additional applications in sensor placement, image retrieval, and clustering. One difficulty of this problem is that submodular optimization algorithms require the calculation of pairwise benefits for all items in the dataset. This is infeasible for large problems, so recent work proposed to only calculate nearest neighbor benefits. One limitation is that several strong assumptions were invoked to obtain provable approximation guarantees. In this paper we establish that these extra assumptions are not necessary---solving the sparsified problem will be almost optimal under the standard assumptions of the problem. We then analyze a different method of sparsification that is a better model for methods such as Locality Sensitive Hashing to accelerate the nearest neighbor computations and extend the use of the problem to a broader family of similarities. We validate our approach by demonstrating that it rapidly generates interpretable summaries.

Single Pass PCA of Matrix Products

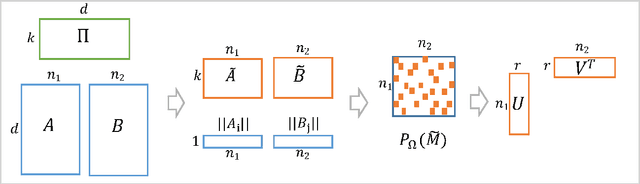
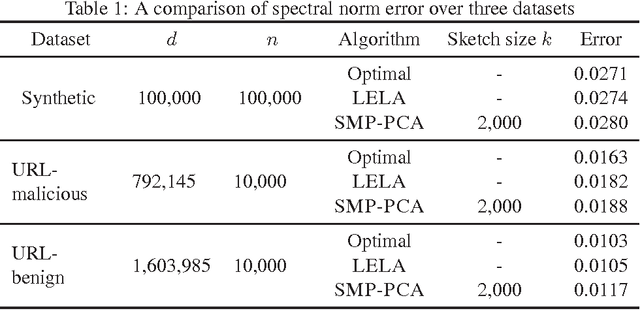
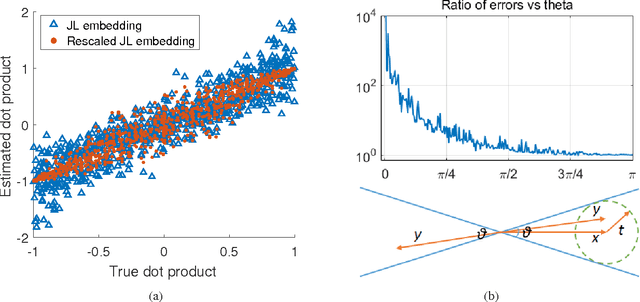
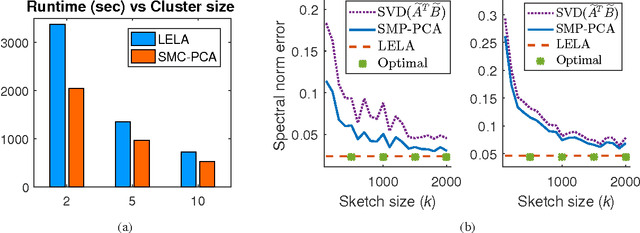
In this paper we present a new algorithm for computing a low rank approximation of the product $A^TB$ by taking only a single pass of the two matrices $A$ and $B$. The straightforward way to do this is to (a) first sketch $A$ and $B$ individually, and then (b) find the top components using PCA on the sketch. Our algorithm in contrast retains additional summary information about $A,B$ (e.g. row and column norms etc.) and uses this additional information to obtain an improved approximation from the sketches. Our main analytical result establishes a comparable spectral norm guarantee to existing two-pass methods; in addition we also provide results from an Apache Spark implementation that shows better computational and statistical performance on real-world and synthetic evaluation datasets.