Shankar Bhamidi
Consistency of Lloyd's Algorithm Under Perturbations
Sep 01, 2023
Abstract:In the context of unsupervised learning, Lloyd's algorithm is one of the most widely used clustering algorithms. It has inspired a plethora of work investigating the correctness of the algorithm under various settings with ground truth clusters. In particular, in 2016, Lu and Zhou have shown that the mis-clustering rate of Lloyd's algorithm on $n$ independent samples from a sub-Gaussian mixture is exponentially bounded after $O(\log(n))$ iterations, assuming proper initialization of the algorithm. However, in many applications, the true samples are unobserved and need to be learned from the data via pre-processing pipelines such as spectral methods on appropriate data matrices. We show that the mis-clustering rate of Lloyd's algorithm on perturbed samples from a sub-Gaussian mixture is also exponentially bounded after $O(\log(n))$ iterations under the assumptions of proper initialization and that the perturbation is small relative to the sub-Gaussian noise. In canonical settings with ground truth clusters, we derive bounds for algorithms such as $k$-means$++$ to find good initializations and thus leading to the correctness of clustering via the main result. We show the implications of the results for pipelines measuring the statistical significance of derived clusters from data such as SigClust. We use these general results to derive implications in providing theoretical guarantees on the misclustering rate for Lloyd's algorithm in a host of applications, including high-dimensional time series, multi-dimensional scaling, and community detection for sparse networks via spectral clustering.
Community detection using low-dimensional network embedding algorithms
Nov 04, 2021
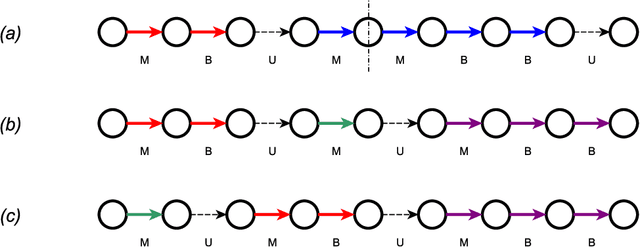
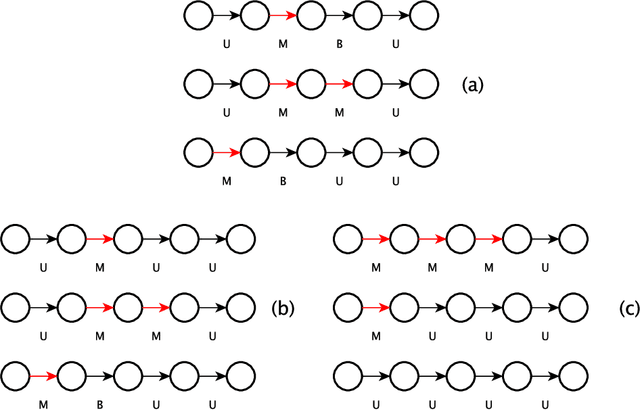
Abstract:With the increasing relevance of large networks in important areas such as the study of contact networks for spread of disease, or social networks for their impact on geopolitics, it has become necessary to study machine learning tools that are scalable to very large networks, often containing millions of nodes. One major class of such scalable algorithms is known as network representation learning or network embedding. These algorithms try to learn representations of network functionals (e.g.~nodes) by first running multiple random walks and then using the number of co-occurrences of each pair of nodes in observed random walk segments to obtain a low-dimensional representation of nodes on some Euclidean space. The aim of this paper is to rigorously understand the performance of two major algorithms, DeepWalk and node2vec, in recovering communities for canonical network models with ground truth communities. Depending on the sparsity of the graph, we find the length of the random walk segments required such that the corresponding observed co-occurrence window is able to perform almost exact recovery of the underlying community assignments. We prove that, given some fixed co-occurrence window, node2vec using random walks with a low non-backtracking probability can succeed for much sparser networks compared to DeepWalk using simple random walks. Moreover, if the sparsity parameter is low, we provide evidence that these algorithms might not succeed in almost exact recovery. The analysis requires developing general tools for path counting on random networks having an underlying low-rank structure, which are of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge