On Graduated Optimization for Stochastic Non-Convex Problems

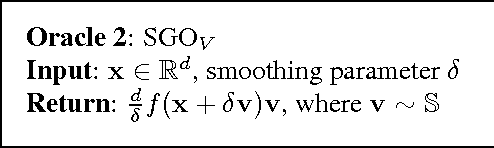
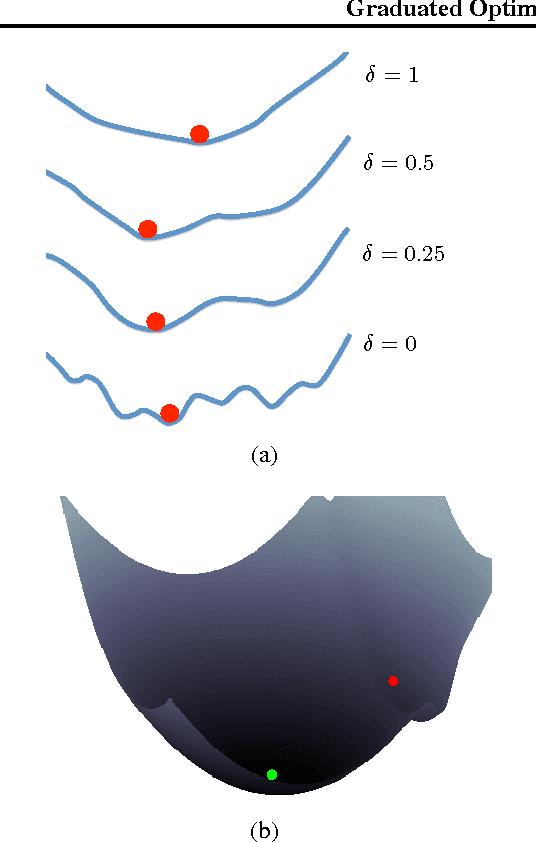
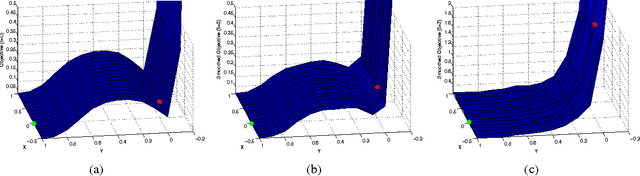
The graduated optimization approach, also known as the continuation method, is a popular heuristic to solving non-convex problems that has received renewed interest over the last decade. Despite its popularity, very little is known in terms of theoretical convergence analysis. In this paper we describe a new first-order algorithm based on graduated optimiza- tion and analyze its performance. We characterize a parameterized family of non- convex functions for which this algorithm provably converges to a global optimum. In particular, we prove that the algorithm converges to an {\epsilon}-approximate solution within O(1/\epsilon^2) gradient-based steps. We extend our algorithm and analysis to the setting of stochastic non-convex optimization with noisy gradient feedback, attaining the same convergence rate. Additionally, we discuss the setting of zero-order optimization, and devise a a variant of our algorithm which converges at rate of O(d^2/\epsilon^4).

Strongly Adaptive Online Learning

Strongly adaptive algorithms are algorithms whose performance on every time interval is close to optimal. We present a reduction that can transform standard low-regret algorithms to strongly adaptive. As a consequence, we derive simple, yet efficient, strongly adaptive algorithms for a handful of problems.

Faster SGD Using Sketched Conditioning

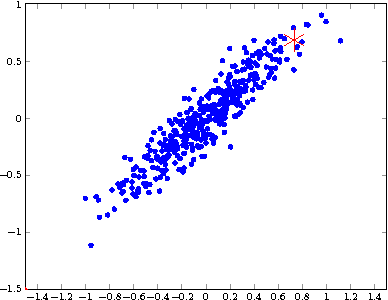
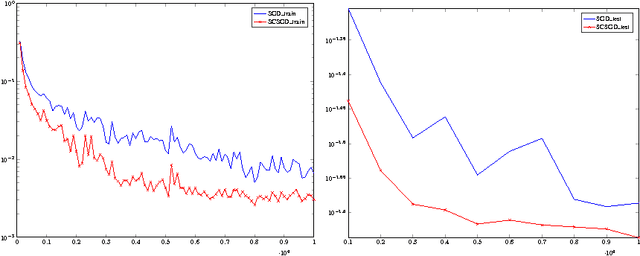
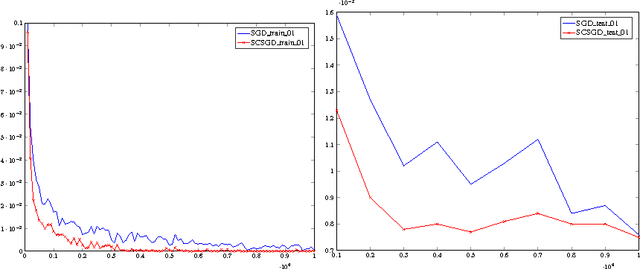
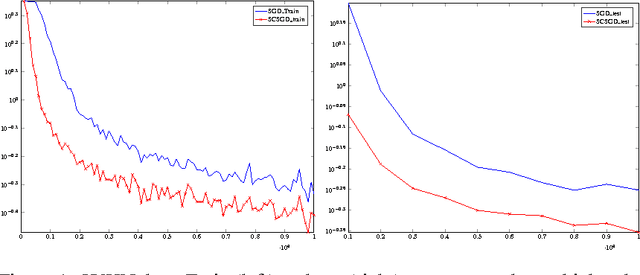
We propose a novel method for speeding up stochastic optimization algorithms via sketching methods, which recently became a powerful tool for accelerating algorithms for numerical linear algebra. We revisit the method of conditioning for accelerating first-order methods and suggest the use of sketching methods for constructing a cheap conditioner that attains a significant speedup with respect to the Stochastic Gradient Descent (SGD) algorithm. While our theoretical guarantees assume convexity, we discuss the applicability of our method to deep neural networks, and experimentally demonstrate its merits.

On Lower and Upper Bounds for Smooth and Strongly Convex Optimization Problems

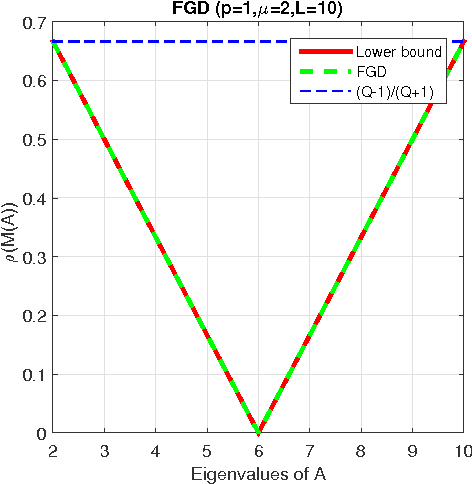
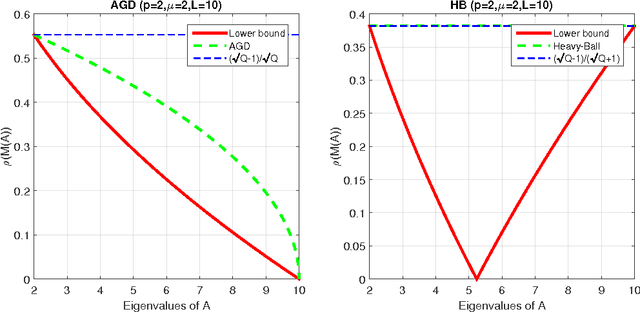
We develop a novel framework to study smooth and strongly convex optimization algorithms, both deterministic and stochastic. Focusing on quadratic functions we are able to examine optimization algorithms as a recursive application of linear operators. This, in turn, reveals a powerful connection between a class of optimization algorithms and the analytic theory of polynomials whereby new lower and upper bounds are derived. Whereas existing lower bounds for this setting are only valid when the dimensionality scales with the number of iterations, our lower bound holds in the natural regime where the dimensionality is fixed. Lastly, expressing it as an optimal solution for the corresponding optimization problem over polynomials, as formulated by our framework, we present a novel systematic derivation of Nesterov's well-known Accelerated Gradient Descent method. This rather natural interpretation of AGD contrasts with earlier ones which lacked a simple, yet solid, motivation.

SDCA without Duality

Stochastic Dual Coordinate Ascent is a popular method for solving regularized loss minimization for the case of convex losses. In this paper we show how a variant of SDCA can be applied for non-convex losses. We prove linear convergence rate even if individual loss functions are non-convex as long as the expected loss is convex.

Multiclass learnability and the ERM principle

We study the sample complexity of multiclass prediction in several learning settings. For the PAC setting our analysis reveals a surprising phenomenon: In sharp contrast to binary classification, we show that there exist multiclass hypothesis classes for which some Empirical Risk Minimizers (ERM learners) have lower sample complexity than others. Furthermore, there are classes that are learnable by some ERM learners, while other ERM learners will fail to learn them. We propose a principle for designing good ERM learners, and use this principle to prove tight bounds on the sample complexity of learning {\em symmetric} multiclass hypothesis classes---classes that are invariant under permutations of label names. We further provide a characterization of mistake and regret bounds for multiclass learning in the online setting and the bandit setting, using new generalizations of Littlestone's dimension.

On the Computational Efficiency of Training Neural Networks

It is well-known that neural networks are computationally hard to train. On the other hand, in practice, modern day neural networks are trained efficiently using SGD and a variety of tricks that include different activation functions (e.g. ReLU), over-specification (i.e., train networks which are larger than needed), and regularization. In this paper we revisit the computational complexity of training neural networks from a modern perspective. We provide both positive and negative results, some of them yield new provably efficient and practical algorithms for training certain types of neural networks.

Optimal Learners for Multiclass Problems

The fundamental theorem of statistical learning states that for binary classification problems, any Empirical Risk Minimization (ERM) learning rule has close to optimal sample complexity. In this paper we seek for a generic optimal learner for multiclass prediction. We start by proving a surprising result: a generic optimal multiclass learner must be improper, namely, it must have the ability to output hypotheses which do not belong to the hypothesis class, even though it knows that all the labels are generated by some hypothesis from the class. In particular, no ERM learner is optimal. This brings back the fundmamental question of "how to learn"? We give a complete answer to this question by giving a new analysis of the one-inclusion multiclass learner of Rubinstein et al (2006) showing that its sample complexity is essentially optimal. Then, we turn to study the popular hypothesis class of generalized linear classifiers. We derive optimal learners that, unlike the one-inclusion algorithm, are computationally efficient. Furthermore, we show that the sample complexity of these learners is better than the sample complexity of the ERM rule, thus settling in negative an open question due to Collins (2005).

The complexity of learning halfspaces using generalized linear methods

Many popular learning algorithms (E.g. Regression, Fourier-Transform based algorithms, Kernel SVM and Kernel ridge regression) operate by reducing the problem to a convex optimization problem over a vector space of functions. These methods offer the currently best approach to several central problems such as learning half spaces and learning DNF's. In addition they are widely used in numerous application domains. Despite their importance, there are still very few proof techniques to show limits on the power of these algorithms. We study the performance of this approach in the problem of (agnostically and improperly) learning halfspaces with margin $\gamma$. Let $\mathcal{D}$ be a distribution over labeled examples. The $\gamma$-margin error of a hyperplane $h$ is the probability of an example to fall on the wrong side of $h$ or at a distance $\le\gamma$ from it. The $\gamma$-margin error of the best $h$ is denoted $\mathrm{Err}_\gamma(\mathcal{D})$. An $\alpha(\gamma)$-approximation algorithm receives $\gamma,\epsilon$ as input and, using i.i.d. samples of $\mathcal{D}$, outputs a classifier with error rate $\le \alpha(\gamma)\mathrm{Err}_\gamma(\mathcal{D}) + \epsilon$. Such an algorithm is efficient if it uses $\mathrm{poly}(\frac{1}{\gamma},\frac{1}{\epsilon})$ samples and runs in time polynomial in the sample size. The best approximation ratio achievable by an efficient algorithm is $O\left(\frac{1/\gamma}{\sqrt{\log(1/\gamma)}}\right)$ and is achieved using an algorithm from the above class. Our main result shows that the approximation ratio of every efficient algorithm from this family must be $\ge \Omega\left(\frac{1/\gamma}{\mathrm{poly}\left(\log\left(1/\gamma\right)\right)}\right)$, essentially matching the best known upper bound.

From average case complexity to improper learning complexity

The basic problem in the PAC model of computational learning theory is to determine which hypothesis classes are efficiently learnable. There is presently a dearth of results showing hardness of learning problems. Moreover, the existing lower bounds fall short of the best known algorithms. The biggest challenge in proving complexity results is to establish hardness of {\em improper learning} (a.k.a. representation independent learning).The difficulty in proving lower bounds for improper learning is that the standard reductions from $\mathbf{NP}$-hard problems do not seem to apply in this context. There is essentially only one known approach to proving lower bounds on improper learning. It was initiated in (Kearns and Valiant 89) and relies on cryptographic assumptions. We introduce a new technique for proving hardness of improper learning, based on reductions from problems that are hard on average. We put forward a (fairly strong) generalization of Feige's assumption (Feige 02) about the complexity of refuting random constraint satisfaction problems. Combining this assumption with our new technique yields far reaching implications. In particular, 1. Learning $\mathrm{DNF}$'s is hard. 2. Agnostically learning halfspaces with a constant approximation ratio is hard. 3. Learning an intersection of $\omega(1)$ halfspaces is hard.