When Hardness of Approximation Meets Hardness of Learning

A supervised learning algorithm has access to a distribution of labeled examples, and needs to return a function (hypothesis) that correctly labels the examples. The hypothesis of the learner is taken from some fixed class of functions (e.g., linear classifiers, neural networks etc.). A failure of the learning algorithm can occur due to two possible reasons: wrong choice of hypothesis class (hardness of approximation), or failure to find the best function within the hypothesis class (hardness of learning). Although both approximation and learnability are important for the success of the algorithm, they are typically studied separately. In this work, we show a single hardness property that implies both hardness of approximation using linear classes and shallow networks, and hardness of learning using correlation queries and gradient-descent. This allows us to obtain new results on hardness of approximation and learnability of parity functions, DNF formulas and $AC^0$ circuits.

On the Ethics of Building AI in a Responsible Manner

The AI-alignment problem arises when there is a discrepancy between the goals that a human designer specifies to an AI learner and a potential catastrophic outcome that does not reflect what the human designer really wants. We argue that a formalism of AI alignment that does not distinguish between strategic and agnostic misalignments is not useful, as it deems all technology as un-safe. We propose a definition of a strategic-AI-alignment and prove that most machine learning algorithms that are being used in practice today do not suffer from the strategic-AI-alignment problem. However, without being careful, today's technology might lead to strategic misalignment.

Proving the Lottery Ticket Hypothesis: Pruning is All You Need

The lottery ticket hypothesis (Frankle and Carbin, 2018), states that a randomly-initialized network contains a small subnetwork such that, when trained in isolation, can compete with the performance of the original network. We prove an even stronger hypothesis (as was also conjectured in Ramanujan et al., 2019), showing that for every bounded distribution and every target network with bounded weights, a sufficiently over-parameterized neural network with random weights contains a subnetwork with roughly the same accuracy as the target network, without any further training.

Learning Boolean Circuits with Neural Networks

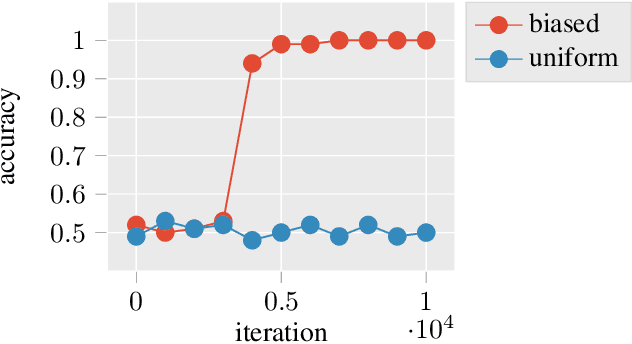
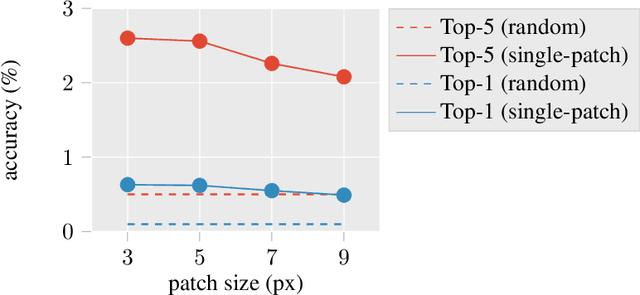
Training neural-networks is computationally hard. However, in practice they are trained efficiently using gradient-based algorithms, achieving remarkable performance on natural data. To bridge this gap, we observe the property of local correlation: correlation between small patterns of the input and the target label. We focus on learning deep neural-networks with a variant of gradient-descent, when the target function is a tree-structured Boolean circuit. We show that in this case, the existence of correlation between the gates of the circuit and the target label determines whether the optimization succeeds or fails. Using this result, we show that neural-networks can learn the (log n)-parity problem for most product distributions. These results hint that local correlation may play an important role in differentiating between distributions that are hard or easy to learn.

The Implicit Bias of Depth: How Incremental Learning Drives Generalization

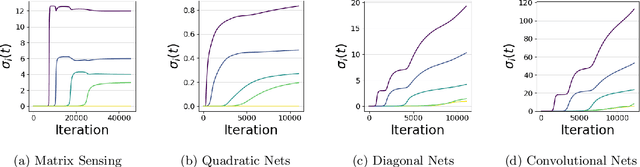
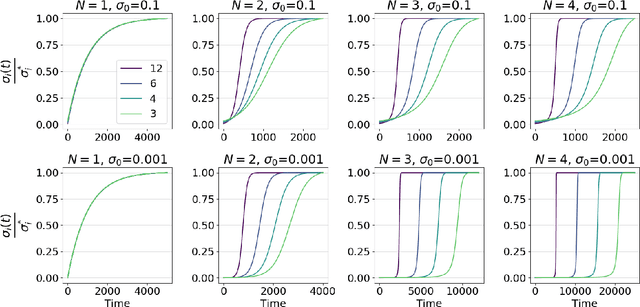
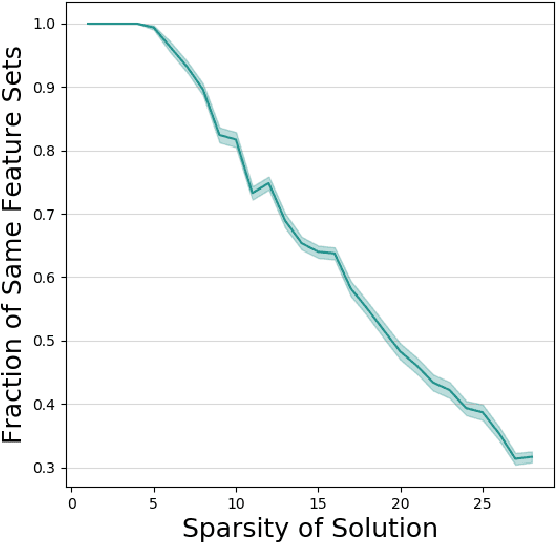
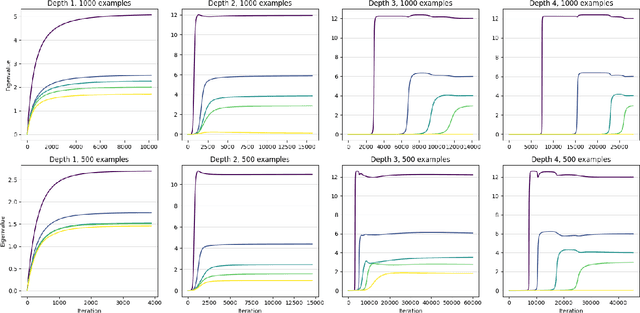
A leading hypothesis for the surprising generalization of neural networks is that the dynamics of gradient descent bias the model towards simple solutions, by searching through the solution space in an incremental order of complexity. We formally define the notion of incremental learning dynamics and derive the conditions on depth and initialization for which this phenomenon arises in deep linear models. Our main theoretical contribution is a dynamical depth separation result, proving that while shallow models can exhibit incremental learning dynamics, they require the initialization to be exponentially small for these dynamics to present themselves. However, once the model becomes deeper, the dependence becomes polynomial and incremental learning can arise in more natural settings. We complement our theoretical findings by experimenting with deep matrix sensing, quadratic neural networks and with binary classification using diagonal and convolutional linear networks, showing all of these models exhibit incremental learning.

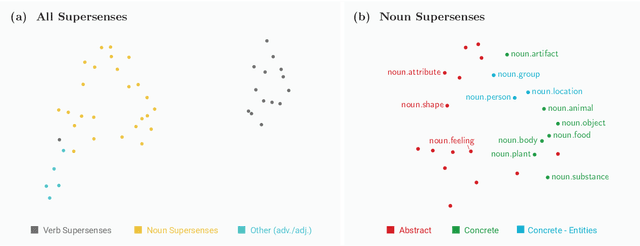
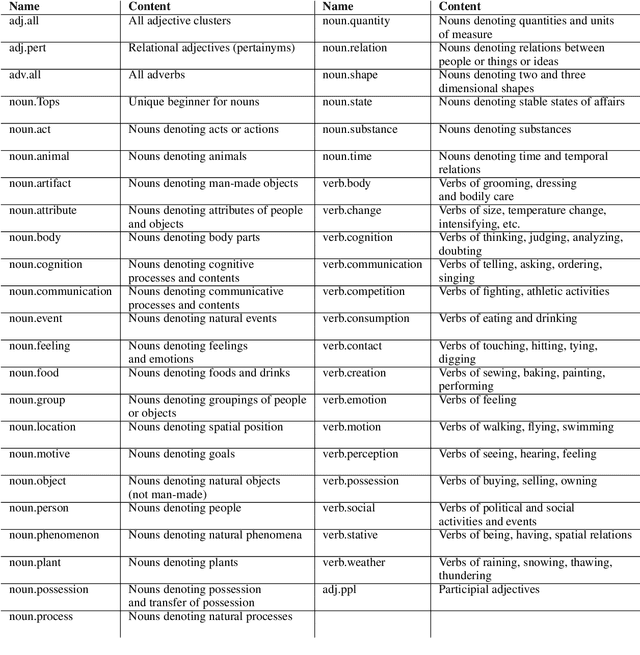
SenseBERT: Driving Some Sense into BERT

Self-supervision techniques have allowed neural language models to advance the frontier in Natural Language Understanding. However, existing self-supervision techniques operate at the word-form level, which serves as a surrogate for the underlying semantic content. This paper proposes a method to employ self-supervision directly at the word-sense level. Our model, named SenseBERT, is pre-trained to predict not only the masked words but also their WordNet supersenses. Accordingly, we attain a lexical-semantic level language model, without the use of human annotation. SenseBERT achieves significantly improved lexical understanding, as we demonstrate by experimenting on SemEval, and by attaining a state of the art result on the Word in Context (WiC) task. Our approach is extendable to other linguistic signals, which can be similarly integrated into the pre-training process, leading to increasingly semantically informed language models.

Discriminative Active Learning

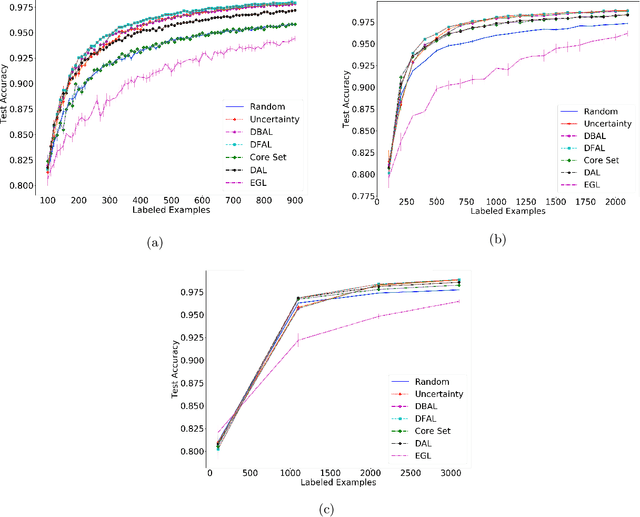
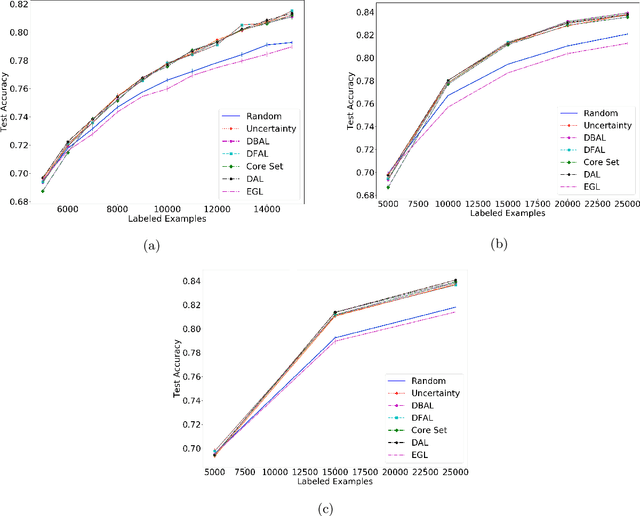
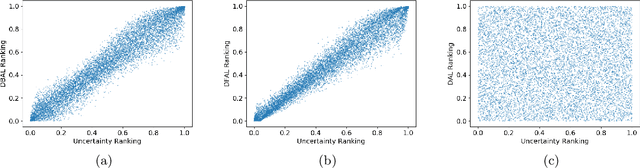
We propose a new batch mode active learning algorithm designed for neural networks and large query batch sizes. The method, Discriminative Active Learning (DAL), poses active learning as a binary classification task, attempting to choose examples to label in such a way as to make the labeled set and the unlabeled pool indistinguishable. Experimenting on image classification tasks, we empirically show our method to be on par with state of the art methods in medium and large query batch sizes, while being simple to implement and also extend to other domains besides classification tasks. Our experiments also show that none of the state of the art methods of today are clearly better than uncertainty sampling when the batch size is relatively large, negating some of the reported results in the recent literature.

Decoupling Gating from Linearity

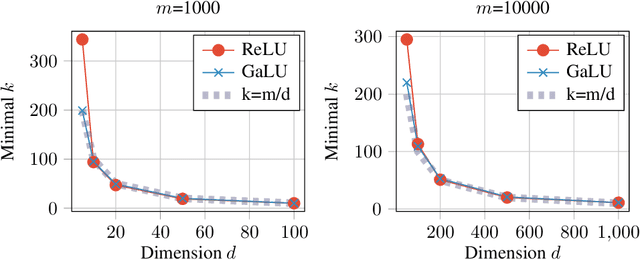
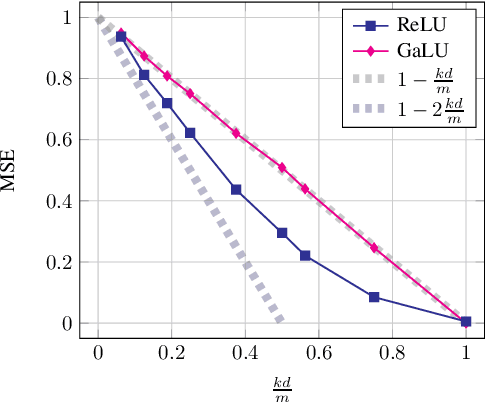
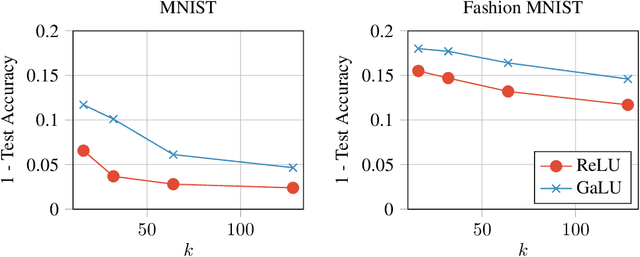
ReLU neural-networks have been in the focus of many recent theoretical works, trying to explain their empirical success. Nonetheless, there is still a gap between current theoretical results and empirical observations, even in the case of shallow (one hidden-layer) networks. For example, in the task of memorizing a random sample of size $m$ and dimension $d$, the best theoretical result requires the size of the network to be $\tilde{\Omega}(\frac{m^2}{d})$, while empirically a network of size slightly larger than $\frac{m}{d}$ is sufficient. To bridge this gap, we turn to study a simplified model for ReLU networks. We observe that a ReLU neuron is a product of a linear function with a gate (the latter determines whether the neuron is active or not), where both share a jointly trained weight vector. In this spirit, we introduce the Gated Linear Unit (GaLU), which simply decouples the linearity from the gating by assigning different vectors for each role. We show that GaLU networks allow us to get optimization and generalization results that are much stronger than those available for ReLU networks. Specifically, we show a memorization result for networks of size $\tilde{\Omega}(\frac{m}{d})$, and improved generalization bounds. Finally, we show that in some scenarios, GaLU networks behave similarly to ReLU networks, hence proving to be a good choice of a simplified model.

Is Deeper Better only when Shallow is Good?

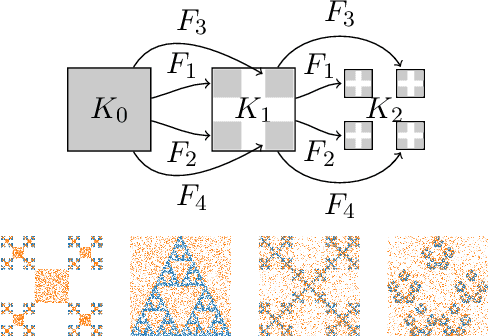
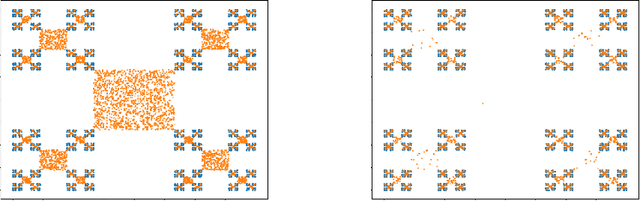
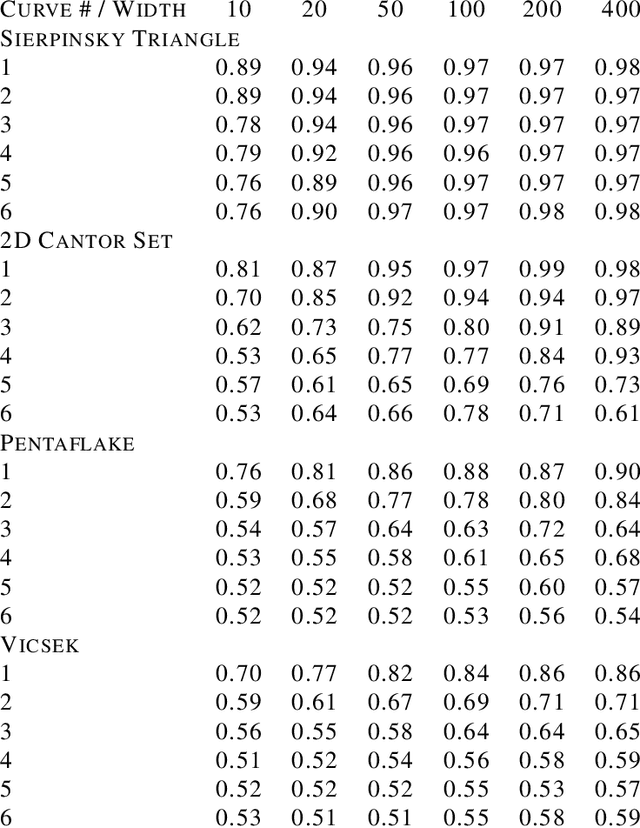
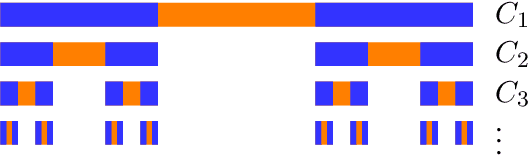
Understanding the power of depth in feed-forward neural networks is an ongoing challenge in the field of deep learning theory. While current works account for the importance of depth for the expressive power of neural-networks, it remains an open question whether these benefits are exploited during a gradient-based optimization process. In this work we explore the relation between expressivity properties of deep networks and the ability to train them efficiently using gradient-based algorithms. We give a depth separation argument for distributions with fractal structure, showing that they can be expressed efficiently by deep networks, but not with shallow ones. These distributions have a natural coarse-to-fine structure, and we show that the balance between the coarse and fine details has a crucial effect on whether the optimization process is likely to succeed. We prove that when the distribution is concentrated on the fine details, gradient-based algorithms are likely to fail. Using this result we prove that, at least in some distributions, the success of learning deep networks depends on whether the distribution can be well approximated by shallower networks, and we conjecture that this property holds in general.

Vision Zero: on a Provable Method for Eliminating Roadway Accidents without Compromising Traffic Throughput

We propose an economical, viable, approach to eliminate almost all car accidents. Our method relies on a mathematical model of safety and can be applied to all modern cars at a mild cost.