Locking-Free Training of Physics-Informed Neural Network for Solving Nearly Incompressible Elasticity Equations

Due to divergence instability, the accuracy of low-order conforming finite element methods for nearly incompressible homogeneous elasticity equations deteriorates as the Lam\'e coefficient $\lambda\to\infty$, or equivalently as the Poisson ratio $\nu\to1/2$. This phenomenon, known as locking or non-robustness, remains not fully understood despite extensive investigation. In this paper, we propose a robust method based on a fundamentally different, machine-learning-driven approach. Leveraging recently developed Physics-Informed Neural Networks (PINNs), we address the numerical solution of linear elasticity equations governing nearly incompressible materials. The core idea of our method is to appropriately decompose the given equations to alleviate the extreme imbalance in the coefficients, while simultaneously solving both the forward and inverse problems to recover the solutions of the decomposed systems as well as the associated external conditions. Through various numerical experiments, including constant, variable and parametric Lam\'e coefficients, we illustrate the efficiency of the proposed methodology.

Engineering application of physics-informed neural networks for Saint-Venant torsion

The Saint-Venant torsion theory is a classical theory for analyzing the torsional behavior of structural components, and it remains critically important in modern computational design workflows. Conventional numerical methods, including the finite element method (FEM), typically rely on mesh-based approaches to obtain approximate solutions. However, these methods often require complex and computationally intensive techniques to overcome the limitations of approximation, leading to significant increases in computational cost. The objective of this study is to develop a series of novel numerical methods based on physics-informed neural networks (PINN) for solving the Saint-Venant torsion equations. Utilizing the expressive power and the automatic differentiation capability of neural networks, the PINN can solve partial differential equations (PDEs) along with boundary conditions without the need for intricate computational techniques. First, a PINN solver was developed to compute the torsional constant for bars with arbitrary cross-sectional geometries. This was followed by the development of a solver capable of handling cases with sharp geometric transitions; variable-scaling PINN (VS-PINN). Finally, a parametric PINN was constructed to address the limitations of conventional single-instance PINN. The results from all three solvers showed good agreement with reference solutions, demonstrating their accuracy and robustness. Each solver can be selectively utilized depending on the specific requirements of torsional behavior analysis.

VS-PINN: A Fast and efficient training of physics-informed neural networks using variable-scaling methods for solving PDEs with stiff behavior

Physics-informed neural networks (PINNs) have recently emerged as a promising way to compute the solutions of partial differential equations (PDEs) using deep neural networks. However, despite their significant success in various fields, it remains unclear in many aspects how to effectively train PINNs if the solutions of PDEs exhibit stiff behaviors or high frequencies. In this paper, we propose a new method for training PINNs using variable-scaling techniques. This method is simple and it can be applied to a wide range of problems including PDEs with rapidly-varying solutions. Throughout various numerical experiments, we will demonstrate the effectiveness of the proposed method for these problems and confirm that it can significantly improve the training efficiency and performance of PINNs. Furthermore, based on the analysis of the neural tangent kernel (NTK), we will provide theoretical evidence for this phenomenon and show that our methods can indeed improve the performance of PINNs.

Error analysis for finite element operator learning methods for solving parametric second-order elliptic PDEs

In this paper, we provide a theoretical analysis of a type of operator learning method without data reliance based on the classical finite element approximation, which is called the finite element operator network (FEONet). We first establish the convergence of this method for general second-order linear elliptic PDEs with respect to the parameters for neural network approximation. In this regard, we address the role of the condition number of the finite element matrix in the convergence of the method. Secondly, we derive an explicit error estimate for the self-adjoint case. For this, we investigate some regularity properties of the solution in certain function classes for a neural network approximation, verifying the sufficient condition for the solution to have the desired regularity. Finally, we will also conduct some numerical experiments that support the theoretical findings, confirming the role of the condition number of the finite element matrix in the overall convergence.

Finite Element Operator Network for Solving Parametric PDEs

Partial differential equations (PDEs) underlie our understanding and prediction of natural phenomena across numerous fields, including physics, engineering, and finance. However, solving parametric PDEs is a complex task that necessitates efficient numerical methods. In this paper, we propose a novel approach for solving parametric PDEs using a Finite Element Operator Network (FEONet). Our proposed method leverages the power of deep learning in conjunction with traditional numerical methods, specifically the finite element method, to solve parametric PDEs in the absence of any paired input-output training data. We demonstrate the effectiveness of our approach on several benchmark problems and show that it outperforms existing state-of-the-art methods in terms of accuracy, generalization, and computational flexibility. Our FEONet framework shows potential for application in various fields where PDEs play a crucial role in modeling complex domains with diverse boundary conditions and singular behavior. Furthermore, we provide theoretical convergence analysis to support our approach, utilizing finite element approximation in numerical analysis.

Convergence analysis of unsupervised Legendre-Galerkin neural networks for linear second-order elliptic PDEs

In this paper, we perform the convergence analysis of unsupervised Legendre--Galerkin neural networks (ULGNet), a deep-learning-based numerical method for solving partial differential equations (PDEs). Unlike existing deep learning-based numerical methods for PDEs, the ULGNet expresses the solution as a spectral expansion with respect to the Legendre basis and predicts the coefficients with deep neural networks by solving a variational residual minimization problem. Since the corresponding loss function is equivalent to the residual induced by the linear algebraic system depending on the choice of basis functions, we prove that the minimizer of the discrete loss function converges to the weak solution of the PDEs. Numerical evidence will also be provided to support the theoretical result. Key technical tools include the variant of the universal approximation theorem for bounded neural networks, the analysis of the stiffness and mass matrices, and the uniform law of large numbers in terms of the Rademacher complexity.

A novel approach for wafer defect pattern classification based on topological data analysis

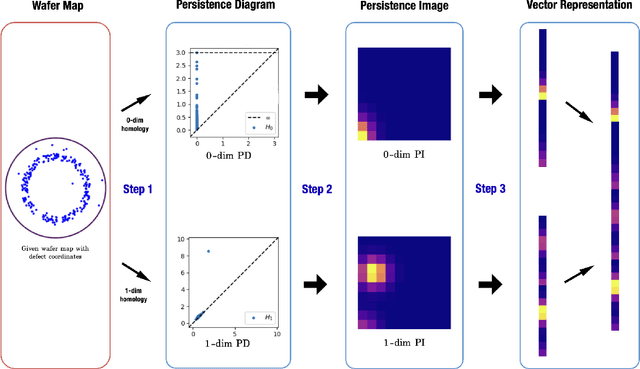
In semiconductor manufacturing, wafer map defect pattern provides critical information for facility maintenance and yield management, so the classification of defect patterns is one of the most important tasks in the manufacturing process. In this paper, we propose a novel way to represent the shape of the defect pattern as a finite-dimensional vector, which will be used as an input for a neural network algorithm for classification. The main idea is to extract the topological features of each pattern by using the theory of persistent homology from topological data analysis (TDA). Through some experiments with a simulated dataset, we show that the proposed method is faster and much more efficient in training with higher accuracy, compared with the method using convolutional neural networks (CNN) which is the most common approach for wafer map defect pattern classification. Moreover, our method outperforms the CNN-based method when the number of training data is not enough and is imbalanced.