The Best Arm Evades: Near-optimal Multi-pass Streaming Lower Bounds for Pure Exploration in Multi-armed Bandits

We give a near-optimal sample-pass trade-off for pure exploration in multi-armed bandits (MABs) via multi-pass streaming algorithms: any streaming algorithm with sublinear memory that uses the optimal sample complexity of $O(\frac{n}{\Delta^2})$ requires $\Omega(\frac{\log{(1/\Delta)}}{\log\log{(1/\Delta)}})$ passes. Here, $n$ is the number of arms and $\Delta$ is the reward gap between the best and the second-best arms. Our result matches the $O(\log(\frac{1}{\Delta}))$-pass algorithm of Jin et al. [ICML'21] (up to lower order terms) that only uses $O(1)$ memory and answers an open question posed by Assadi and Wang [STOC'20].

Sublinear Time and Space Algorithms for Correlation Clustering via Sparse-Dense Decompositions

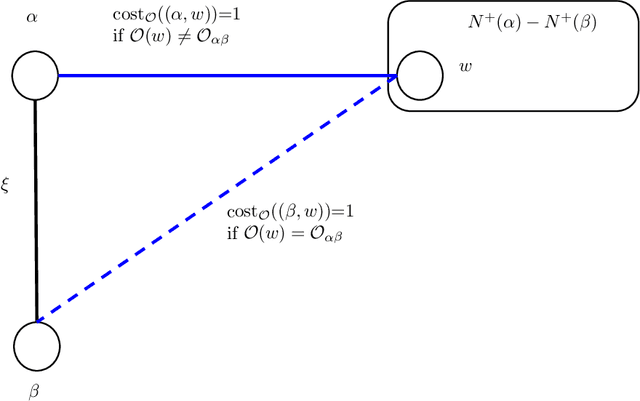
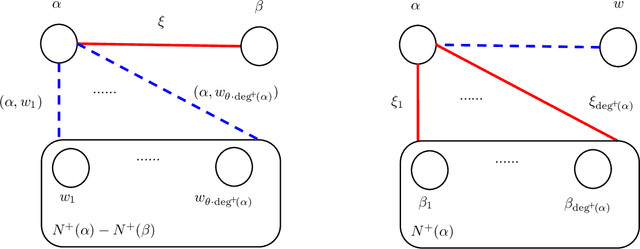
We present a new approach for solving (minimum disagreement) correlation clustering that results in sublinear algorithms with highly efficient time and space complexity for this problem. In particular, we obtain the following algorithms for $n$-vertex $(+/-)$-labeled graphs $G$: -- A sublinear-time algorithm that with high probability returns a constant approximation clustering of $G$ in $O(n\log^2{n})$ time assuming access to the adjacency list of the $(+)$-labeled edges of $G$ (this is almost quadratically faster than even reading the input once). Previously, no sublinear-time algorithm was known for this problem with any multiplicative approximation guarantee. -- A semi-streaming algorithm that with high probability returns a constant approximation clustering of $G$ in $O(n\log{n})$ space and a single pass over the edges of the graph $G$ (this memory is almost quadratically smaller than input size). Previously, no single-pass algorithm with $o(n^2)$ space was known for this problem with any approximation guarantee. The main ingredient of our approach is a novel connection to sparse-dense graph decompositions that are used extensively in the graph coloring literature. To our knowledge, this connection is the first application of these decompositions beyond graph coloring, and in particular for the correlation clustering problem, and can be of independent interest.

Exploration with Limited Memory: Streaming Algorithms for Coin Tossing, Noisy Comparisons, and Multi-Armed Bandits

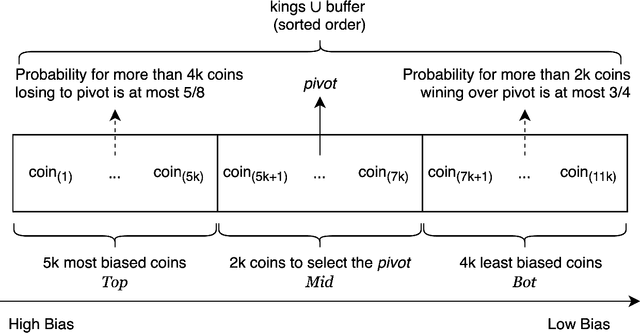
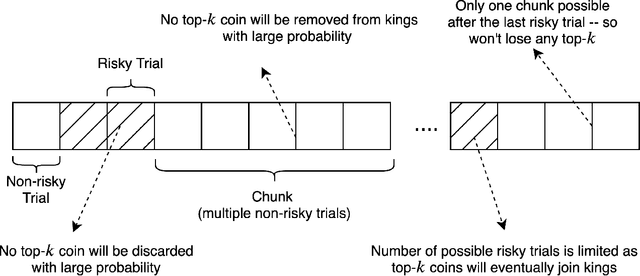
Consider the following abstract coin tossing problem: Given a set of $n$ coins with unknown biases, find the most biased coin using a minimal number of coin tosses. This is a common abstraction of various exploration problems in theoretical computer science and machine learning and has been studied extensively over the years. In particular, algorithms with optimal sample complexity (number of coin tosses) have been known for this problem for quite some time. Motivated by applications to processing massive datasets, we study the space complexity of solving this problem with optimal number of coin tosses in the streaming model. In this model, the coins are arriving one by one and the algorithm is only allowed to store a limited number of coins at any point -- any coin not present in the memory is lost and can no longer be tossed or compared to arriving coins. Prior algorithms for the coin tossing problem with optimal sample complexity are based on iterative elimination of coins which inherently require storing all the coins, leading to memory-inefficient streaming algorithms. We remedy this state-of-affairs by presenting a series of improved streaming algorithms for this problem: we start with a simple algorithm which require storing only $O(\log{n})$ coins and then iteratively refine it further and further, leading to algorithms with $O(\log\log{(n)})$ memory, $O(\log^*{(n)})$ memory, and finally a one that only stores a single extra coin in memory -- the same exact space needed to just store the best coin throughout the stream. Furthermore, we extend our algorithms to the problem of finding the $k$ most biased coins as well as other exploration problems such as finding top-$k$ elements using noisy comparisons or finding an $\epsilon$-best arm in stochastic multi-armed bandits, and obtain efficient streaming algorithms for these problems.