Dynamic DBSCAN with Euler Tour Sequences

We propose a fast and dynamic algorithm for Density-Based Spatial Clustering of Applications with Noise (DBSCAN) that efficiently supports online updates. Traditional DBSCAN algorithms, designed for batch processing, become computationally expensive when applied to dynamic datasets, particularly in large-scale applications where data continuously evolves. To address this challenge, our algorithm leverages the Euler Tour Trees data structure, enabling dynamic clustering updates without the need to reprocess the entire dataset. This approach preserves a near-optimal accuracy in density estimation, as achieved by the state-of-the-art static DBSCAN method (Esfandiari et al., 2021) Our method achieves an improved time complexity of $O(d \log^3(n) + \log^4(n))$ for every data point insertion and deletion, where $n$ and $d$ denote the total number of updates and the data dimension, respectively. Empirical studies also demonstrate significant speedups over conventional DBSCANs in real-time clustering of dynamic datasets, while maintaining comparable or superior clustering quality.

Transfer Learning in Bandits with Latent Continuity

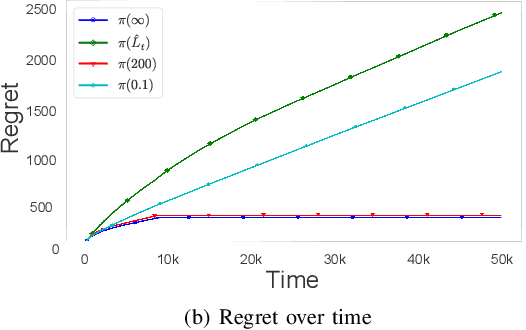
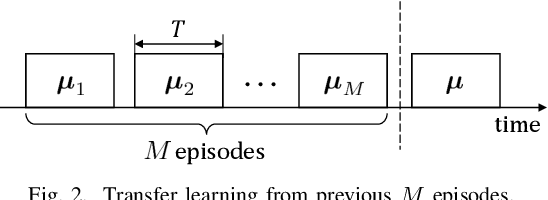
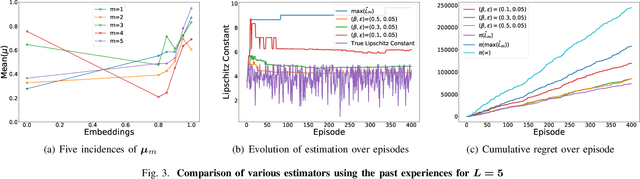
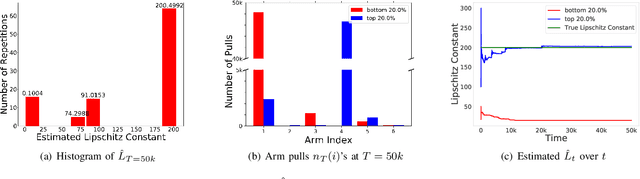
Structured stochastic multi-armed bandits provide accelerated regret rates over the standard unstructured bandit problems. Most structured bandits, however, assume the knowledge of the structural parameter such as Lipschitz continuity, which is often not available. To cope with the latent structural parameter, we consider a transfer learning setting in which an agent must learn to transfer the structural information from the prior tasks to the next task, which is inspired by practical problems such as rate adaptation in wireless link. We propose a novel framework to provably and accurately estimate the Lipschitz constant based on previous tasks and fully exploit it for the new task at hand. We analyze the efficiency of the proposed framework in two folds: (i) the sample complexity of our estimator matches with the information-theoretic fundamental limit; and (ii) our regret bound on the new task is close to that of the oracle algorithm with the full knowledge of the Lipschitz constant under mild assumptions. Our analysis reveals a set of useful insights on transfer learning for latent Lipschitzconstants such as the fundamental challenge a learner faces. Our numerical evaluations confirm our theoretical findings and show the superiority of the proposed framework compared to baselines.