Deep Learning How to Fit an Intravoxel Incoherent Motion Model to Diffusion-Weighted MRI

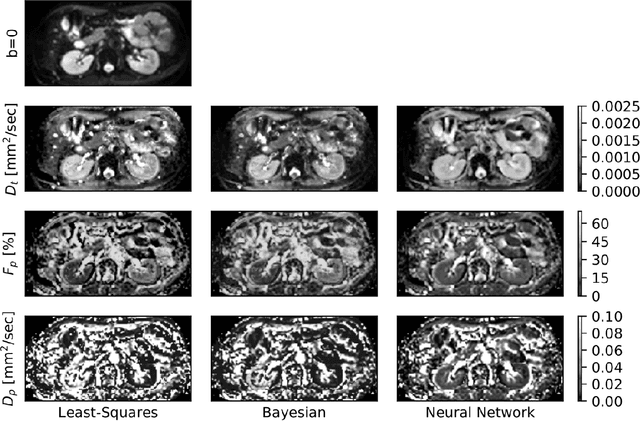
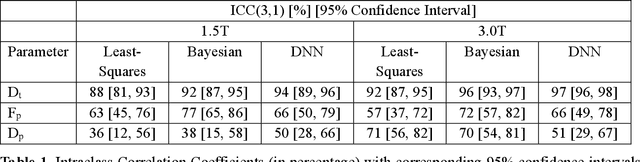
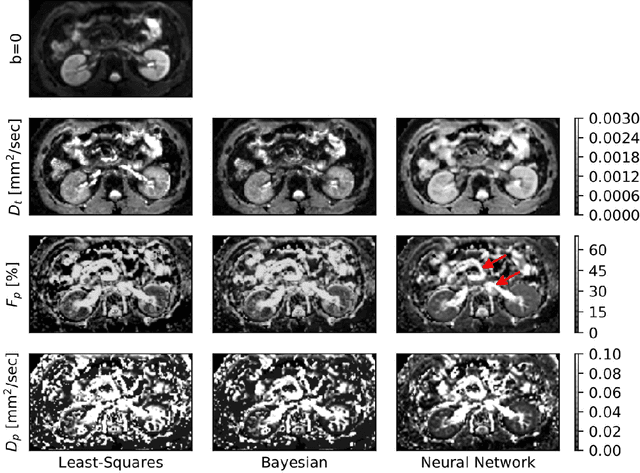
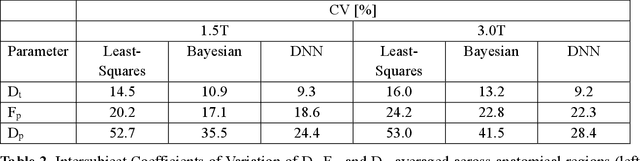
Purpose: This prospective clinical study assesses the feasibility of training a deep neural network (DNN) for intravoxel incoherent motion (IVIM) model fitting to diffusion-weighted magnetic resonance imaging (DW-MRI) data and evaluates its performance. Methods: Approval for this study was obtained by the responsible ethics committees and written informed consent was obtained from all accrued subjects. In May 2011, ten male volunteers (age range: 29 to 53 years, mean: 37 years) underwent DW-MRI of the upper abdomen on 1.5T and 3.0T magnetic resonance scanners. Regions of interest in the left and right liver lobe, pancreas, spleen, renal cortex, and renal medulla were delineated independently by two readers. DNNs were trained for IVIM model fitting using these data; results were compared to least-squares and Bayesian approaches to IVIM fitting. Intraclass Correlation Coefficients (ICC) were used to assess consistency of measurements between readers. Intersubject variability was evaluated using Coefficients of Variation (CV). The fitting error was calculated based on simulated data and the average fitting time of each method was recorded. Results: DNNs were trained successfully for IVIM parameter estimation. This approach was associated with high consistency between the two readers (ICCs between 50 and 97%), low intersubject variability of estimated parameter values (CVs between 9.2 and 28.4), and the lowest error when compared with least-squares and Bayesian approaches. Further, fitting by DNNs was several orders of magnitude quicker than the other methods. Conclusion: DNNs are recommended for accurate and robust IVIM model fitting to DW-MRI data. Suitable software is available at (1).

A Ray-based Approach for Boundary Estimation of Fiber Bundles Derived from Diffusion Tensor Imaging

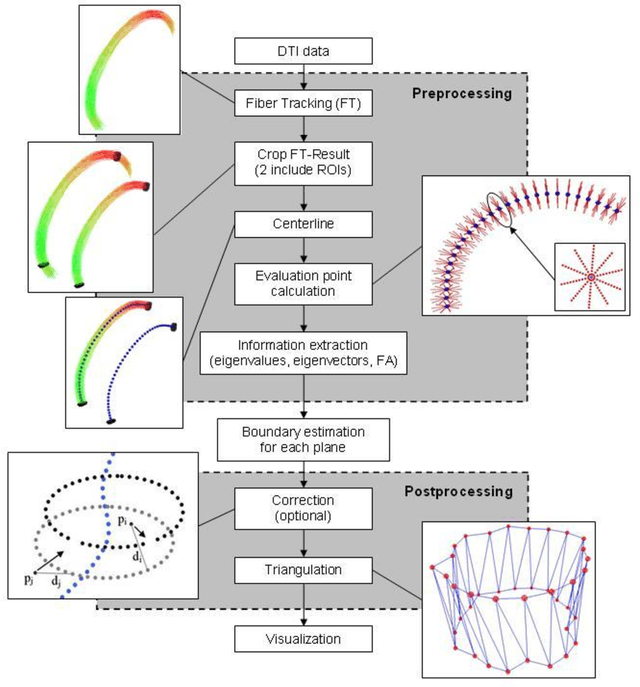
Diffusion Tensor Imaging (DTI) is a non-invasive imaging technique that allows estimation of the location of white matter tracts in-vivo, based on the measurement of water diffusion properties. For each voxel, a second-order tensor can be calculated by using diffusion-weighted sequences (DWI) that are sensitive to the random motion of water molecules. Given at least 6 diffusion-weighted images with different gradients and one unweighted image, the coefficients of the symmetric diffusion tensor matrix can be calculated. Deriving the eigensystem of the tensor, the eigenvectors and eigenvalues can be calculated to describe the three main directions of diffusion and its magnitude. Using DTI data, fiber bundles can be determined, to gain information about eloquent brain structures. Especially in neurosurgery, information about location and dimension of eloquent structures like the corticospinal tract or the visual pathways is of major interest. Therefore, the fiber bundle boundary has to be determined. In this paper, a novel ray-based approach for boundary estimation of tubular structures is presented.

Benchmarking the Quality of Diffusion-Weighted Images

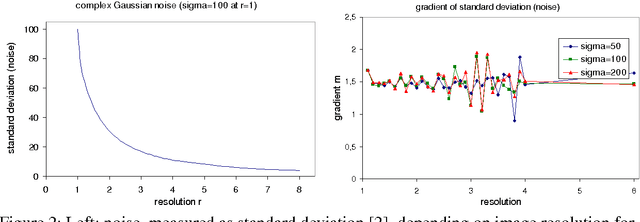
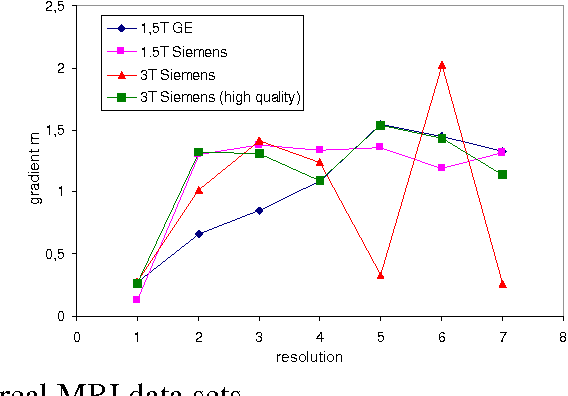
We present a novel method that allows for measuring the quality of diffusion-weighted MR images dependent on the image resolution and the image noise. For this purpose, we introduce a new thresholding technique so that noise and the signal can automatically be estimated from a single data set. Thus, no user interaction as well as no double acquisition technique, which requires a time-consuming proper geometrical registration, is needed. As a coarser image resolution or slice thickness leads to a higher signal-to-noise ratio (SNR), our benchmark determines a resolution-independent quality measure so that images with different resolutions can be adequately compared. To evaluate our method, a set of diffusion-weighted images from different vendors is used. It is shown that the quality can efficiently be determined and that the automatically computed SNR is comparable to the SNR which is measured manually in a manually selected region of interest.

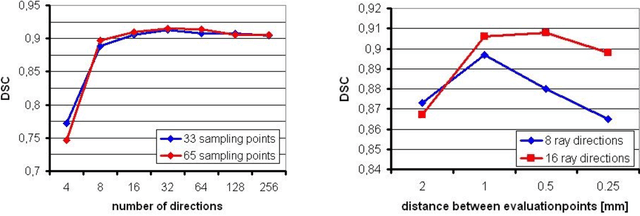
Ray-Based and Graph-Based Methods for Fiber Bundle Boundary Estimation

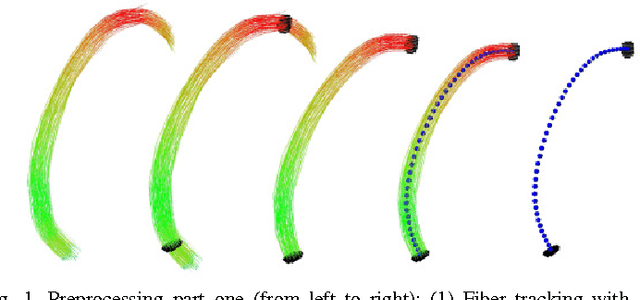
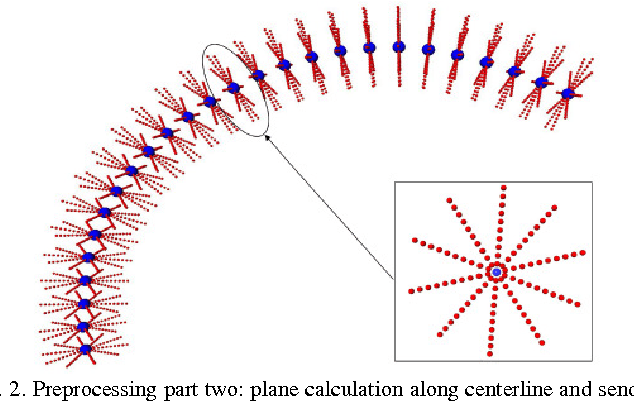
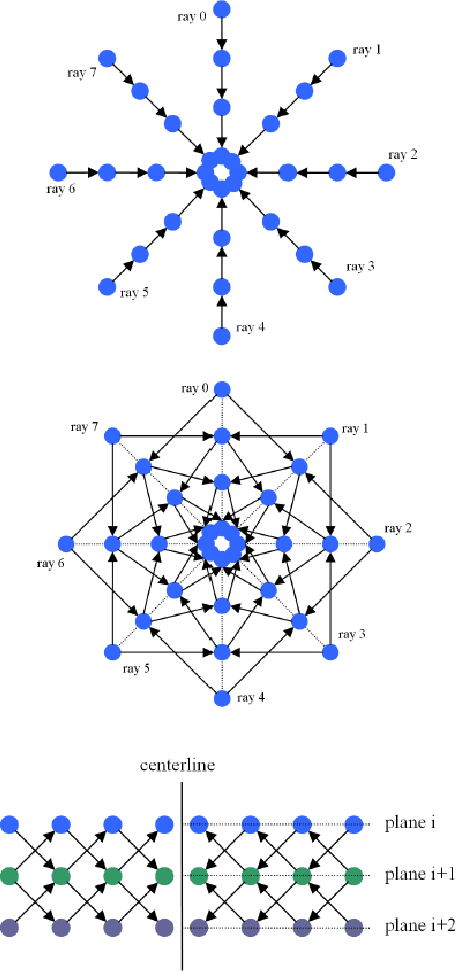
Diffusion Tensor Imaging (DTI) provides the possibility of estimating the location and course of eloquent structures in the human brain. Knowledge about this is of high importance for preoperative planning of neurosurgical interventions and for intraoperative guidance by neuronavigation in order to minimize postoperative neurological deficits. Therefore, the segmentation of these structures as closed, three-dimensional object is necessary. In this contribution, two methods for fiber bundle segmentation between two defined regions are compared using software phantoms (abstract model and anatomical phantom modeling the right corticospinal tract). One method uses evaluation points from sampled rays as candidates for boundary points, the other method sets up a directed and weighted (depending on a scalar measure) graph and performs a min-cut for optimal segmentation results. Comparison is done by using the Dice Similarity Coefficient (DSC), a measure for spatial overlap of different segmentation results.

A Semi-Automatic Graph-Based Approach for Determining the Boundary of Eloquent Fiber Bundles in the Human Brain

Diffusion Tensor Imaging (DTI) allows estimating the position, orientation and dimension of bundles of nerve pathways. This non-invasive imaging technique takes advantage of the diffusion of water molecules and determines the diffusion coefficients for every voxel of the data set. The identification of the diffusion coefficients and the derivation of information about fiber bundles is of major interest for planning and performing neurosurgical interventions. To minimize the risk of neural deficits during brain surgery as tumor resection (e.g. glioma), the segmentation and integration of the results in the operating room is of prime importance. In this contribution, a robust and efficient graph-based approach for segmentating tubular fiber bundles in the human brain is presented. To define a cost function, the fractional anisotropy (FA) is used, derived from the DTI data, but this value may differ from patient to patient. Besides manually definining seed regions describing the structure of interest, additionally a manual definition of the cost function by the user is necessary. To improve the approach the contribution introduces a solution for automatically determining the cost function by using different 3D masks for each individual data set.