Denoising and Reconstruction of Nonlinear Dynamics using Truncated Reservoir Computing

Measurements acquired from distributed physical systems are often sparse and noisy. Therefore, signal processing and system identification tools are required to mitigate noise effects and reconstruct unobserved dynamics from limited sensor data. However, this process is particularly challenging because the fundamental equations governing the dynamics are largely unavailable in practice. Reservoir Computing (RC) techniques have shown promise in efficiently simulating dynamical systems through an unstructured and efficient computation graph comprising a set of neurons with random connectivity. However, the potential of RC to operate in noisy regimes and distinguish noise from the primary dynamics of the system has not been fully explored. This paper presents a novel RC method for noise filtering and reconstructing nonlinear dynamics, offering a novel learning protocol associated with hyperparameter optimization. The performance of the RC in terms of noise intensity, noise frequency content, and drastic shifts in dynamical parameters are studied in two illustrative examples involving the nonlinear dynamics of the Lorenz attractor and adaptive exponential integrate-and-fire system (AdEx). It is shown that the denoising performance improves via truncating redundant nodes and edges of the computing reservoir, as well as properly optimizing the hyperparameters, e.g., the leakage rate, the spectral radius, the input connectivity, and the ridge regression parameter. Furthermore, the presented framework shows good generalization behavior when tested for reconstructing unseen attractors from the bifurcation diagram. Compared to the Extended Kalman Filter (EKF), the presented RC framework yields competitive accuracy at low signal-to-noise ratios (SNRs) and high-frequency ranges.

Deep learning for brake squeal: vibration detection, characterization and prediction

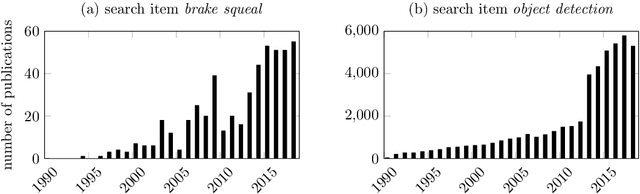
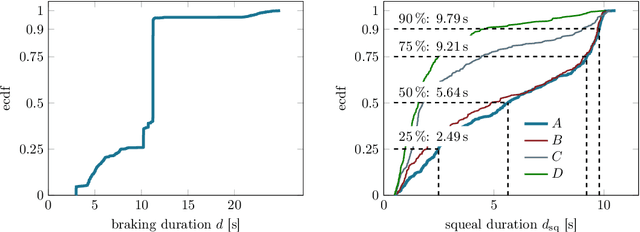
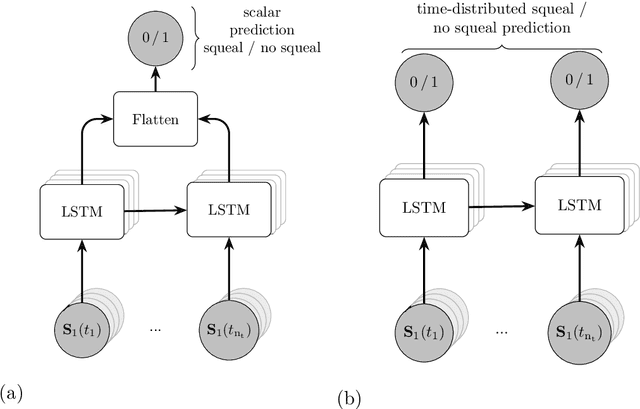
Despite significant advances in numerical modeling of brake squeal, the majority of industrial research and design is still conducted experimentally. In this work we report on novel strategies for handling data-intensive vibration testings and gaining better insights into brake system vibrations. To this end, we propose machine learning-based methods to detect and characterize vibrations, understand sensitivities and predict brake squeal. Our aim is to illustrate how interdisciplinary approaches can leverage the potential of data science techniques for classical mechanical engineering challenges. In the first part, a deep learning brake squeal detector is developed to identify several classes of typical sounds in vibration recordings. The detection method is rooted in recent computer vision techniques for object detection. It allows to overcome limitations of classical approaches that rely on spectral properties of the recorded vibrations. Results indicate superior detection and characterization quality when compared to state-of-the-art brake squeal detectors. In the second part, deep recurrent neural networks are employed to learn the parametric patterns that determine the dynamic stability of the brake system during operation. Given a set of multivariate loading conditions, the models learn to predict the vibrational behavior of the structure. The validated models represent virtual twins for the squeal behavior of a specific brake system. It is found that those models can predict the occurrence and onset of brake squeal with high accuracy. Hence, the deep learning models can identify the complicated patterns and temporal dependencies in the loading conditions that drive the dynamical structure into regimes of instability. Large data sets from commercial brake system testing are used to train and validate the deep learning models.